3. Расчет математического ожидания и среднеквадратического отклонения сигнала ошибки
Замена нелинейного звена линеаризованной моделью позволяет использовать принцип суперпозиции - провести раздельный анализ преобразования системой детерминированных и случайных составляющих входных сигналов. Особенность применения принципа суперпозиции на основе статистической линеаризации состоит в том, что для случайных составляющих нелинейное звено заменяется безынерционным звеном с коэффициентом k1, а для детерминированных - безынерционным звеном с коэффициентом k0 (при нечетной нелинейности) или постоянным сигналом 0.
Определяемые по полученным выше формулам коэффициенты статистической линеаризации оказываются функциями моментов распределения сигналов на входе нелинейности, которые, в свою очередь, вычисляются через передаточные функции системы, включающей в себя линеаризованное звено, то есть зависят от коэффициентов статистической линеаризации. Вследствие этого расчет стационарного процесса в статистически линеаризованной системе сводится к решению системы нелинейных алгебраических уравнений, требующему применения численных методов.
Для заданной системы (рисунок 1) передаточная функция линейной части:
.
Задающее воздействие
изменяется по закону g(t)=g1(t).
На входе действует случайная помеха
F(t)
с нулевым математическим ожиданием и
спектральной плотностью
.
Требуется определить математическое
ожидание и среднеквадратическое
отклонение сигнала ошибки в установившемся
процессе.
Выделим
детерминированную и случайную составляющие
сигнала ошибки:
.
С учетом характера входных сигналов и
в соответствии с принципом суперпозиции
составляющие сигнала ошибки в
линеаризованной системе будут определяться
следующим образом:
mx(t)=
xgуст,
.
Для расчета детерминированной составляющей сигнала ошибки после линеаризации используется структурная схема (рис. 4,а), а для расчета центрированной случайной составляющей - структурная схема (рис. 4,б), где
,
=k1(mx,σx).
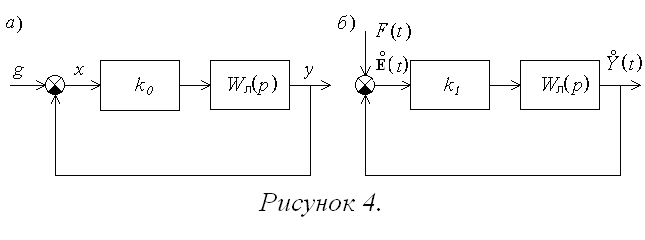
Для полученных структурных схем искомые характеристики сигнала ошибки определяются следующим образом: mE=mx, DE=DY.
При расчете детерминированной составляющей передаточная функция замкнутой системы по ошибке имеет вид:
.
В результате:
.
Среднеквадратическое отклонение сигнала ошибки в рассматриваемой задаче полностью определяется возмущающим воздействием и находится через дисперсию выходного сигнала и передаточную функцию замкнутой системы по возмущению, которая в рассматриваемом примере примет вид:
.
В результате:
,
Коэффициенты полиномов (1) примут вид:
a0=T1T2,
,
,
,
b0=0,
b1=0,
.
Определители (3) будут иметь третий порядок и получаются следующими:
=
.
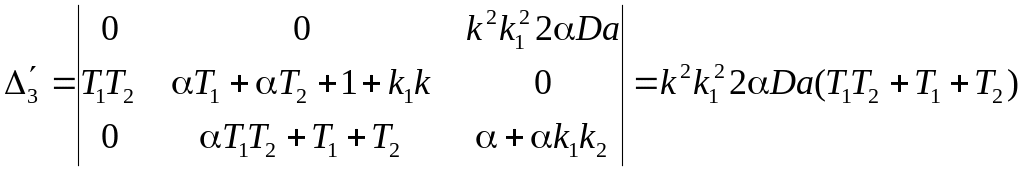В результате:
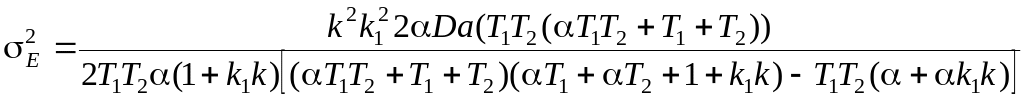
При заданных k, T и c для расчета характеристик ошибки необходимо решить систему нелинейных алгебраических уравнений:
mE=
,
,
,
.
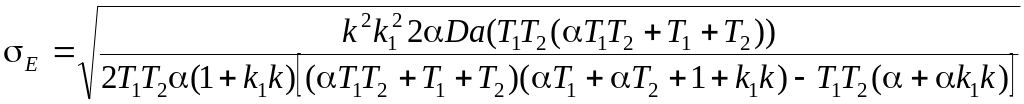4. РЕШЕНИЕ УРАВНЕНИЙ И ПОСТРОЕНИЕ ЗАВИСИМОСТЕЙ
С помощью программы, написанной на языке MATLAB, решив систему методом последовательных приближений, мы найдем зависимости коэффициентов статистической линеаризации, математического ожидания и среднеквадратического отклонения ошибки системы E(t) от величины коэффициента передачи k. Для нахождения зависимости M от k использована функция MATLAB fzero. Текст программы представлен в приложении А. Графики зависимостей представлены на рисунках 5-9.
Рисунок 5
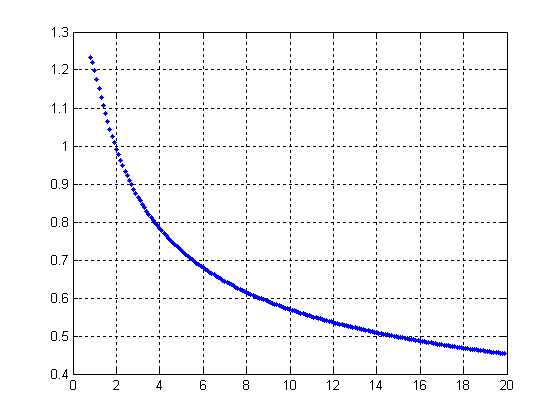
Рисунок 6
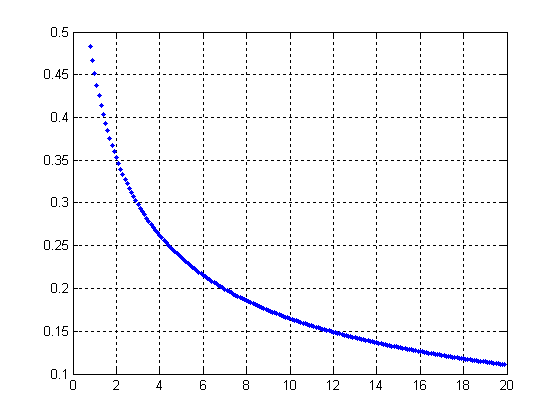
Рисунок 7
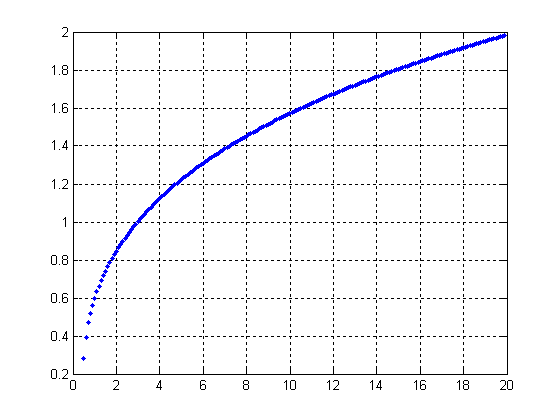
Рисунок 8
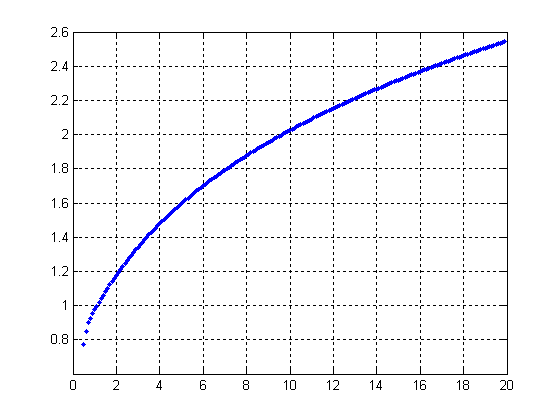
Рисунок 9