9.7. Задания

З а д а н и е 1. Решить дифференциальное уравнение (ДУ) ; у(0) = 1 на отрезке [0, 1] с шагом h = 0,1 методом Эйлера. Для проверки расчетов использовать точное решение .

У к а з а н и я к выполнению задания.

Суть метода Эйлера заключается в вычислении для последовательного набора значений аргумента х приближенных значений искомой функции у = y(x) по формуле у_i+1 = y_i + hf(x_i, y_i); i = 0, 1, 2, 3, … . В данном примере x_i+1 = x_i + 0,1; y₀ = y(0); у_i+1 = y_i + 0,1*2*x_i*y_i; f(x_i, y_i) = 2х_iу_i ; i = 0…10.

В столбце А расположим значения х_i, в В – значения производной, в С – приб- лиженные значения искомой функции, в столбце D – точные ее значения, полученные по аналитической формуле для решения ДУ.

Откройте чистый лист электронной книги и введите (не забывая о возможностях Excel по созданию арифметической прогрессии) в ячейки А1:А11 последовательный ряд чисел от 0 до 1 с шагом 0,1. Это значения х_i, причем при х₀ = 0 значение искомой функции известно (y₀ = y(0) = 1), а при остальных – надо рассчитывать.

В ячейку В1 введите 0, это значение производной (т. е. правой части ДУ) при х = х₀ = 0. В ячейку C1 введите 1, это значение искомой функции в начальной точке х₀.

В ячейки В2 и С2 введите формулы «=2*А1*С1» и «=С1 + 0,1*В2» для вычисления производной и приближенного значения функции при х = х₁. Отметьте, что в ячейках А1 и С1 находятся x₀ и f(x₀, y₀) соответственно. Скопируйте эти две формулы в остальные ячейки диапазона В3:С11.

В ячейку D1 введите формулу «= EXP(A1^2)» для вычисления точного значения искомой функции. Скопируйте эту формулу в ячейки D2:D11.

Р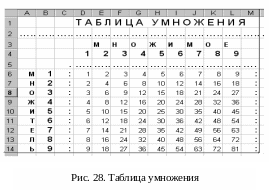 ешение задачи закончено. В ячейках С2:С11 находятся приближенные значения искомой функции, а в D2:D11 – ее точные значения. Теперь по данным диапазона C2:D11 можно построить графики и сравнить кривую Эйлера (приближенное решение) ДУ с его точным решением.

З а д а н и е 2. Составьте таблицу умножения, вводя формулу в ячейку D6 и копируя ее в остальные ячейки диапазона D6:L14 (рис. 28). Не забудьте об автозаполнении и использовании абсолютной и относительной адресации!

З а д а н и е 3. Для функции двух переменных у = sin(x + e^xt), рассмотренной в подразд 9.2, постройте два семейства графиков. Для первого семейства параметром является переменная t (рис. 29), а для второго – х.

З а д а н и е 4. Фирма «Подшипник» выпускает подшипники типов А, В, С. Совет директоров обсуждал изменения, которые нужно внести в план производства в следующем году. Члены совета по каждому из изделий должны высказать мнение – уменьшить выпуск, не менять или увеличить его. Результаты голосования по отдельным типам изделий:

А – «уменьшить выпуск» – 13 %; «не менять» – 20 %; «увеличить выпуск» – 67 %;

В – «уменьшить выпуск» – 28 %; «не менять» – 36 %; «увеличить выпуск» – 36 %;

С – «уменьшить выпуск» – 11 %; «не менять» – 74 %; «увеличить выпуск» – 15 %.

Используя эти данные, составьте электронную таблицу, дайте соответствующие заголовки строкам и столбцам. Постройте следующие диаграммы:

круговую по каждому типу изделия (в отдельности);

столбцовые (гистограммы) для всех типов подшипников по каждому из трех ответов в отдельности (т. е. одна диаграмма –- для ответа «уменьшить выпуск», другая – «не менять», третья – «увеличить выпуск»);

столбцовые для каждого из трех ответов для всех типов подшипников (т. е. первые три столбика соответствуют ответу «уменьшить выпуск», следующие три – «не менять», еще три – «увеличить выпуск»).

Всего должно быть девять диаграмм. Дайте заголовки диаграммам и их отдельным элементам.

З а д а н и е 5. Создайте рабочую книгу «Рейтинг учета текущей успеваемости студентов группы 41-г по информатике в 2001/2002 учебном году». Книга должна состоять из трех рабочих листов с именами «Семестр 1», «Семестр 2» и «Оценки». Первые два листа отличаются незначительно. Они содержат баллы по трем контрольным неделям и средний балл за семестр по каждому студенту, а также общий средний балл за семестр по группе в целом. Баллы выставляются преподавателем каждому студенту в пределах от 0 до 100 в зависимости от его успехов. В таблице должны быть сведения о 15 студентах. Примерный вид таблицы для первого семестра приведен на рис. 30.

Рис. 30. Вид таблицы рабочего листа « Семестр 1»

Все средние баллы первых двух листов, средние баллы за год и предложенные оценки вычисляются в таблицах. Таблица «Семестр 2» получена копированием и редактированием таблицы «Семестр 1».

Все исходные данные для таблицы «Оценки» получены копированием из первых двух таблиц. Все средние баллы на экране округлены до целых значений. Третий лист книги должен иметь вид, изображенный на рис. 31.

Предлагаемая «автоматом» оценка за год по любому предмету по среднему баллу за год выставляется при следующих условиях.

Если средний балл находится в пределах 92 – 100, то выставляется оценка 5 (предлагаемая оценка), если 83 – 91, то выставляется оценка 4, если 65 – 82, то – 3, если не более 64, то – 2;

З а д а н и е 6. Найдите корень уравнения x*|sin(x)| = cos (x/2), принадлежащий отрезку [0; 2] методом Подбора параметра. Для определения начального приближения к корню уравнения протабулируйте с шагом 1 и постройте ее график. Ответ: х  1,022.

З а д а н и е 7. Найдите абсциссы точек пересечения кривых у = sin(x) и y = x²+0,1. Ответ: х₁  0,113; х₂  0,774.

З а д а н и е 8. Найдите абсциссы точек пересечения кривых у = е^х и (х – 1)² + (у – 2)² = 1. Ответ: х₁  0,274; х₂  1,097.

Рис. 31. Вид таблицы рабочего листа «Оценки»

З а д а н и е 9. Найдите минимальное значение функции е^х - 2, если известно, что эта точка принадлежит окружности (х – 1)² + у² = 1. Ответ: х  0,273.

У к а з а н и е. Сначала надо найти точки пересечения кривых, а затем из них выбрать ту точку, у которой ордината меньше.

З а д а н и е 10. Решить задачу линейного программирования:

У к а з а н и е. Целочисленность задается, как и другие ограничения, в поле Ограничения диалогового окна Поиск решения.

З а д а н и е 11. Записать макрос Подписи (сочетание клавиш – Ctrl + п), который позволяет в любое место ЭТ вставить табличку, изображенную на рис. 32.

Фирма "Подшипник"
Директор	Сидоров А. А.
Главный инженер	Козлов С. И.
Инженер по ТБ	Васильев П. Р.

Рис. 32. Результат работы макроса Подписи

З а д а н и е 12. Выполните индивидуальное задание по созданию таблицы Excel, выданное преподавателем. Представьте преподавателю (на экране) отчет в виде разработанной таблицы Excel.

Лабораторная работа 10

ОФОРМЛЕНИЕ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

Для профессионального выполнения и оформления расчетно-графических работ, необходимо рассмотреть некоторые дополнительные сведения: панель Рисования и способы обмена данными между различными приложениями MS Office, а также между ними и другими пакетами.