2.2. Примеры решения задач

Пример 1. Определить число N молекул, содержащихся в объеме V = 1 мм³ воды, массу молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.

Решение: Число N молекул, содержащихся в некоторой массе равно произведению числа Авогадро на количество вещества :

так как количество вещества:

μ - молярная масса, то

Выразив в этой формуле массу, как произведение плотности на объем V, получим

. (1)

Подставим в формулу (1) следующие значения величин: = 10³ кг/м³,

V = 1 мм³ = м , μ = кг/моль, = моль и произведем вычисления:

молекул = 3,34 10¹⁹молекул.

Массу , одной молекулы можно найти делением молярной массы на число Авогадро:

Подставим сюда числовые значения μ и и найдем массу молекулы воды:

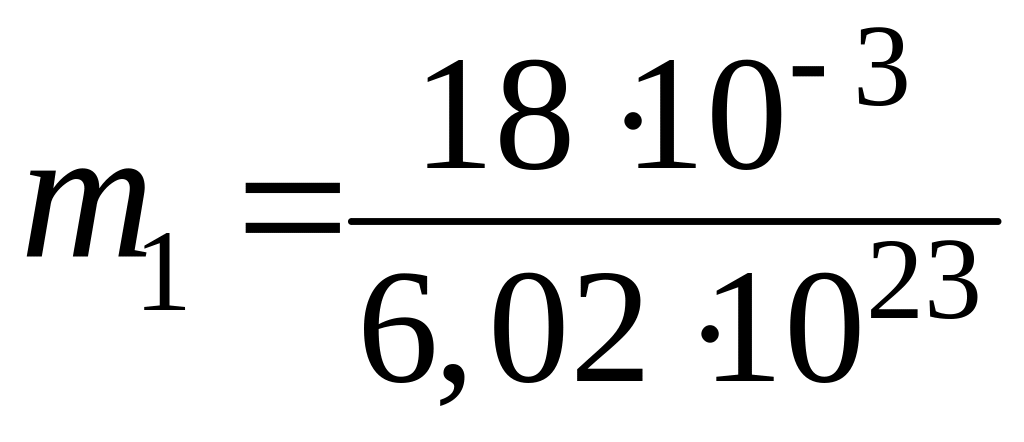кг = кг.

Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) , где d - диаметр молекулы воды. Отсюда

(2)

Объем найдем, разделив молярный объем на число молекул в моле, т.е. на число Авогадро :

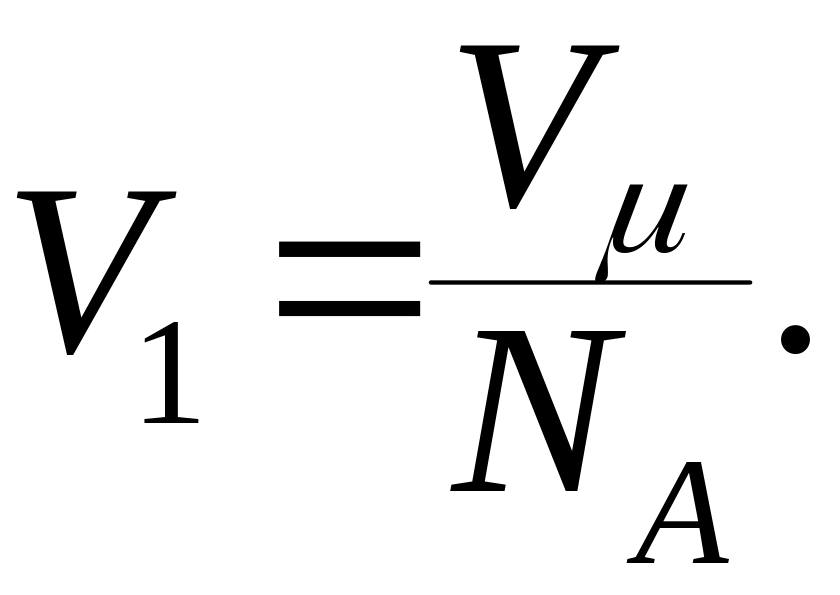
Подставим полученное выражение в формулу (2):

Входящий в эту формулу молярный объем определяется выражением , тогда искомый диаметр молекулы:

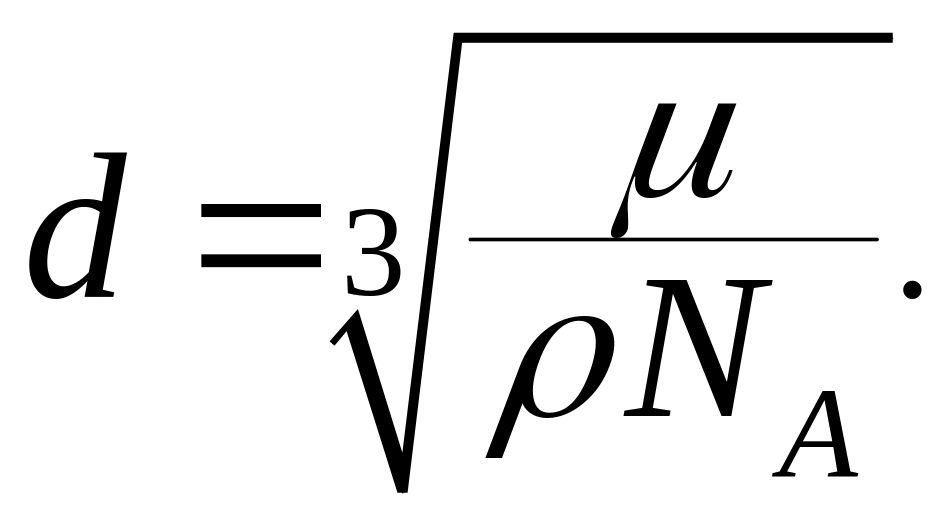(3)

Проверим, дает ли правая часть выражения (3) единицу длины:

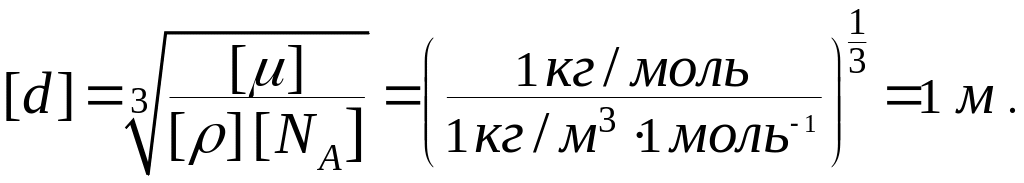
Теперь подставим числовые значения физических величин в формулу (3) и произведем вычисления:

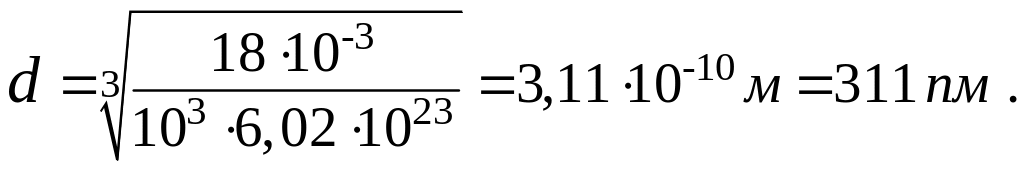
Пример 2. В баллоне объемом V = 10 л находится гелий под давлением Р = 1 МПа и при температуре Т = 300 К. После того, как из баллона было взято m = 10 г гелия, температура в баллоне понизилась до Т = 290 К. Определить давление Р гелия, оставшегося в баллоне.

Решение: Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа:

(1)

где - масса гелия в баллоне в конечном состоянии, μ - молярная масса гелия, R - универсальная газовая постоянная. Из уравнения (1) выразим искомое давление Р .

(2)

Массу гелия m₂ выразим через массу m₁, соответствующую начальному состоянию и массу m гелия, взятого из баллона:

(3)

Массу гелия m найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию

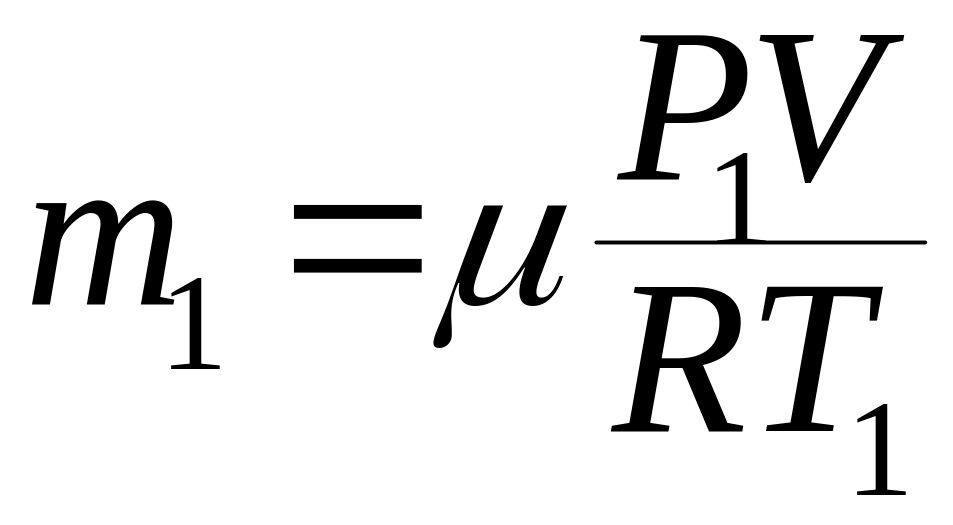(4)

Подставляя в выражение (3) массу из формулы (4), а затем полученное выражение в формулу (2), найдем:

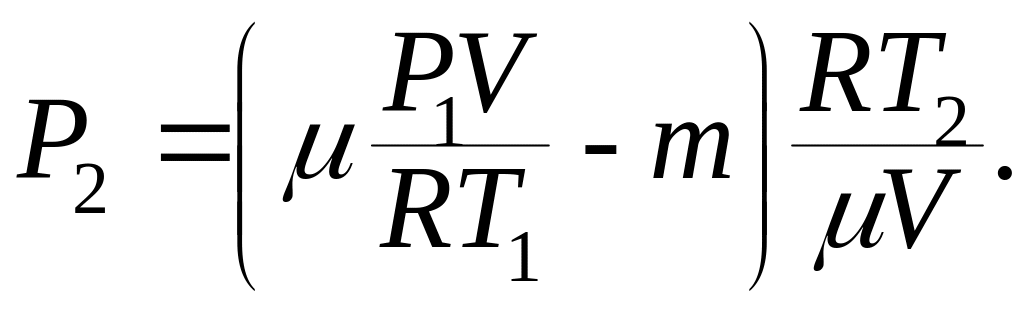
После преобразования и сокращения находим:

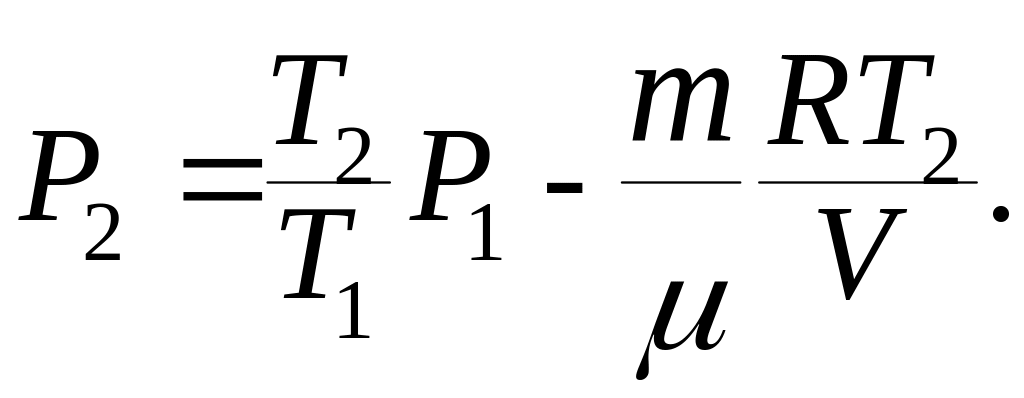(5)

Левая часть расчётной формулы (5) выражает давление, имеет размерность . Проверим размерность правой части. Размерность первого слагаемого не вызывает сомнения, т.к. отношение температур – величина безразмерная. Размерность второго слагаемого:

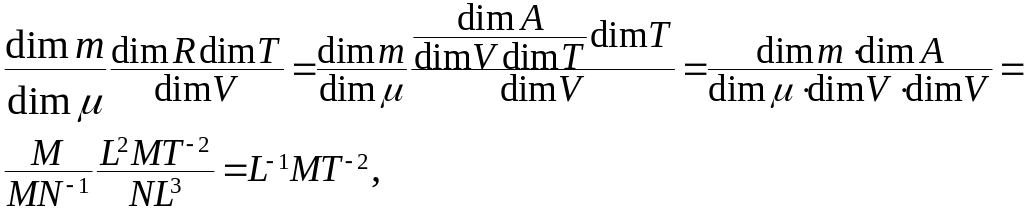
что совпадает с размерностью давления.

Убедившись в том, что размерность правой и левой частей формулы (5) одинаковы, выразим величины, входящие в эту формулу, в единицах СИ и произведем вычисления:

P₁ = 1 МПа =10⁶ Па, , ,

R = 8,31 Дж/(мольК), T₁ = 300 К, T₂ = 290 К,

V = 10 л = 10^-2 м³,

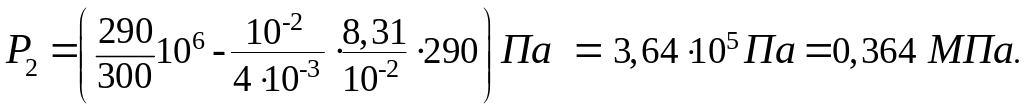
Пример 3. Баллон содержит = 80 г кислорода и = 320 г аргона. Давление смеси Р = 1 МПа, температура Т = 300 К. Принимая данные газа за идеальные, определить объем V баллона.

Решение. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. Парциальным давлением газа называется давление, которое производил бы этот газ, если бы только он один находился в сосуде, занятым смесью. По уравнению Менделеева-Клапейрона, парциальные давления кислорода и аргона выражается формулами:

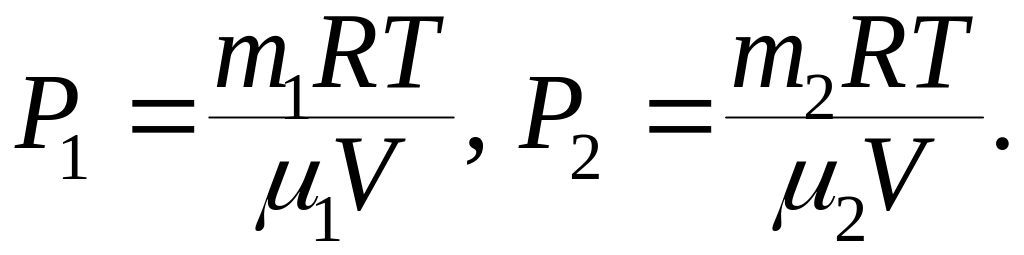
Следовательно, по закону Дальтона давление смеси газов

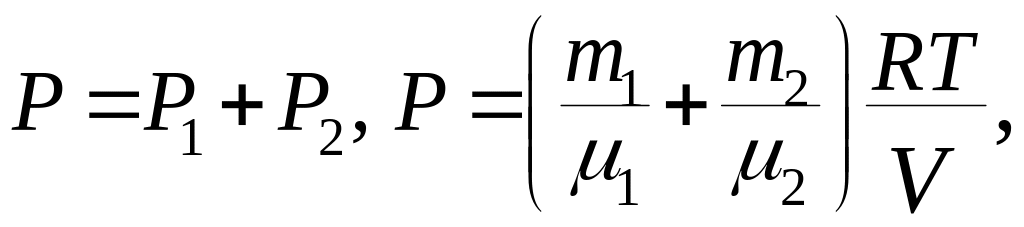
откуда объем баллона:

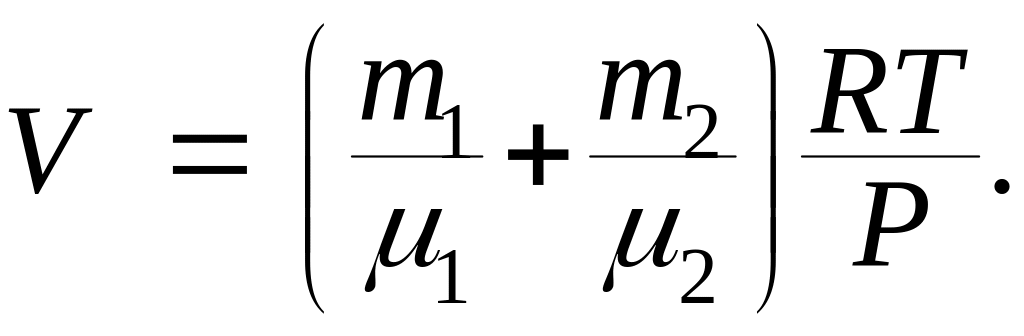
Выразим в единицах СИ числовые значения величин, входящих в эту формулу m₁ = 80 г = 0,8 кг, , m₂ = 330 г = 0,33 кг, , ₂ = 40 10^-3 кг/моль, P₁ = 1 МПа = 10⁶ Па, R = 8,31 Дж/(мольК), подставим числовые значения в формулу и произведем вычисления:

Пример 4. Найти среднюю кинетическую энергию вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию вращательного движения всех молекул кислорода массой m = 4 г.

Решение: Известно, что на каждую степень свободы молекулы газа приходится одинаковая средняя энергия , где - постоянная Больцмана, Т - абсолютная температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода двухатомная) соответствует две степени свободы, то средняя энергия вращательного движения молекулы кислорода выразится формулой:

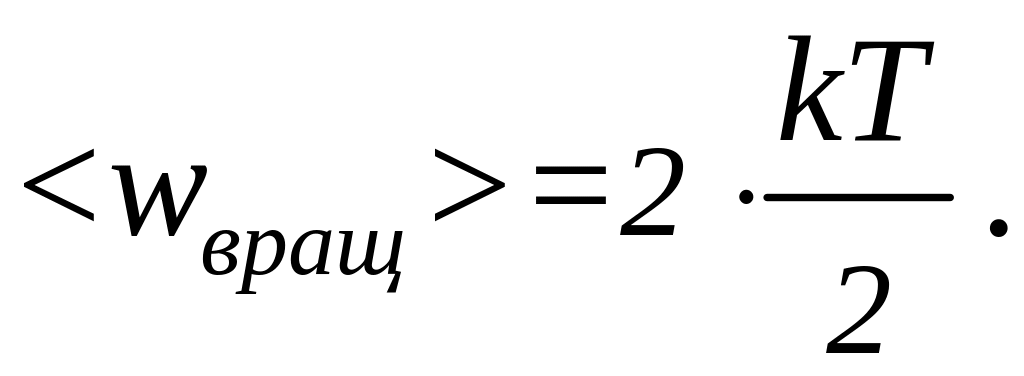(1)

Подставив в формулу (1) значение и T = 350 К получим . Кинетическая энергия вращательного движения всех молекул газа определяется равенством:

(2)

Число всех молекул газа можно вычислить по формуле:

(3)

где число Авогадро, - количество вещества. Если учесть, что количество вещества 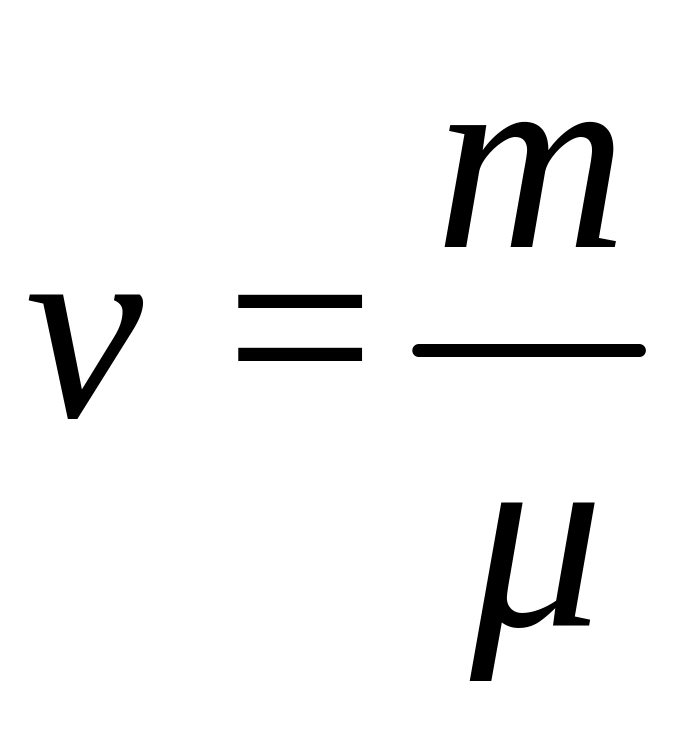, где - масса газа, μ - молярная масса газа, то формула (3) примет вид:

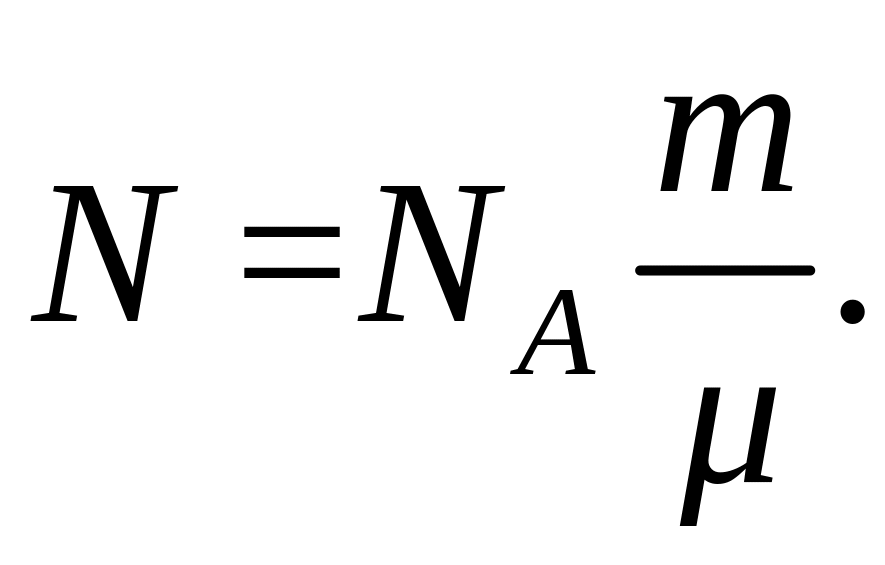
Подставив это выражение в формулу (2) получим:

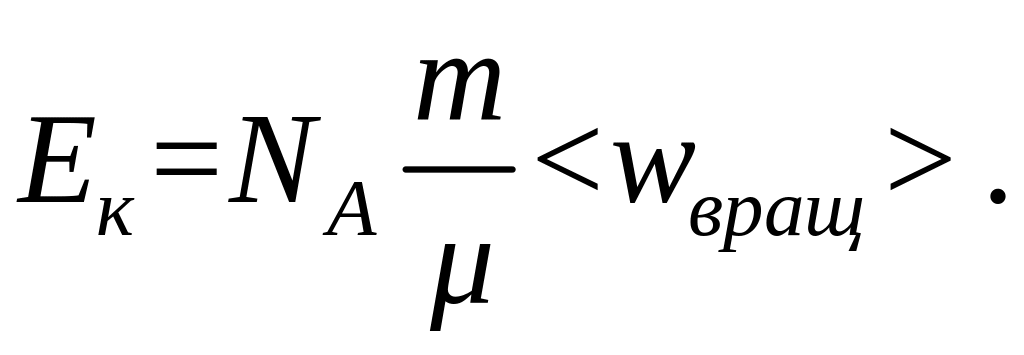(4)

Выразим величины, входящие в эту формулу, в единицах СИ:

, , , . Подставив эти значения в формулу (4), найдем: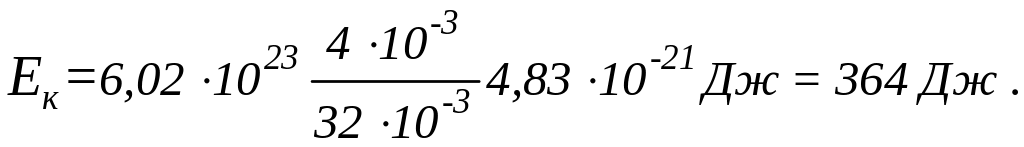

Пример 5. Вычислить удельные теплоемкости при постоянном объеме и при постоянном давлении неона и водорода, принимая эти газы за идеальные.

Решение: Удельные теплоемкости идеальных газов выражаются формулами

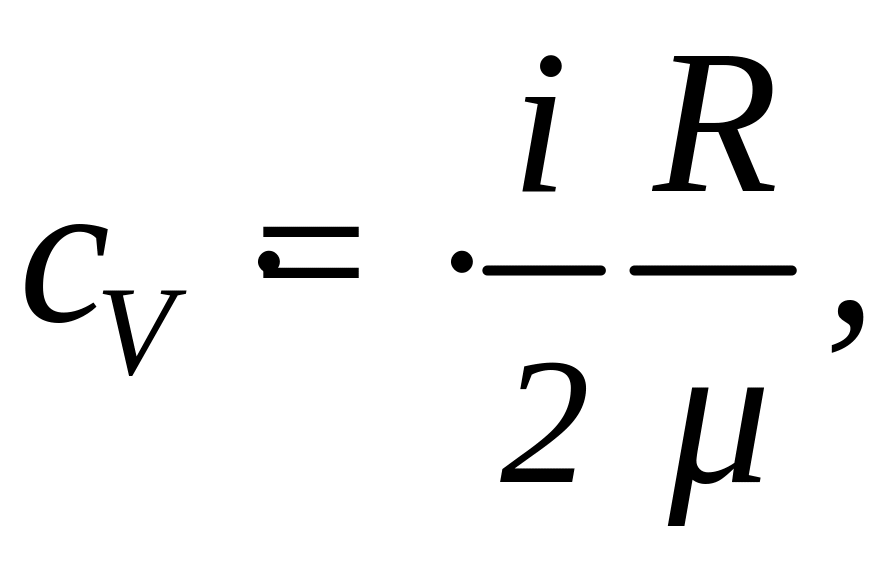(1)

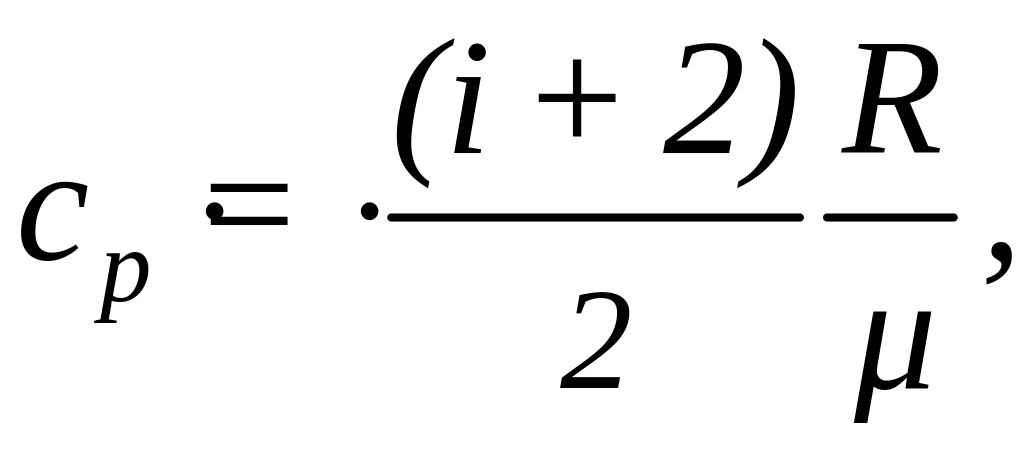(2)

где - число степеней свободы молекул газа, - молярная масса. Для неона (одноатомный газ) , кг/моль (см. справочную таблицу). Вычисляя по формулам (1) и (2), получим:

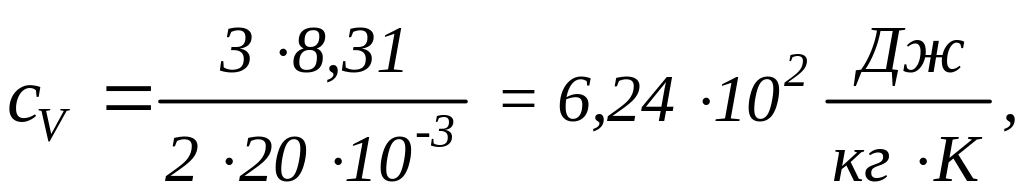
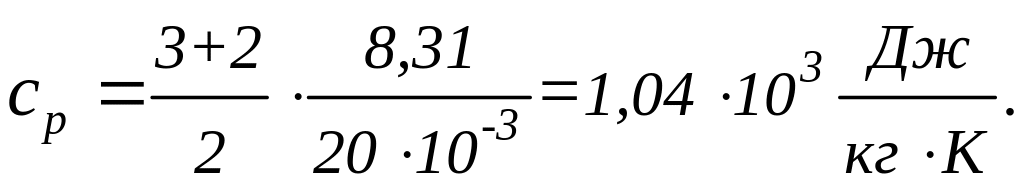
Для водорода (двухатомный газ) , кг/моль. Вычисляя по тем же формулам, получим:

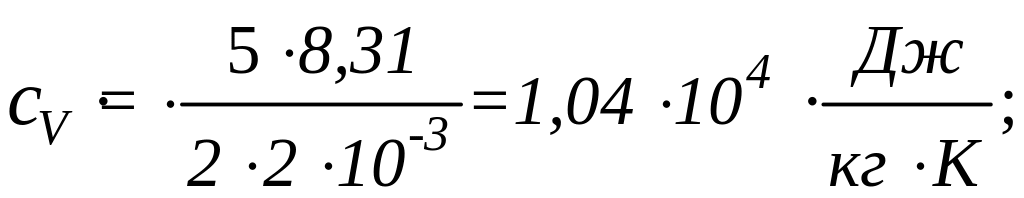
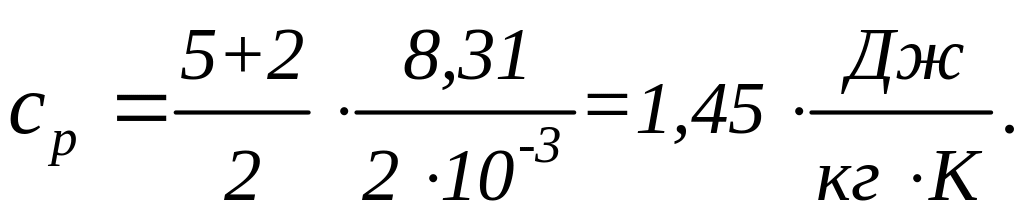
Пример 6. Вычислить удельные теплоемкости и смеси неона и водорода, если массовая доля неона = 80%, массовая доля водорода = 20%. Значение удельных теплоемкостей газов взять из предыдущего примера.

Решение: Удельную теплоемкость смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на , выразим двумя способами.

(1)

(2)

где - удельная теплоемкость неона, - удельная теплоемкость водорода. Приравняв правые части (1) и (2) и разделив обе части полученного равенства на . получим:

отсюда

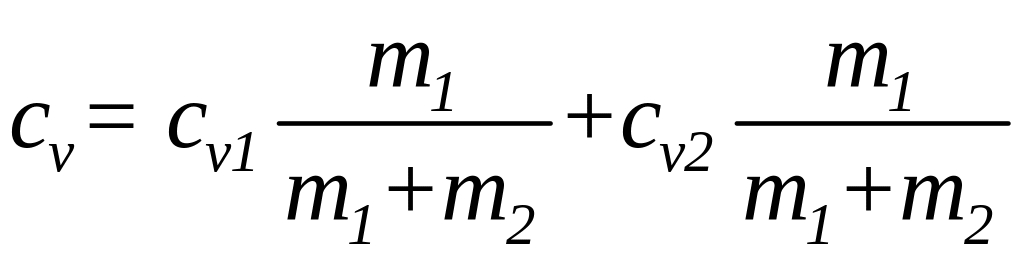(3)

или

(4)

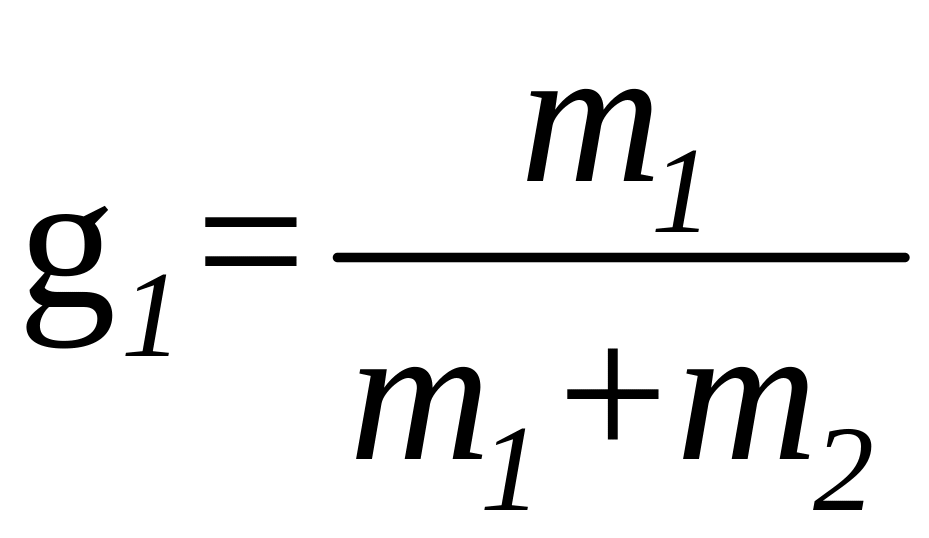где и 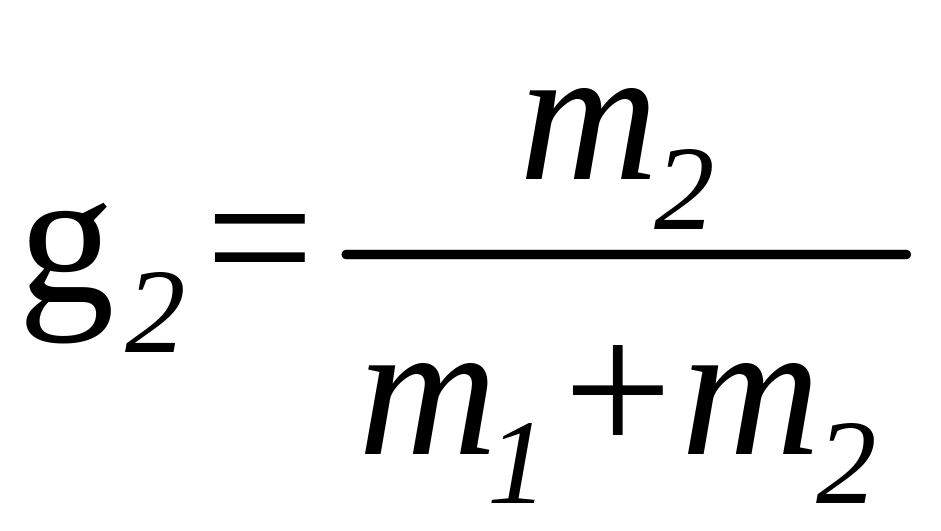- массовые доли неона и водорода в смеси. Подставив в формулу (4) числовые значения величин, найдем:

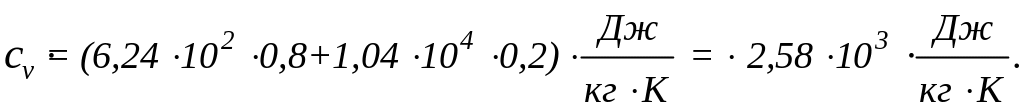
Рассуждая таким же образом, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

(5)

Подставим в формулу (5) числовые значения величин:

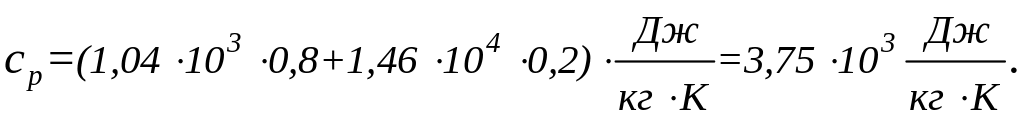
Пример 7. Кислород массой m = 2 кг занимает объем равный V = 1 м³ и находится под давлением P = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂= 3 м³, а затем при постоянном объеме до давления Р = 0,5 МПа. Найти изменение внутренней энергии газа, совершенную им работу А и теплоту Q , переданную газу. Построить график процесса.

Решение: Изменение внутренней энергии газа выражается формулой:

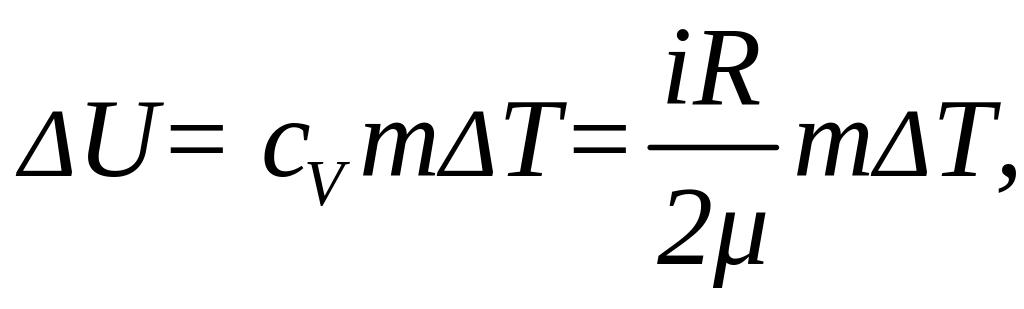(1)

где i - число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5), μ - молярная масса. Начальную и конечную температуру газа найдем из уравнения Клапейрона-Менделеева:

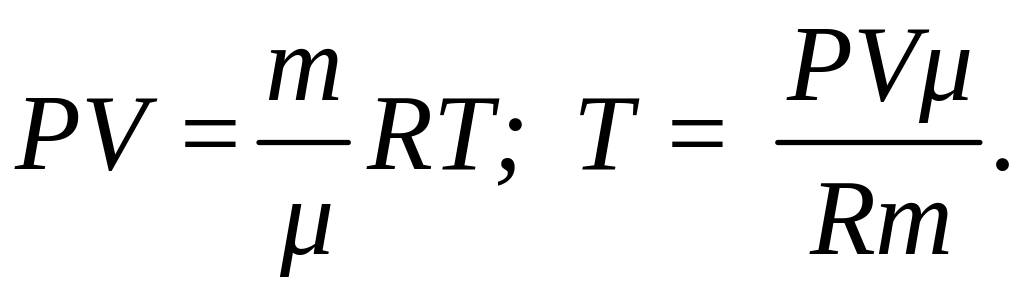(2)

Выпишем заданные величины в единицах системы СИ: , кг/моль, = 8,31 Дж/моль К, V = 1 м , V₂ = V₃ = 3 м ³, P = P₂ = 0,2 МПа = 2 10⁵ Па, Р = 0,5 МПа = 5 10⁵ Па. Подставляя эти значения в выражение (2) и выполняя арифметические действия, получим:

;

; .

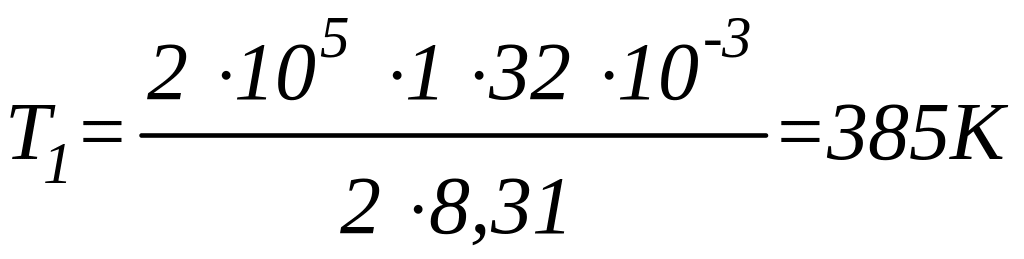Подставляя в выражение (1) числовые значения величин, входящих в него и выполняя арифметические действия, находим:

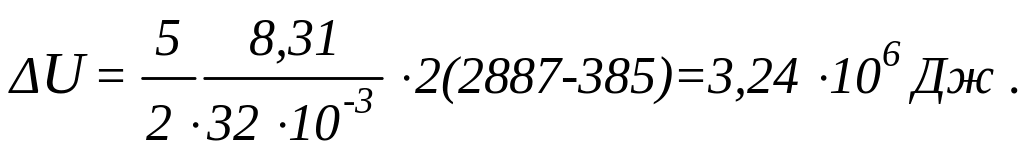
Работа расширения газа при постоянном давлении выражается формулой:

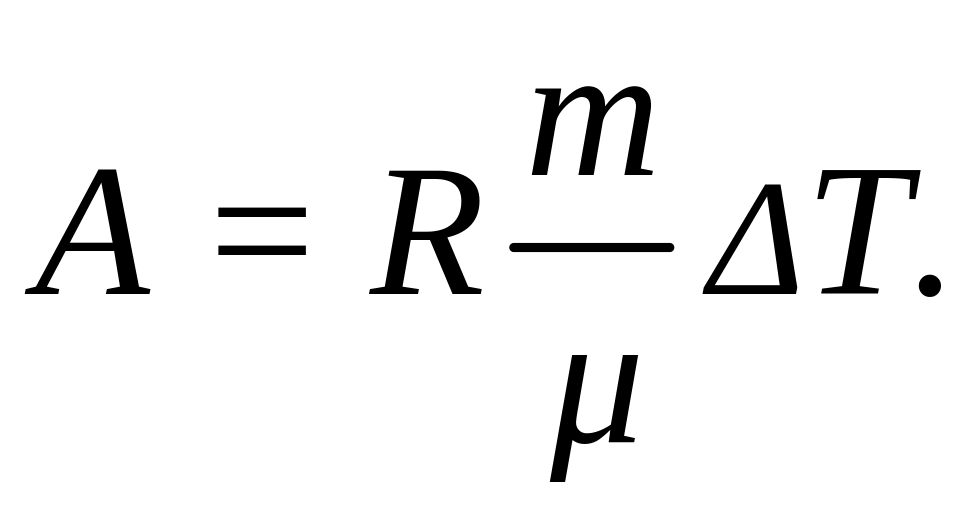
Подставим числовые значения величин, получим:

.

Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. . Следовательно, полная работа, совершенная газом, равна

= Дж.

Согласно первому началу термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии и работы A: , следовательно .

Пример 8. Тепловая машина работает по обратному циклу Карно. Температура нагревателя T = 500 К. Определить термический КПД цикла и температуру Т₂ охладителя тепловой машины, если за счет каждого килоджоуля теплоты, полученной от нагревателя, машина совершает работу А = 350 Дж.

Решение: Термический КПД тепловой машины, называемый также коэффициентом использованной теплоты, показывает, какая доля теплоты, полученной от нагревателя, превращается в механическую работу. Термический КПД выражается формулой:

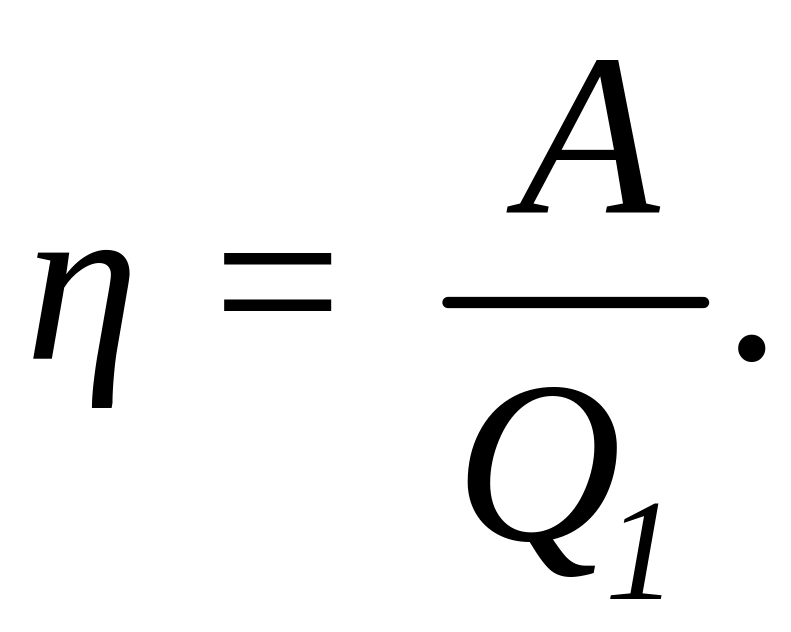
где Q - теплота, полученная от нагревателя, А - работа, совершаемая рабочим телом тепловой машины. Подставив числовые значения в эту формулу, получим

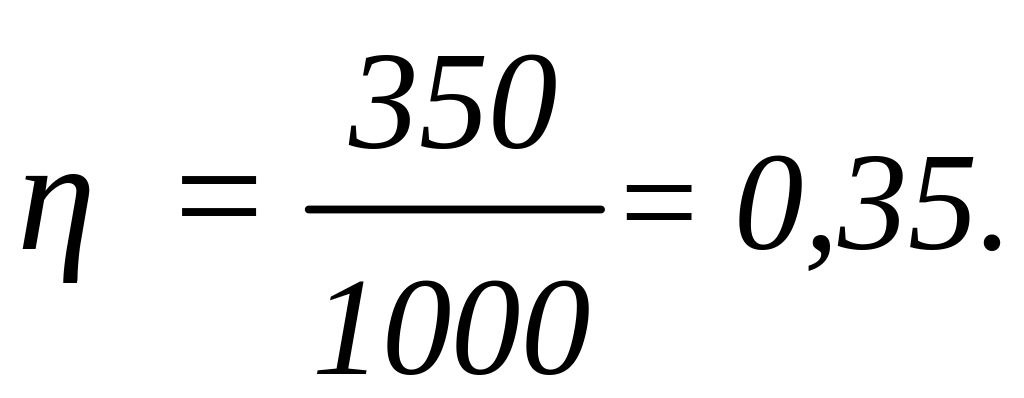
Зная КПД цикла, можно по формуле 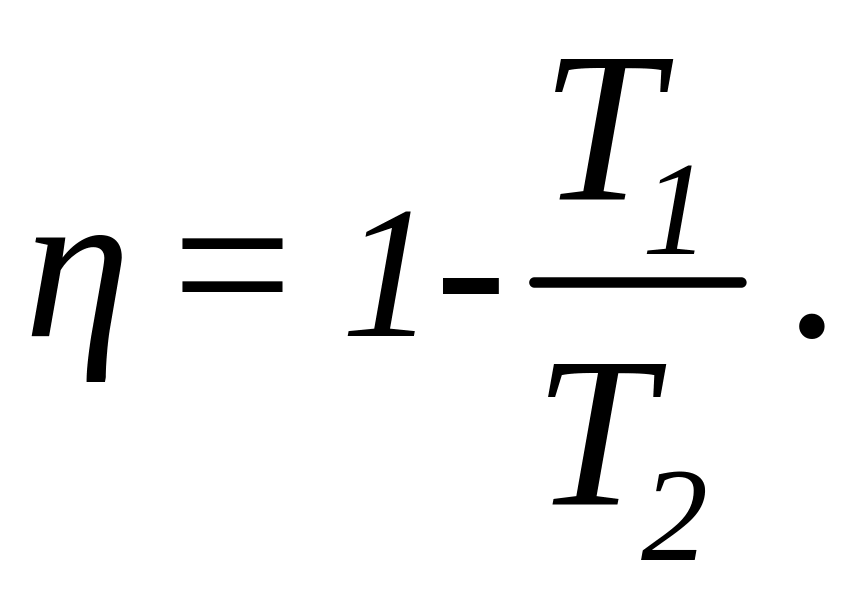определить температуру охладителя Т₂:

Подставив в эту формулу полученное значение КПД и температуры T нагревателя, получим:

Пример 9. Найти добавочное давление внутри мыльного пузыря диаметром d = 10 см. Какую работу нужно совершить, чтобы выдуть этот пузырь?

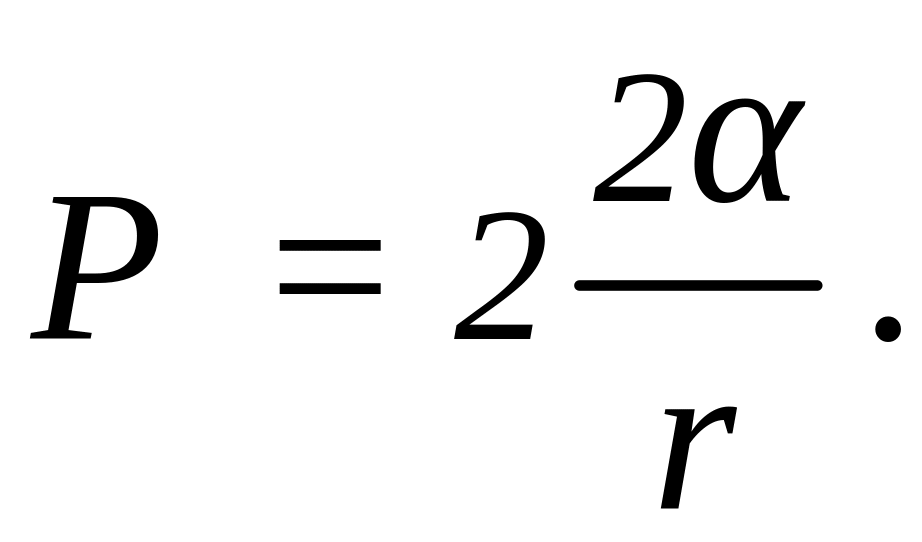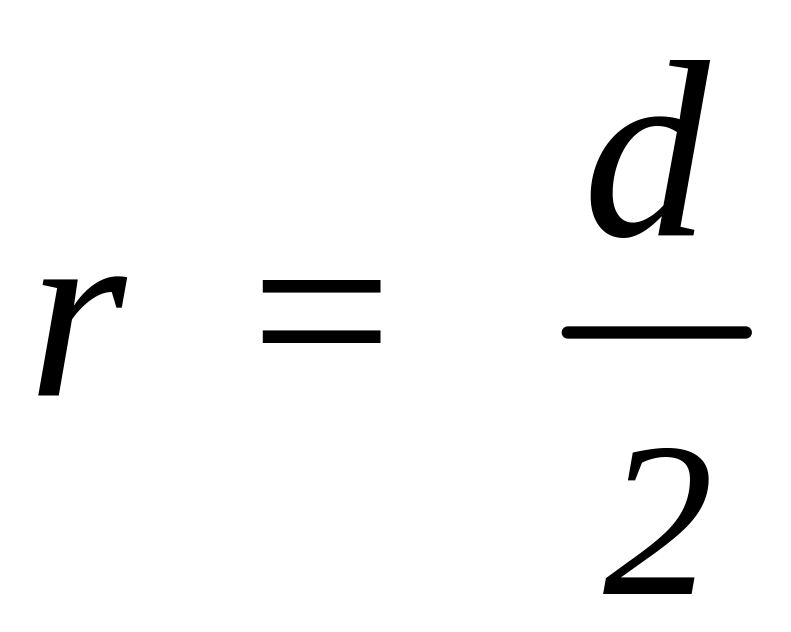Решение: Пленка мыльного пузыря имеет две сферические поверхности - внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление, где - . где радиус пузыря. Так как , то 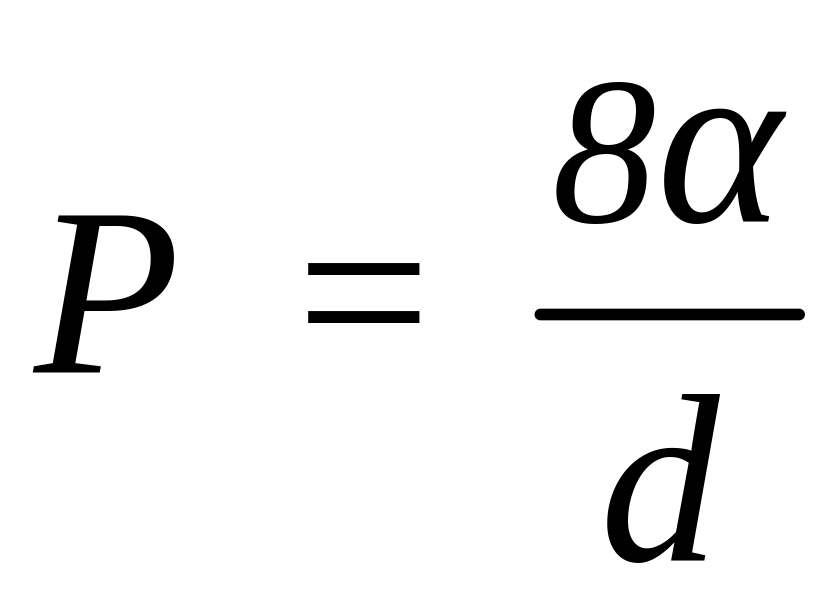. Коэффициент поверхностного натяжения мыльной воды 40 мН/м (см. справочную табл.) диаметр пузыря = 10 см = 0,1 м.

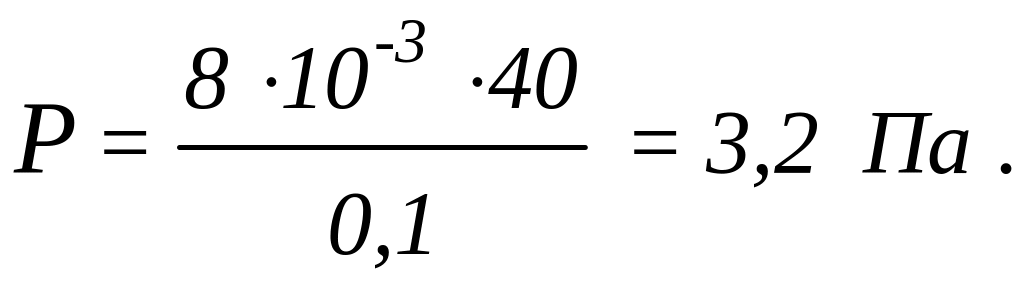
Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить её поверхность на , выражается формулой

В данном случае - общая площадь двух сферических поверхностей пленки, затягивающей отверстие трубки до выдувания пузыря, пренебрегая , получим

Подставив числовые значения величин, получим:

.