
- •З.Н. Есина практикум по физике Учебное пособие Кемерово 2010
- •Предисловие
- •Раздел I.Физические основы механики
- •1.1. Основные формулы
- •19. Связь разности фаз колебаний с расстоянием между точками среды , отсчитанными в направлении распространения колебаний ,
- •1.2. Примеры решения задач
- •1.3. Задачи для самостоятельного решения
- •Раздел II.Молекулярная физика. Термодинамика
- •2.1. Основные формулы
- •2.2. Примеры решения задач
- •2.3. Задачи для самостоятельного решения
- •Раздел III.Электростатика. Постоянный ток
- •3.1. Основные формулы (в единицах си)
- •3.2. Примеры решения задач
- •З.З. Задачи для самостоятельного решения
- •Раздел IV.Электромагнитизм
- •4.1. Основные формулы
- •4.2. Примеры решения задач
- •4.3. Задачи для самостоятельного решения
- •Раздел V.Оптика
- •5.1. Уравнения и формулы
- •5.2. Примеры решения задач
- •5.3. Задачи для самостоятельного решения
- •Литература
- •Справочные таблицы
- •1. Основные физические постоянные
- •2. Диэлектрическая проницаемость
- •3. Удельное сопротивление проводников
- •4. Плотность твёрдых тел
- •5. Плотность жидкостей
- •11. Массы атомов лёгких изотопов
- •12. Масса и энергия покоя некоторых частиц
- •13. Единицы си, имеющие специальные наименования
- •14. Множители и приставки для образования десятичных кратных и дольных единиц и их наименования
Раздел IV.Электромагнитизм
4.1. Основные формулы
1.
Связь магнитной индукции
![]() с напряженностью
с напряженностью
![]() магнитного поля:
магнитного поля:
![]() ,
,
где - магнитная проницаемость изотропной среды;
![]() -
магнитная
постоянная (
-
магнитная
постоянная (![]() ).
В вакууме
).
В вакууме
![]() и тогда магнитная индукция:
и тогда магнитная индукция:
![]() .
.
2. Закон Био - Савара - Лапласа:
![]() ,
или
,
или
![]() ,
,
где
![]() - магнитная индукция поля, создаваемого
элементом проводника длиной
- магнитная индукция поля, создаваемого
элементом проводника длиной
![]() с током
,
с током
,![]() - радиус-вектор,
направленный от элемента проводника
к точке, в которой вычисляется магнитная
индукция;
- радиус-вектор,
направленный от элемента проводника
к точке, в которой вычисляется магнитная
индукция;
![]() -
угол
между радиусом - вектором и направлением
тока в элементе проводника.
-
угол
между радиусом - вектором и направлением
тока в элементе проводника.
3. Магнитная индукция в центре кругового тока:
![]() ,
,
где - радиус кругового витка.
4. Магнитная индукция на оси кругового тока:
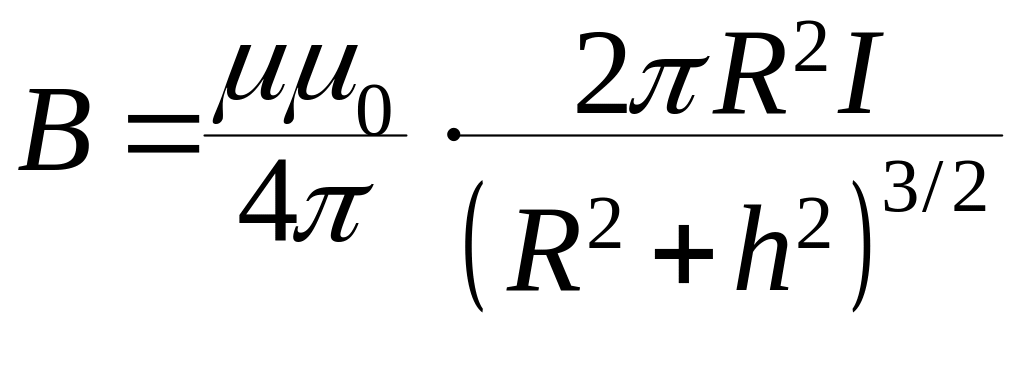 ,
,
где - расстояние от центра витка до точки, в которой вычисляется магнитная индукция.
5. Магнитная индукция поля прямого тока:
![]() ,
,
где - расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
6. Магнитная индукция поля, создаваемого отрезком провода с током (рис. 1. а):
![]() ,
,
О
a)
б)
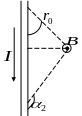
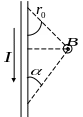
Рис. 1.
При
симметричном расположении провода
относительно точки, в которой определяется
магнитная индукция (рис. 1.б)
![]() =
=
![]() = =
= =![]() ,
тогда
,
тогда
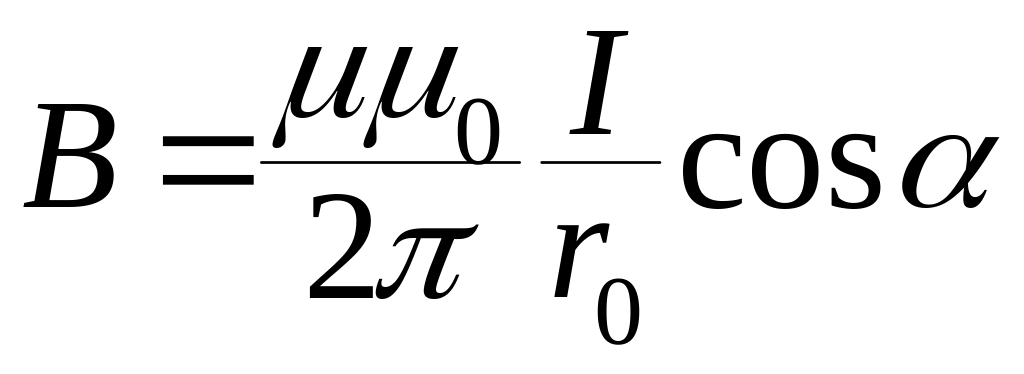 .
.
7. Магнитная индукция поля соленоида:
![]() ,
,
где
![]() -
число
витков соленоида, приходящееся на
единицу длины.
-
число
витков соленоида, приходящееся на
единицу длины.
8. Сила, действующая на проводник с током в магнитном поле, закон Ампера:
![]() ,
или
,
или
![]() ,
,
где - длина проводника; - угол между направлением тока в проводнике и вектором магнитной индукции . Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямолинейным, то закон Ампера можно применять к каждому элементу проводника в отдельности:
![]() .
.
9. Сила взаимодействия параллельных проводников с током:
![]() ,
,
где
![]() - расстояние между проводами.
- расстояние между проводами.
10. Магнитный момент вектора с током:
![]() ,
,
где
- сила тока, протекающего по контуру,
![]() -
площадь
контура, вектор
-
площадь
контура, вектор
![]() численно равен площади
контура и совпадает по направлению с
вектором нормали к плоскости контура.
численно равен площади
контура и совпадает по направлению с
вектором нормали к плоскости контура.
11. Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:
![]() ,
или
,
или
![]() ,
,
где
- угол
между векторами
![]() и
.
и
.
12. Потенциальная энергия контура с током в магнитном поле:
![]() ,
или
,
или
![]() .
.
За
нулевое значение потенциальной энергии
контура с током в магнитном поле принято
расположение контура, когда вектор
![]() перпендикулярен вектору
.
перпендикулярен вектору
.
13.
Отношение магнитного момента
к
механическому
![]() (моменту
импульса) заряженной частицы, движущейся
по круговой орбите:
(моменту
импульса) заряженной частицы, движущейся
по круговой орбите:
![]() ,
,
где q - заряд частицы, - масса частицы.
14.
Если частица находится одновременно
в электрическом и магнитном полях, то
под силой Лоренца понимают выражение
![]() :
:
![]() или
или
![]() ,
,
где
![]() - скорость
заряженной частицы,
- угол
между векторами
- скорость
заряженной частицы,
- угол
между векторами
![]() и
.
и
.
15. Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
![]() или
или
![]() ,
,
где - площадь контура; - угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности
![]() ,
,
интегрирование ведется по всей поверхности.
16. Потокосцепление (полный поток):
![]() ,
,
Эта
формула применима для соленоида и
тороида с равномерной намоткой плотно
прилегающих друг к другу
![]() витков.
витков.
17. Работа по перемещению замкнутого контура в магнитном поле:
![]() .
.
18. Э.Д.С. индукции:
![]() .
.
19.
Разность потенциалов на концах
проводника, движущегося со скоростью
![]() в
магнитном поле:
в
магнитном поле:
![]() ,
,
где - длина проводника; - угол между векторами и .
20. Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:
![]() ,
или
,
или
![]() ,
,
где - сопротивление контура.
21. Индуктивность контура:
![]() .
.
22. Э.Д.С. самоиндукции:
![]() .
.
23. Индуктивность соленоида:
![]() ,
,
где
-
число витков, приходящееся на единицу
длины соленоида;
![]() - объём
соленоида.
- объём
соленоида.
24. Мгновенное значение силы тока в цепи, обладающей сопротивлением и индуктивностью :
а) при замыкании цепи:
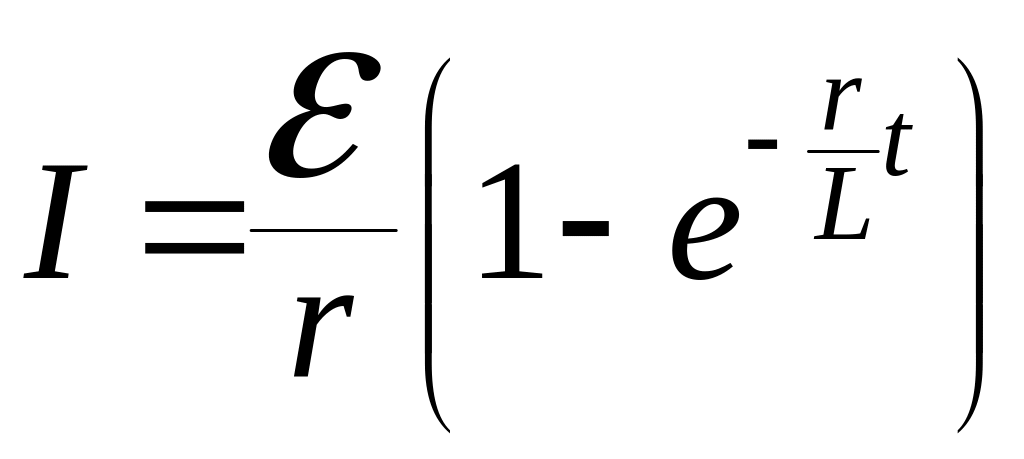 ,
,
где
![]() - Э.Д.С. источника тока;
- время, прошедшее после замыкания цепи;
- Э.Д.С. источника тока;
- время, прошедшее после замыкания цепи;
б) при размыкании цепи:
![]() ,
,
где
![]() - значение силы тока цепи при
- значение силы тока цепи при
![]() = 0;
-
время,
прошедшее с момента размыкания цепи.
= 0;
-
время,
прошедшее с момента размыкания цепи.
25. Энергия магнитного поля:
![]() .
.
26. Объёмная плотность энергии магнитного поля (энергия, заключенная в единице объёма):
![]() ,
или
,
или
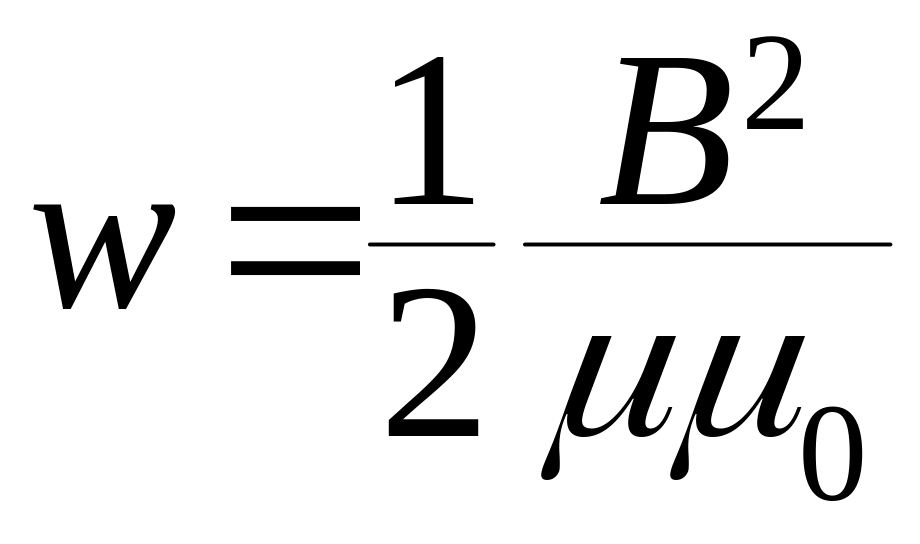 ;
или
;
или
![]() ,
,
где
![]() - магнитная
индукция;
- магнитная
индукция;
![]() - напряженность
магнитного поля.
- напряженность
магнитного поля.
