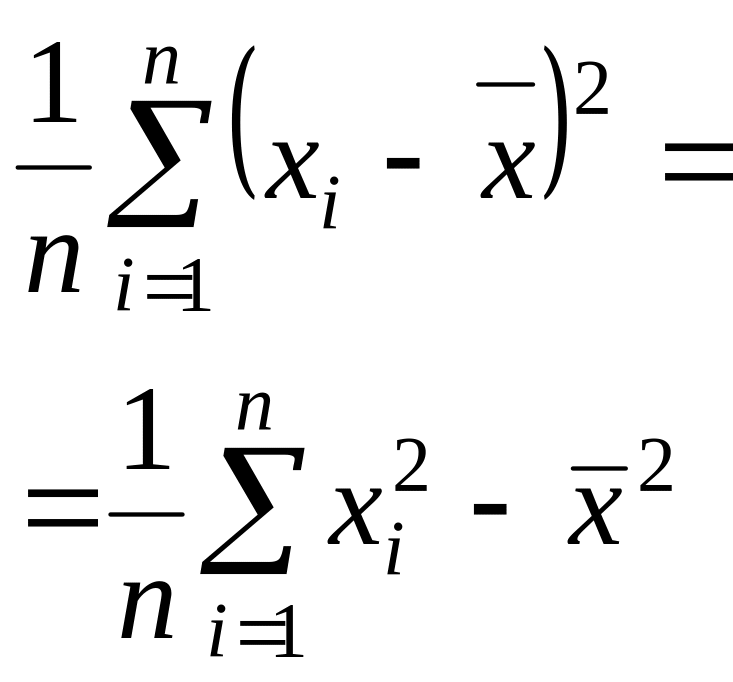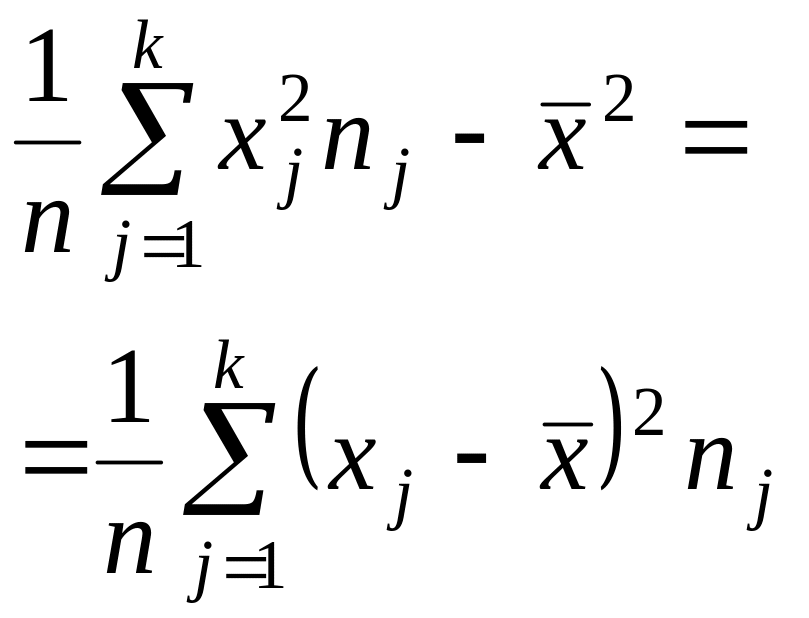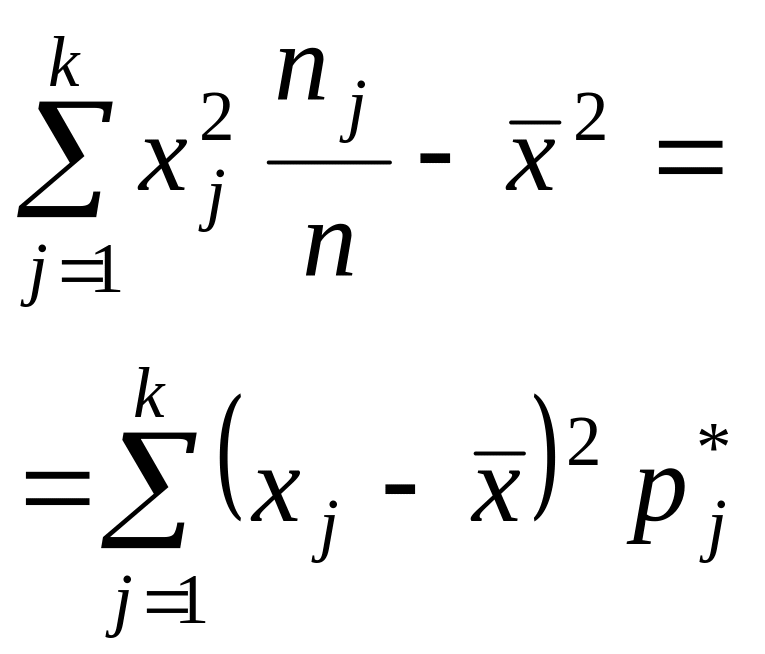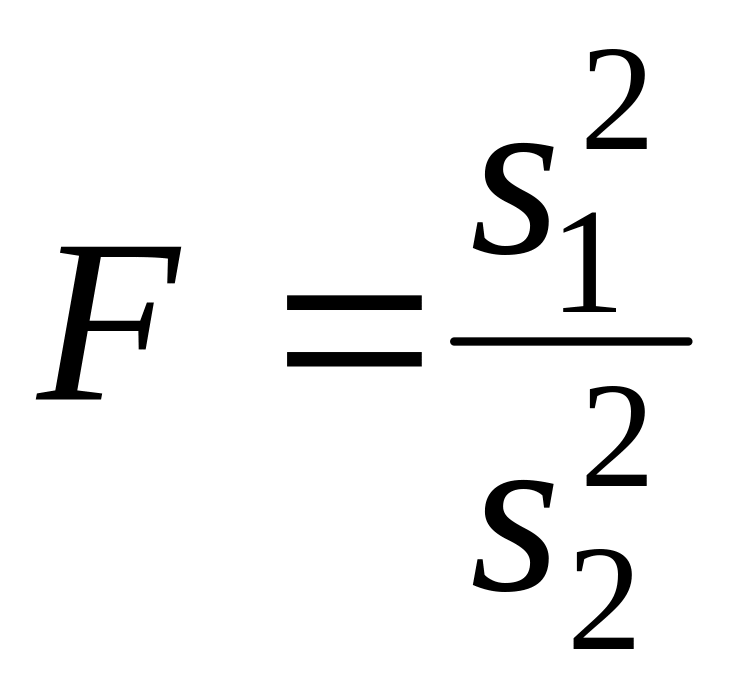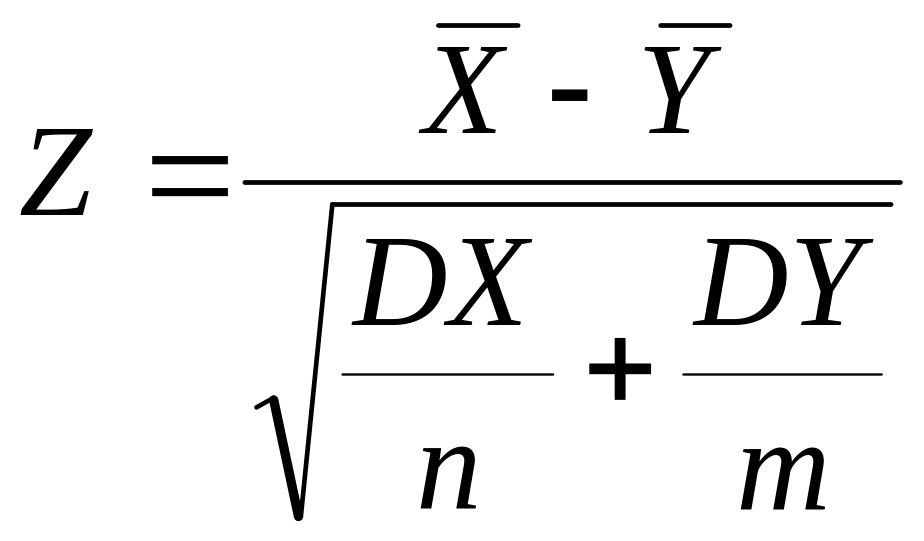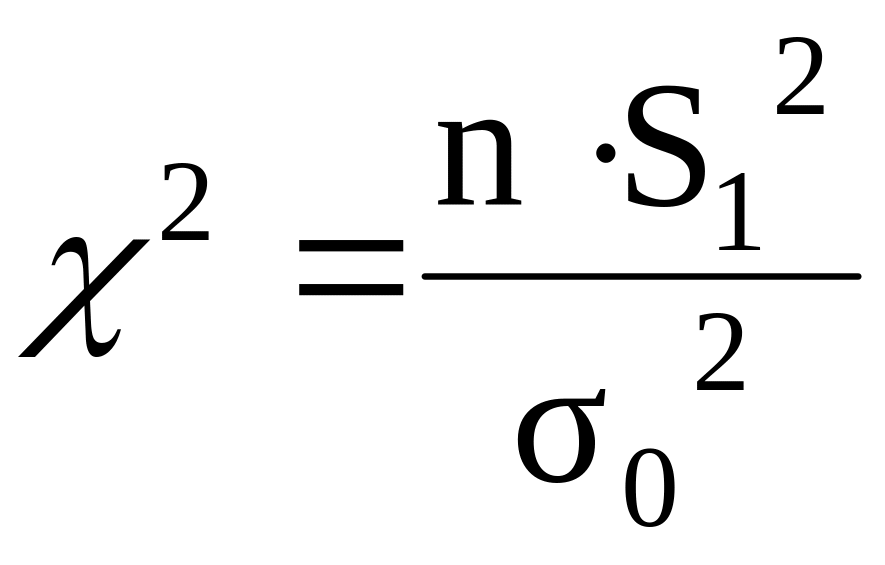- •Приложение 3 Алгоритмы решения ключевых задач
- •II. Комплексные умения и алгоритмы к разделу 2 «Дискретные и непрерывные случайные величины»
- •III. Комплексные умения и алгоритмы к разделу 3 «Элементы математической статистики»
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Вычисление вероятности событий по определению Задача № 2-а. Студент знает ответы на 18 вопросов зачета из 30. Какова вероятность того, что он вытащит на зачете известный ему вопрос? Решение:
- •Вычисление вероятностей событий с помощью соединений
- •Вычисление вероятности события a по формуле полной вероятности. Вычисление вероятности одной из гипотез по формуле Байеса. Задача № 5.
- •Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Бернулли
- •Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Пуассона
- •Алгоритм № 8
- •Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли.
- •Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании
- •Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов гипергеометрических распределений
- •Вычисление числовых характеристик нсв,
- •Вычисление числовых характеристик нсв, равномерно распределенной на отрезке [a,b], а также вероятность
- •Вычисление числовых характеристик нсв, имеющей показательное распределение на отрезке [a,b]
- •III. Комплексные умения и алгоритмы к
- •Разделу 3 «Элементы математической статистики»
- •Алгоритм на умение №18
- •Построение вариационного ряда, эмпирической функции распределения и ее графика - кумуляты.
- •Алгоритм на умение №2/19 Построение полигона и гистограммы
- •Алгоритм на умение №4/21 Вычисление точечной несмещенной оценки для дисперсии
- •Алгоритм на умение № 5/22
- •Алгоритм на умение №6/23
- •Вычисление доверительных интервалов для математического
- •Ожидания m нормального распределения
- •Задача 23.
- •Алгоритм на умение №7/24
- •Вычисление доверительных интервалов для генеральной
- •Дисперсии d и среднеквадратичного отклонения
- •Задача 24.
- •Алгоритм на умение №8/25 Вычисление доверительного интервала для вероятности р наступления события а с помощью таблиц нормального распределения
Алгоритм на умение №8/25 Вычисление доверительного интервала для вероятности р наступления события а с помощью таблиц нормального распределения
Задача 24. Выборочная проверка показала, что из 100 выпускников 87 человек удовлетворяют требованиям стандарта по математике. Мы хотим быть уверены на 95%, что не ошибаемся в оценке процента учащихся, не усвоивших программу. В каких пределах он находится? Каков должен быть объем выборки, чтобы оценить процент брака с точностью до 0.1?
Решение
№ п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму |
1. |
Вычислить
оценку
|
Имеем: n =100, m = 100-87=13, =0.13 |
2. |
Найти доверительный интервал для p, используя формулу для повторной выборки с возвратом. |
|
3. |
Для проверки гипотезы, сформулировать вывод из эксперимента, провести вычисления с доверительным интервалом. |
Неравенство
Т.о., необходимо проверить знания у 44 выпускников. |
Приложение 3
Таблица 1
|
Вариационный ряд задан последовательностью |
Вариационный ряд задан таблицей абсолютных частот |
Вариационный ряд задан таблицей относительных частот |
Среднее
значение выборки |
|
|
|
Дисперсия выборки DВ |
|
|
|
Таблица 2
Моменты |
Вариационный ряд, заданный последовательностью |
Вариационный ряд, заданный таблицей |
Начальный порядка k |
|
|
Центральный порядка k |
|
|
Таблица 3
Неизвестный параметр |
Условия оценки |
Вид используемого распределения |
Границы интервала |
Доверительный интервал |
|
Математическое
ожидание
|
|
|
m,
где
|
|
|
|
|
m,
где
|
|||
Дисперсия
|
|
|
|
|
|
- неизвестно |
распределение |
|
|
||
|
|
|
|||
Вероятность
|
|
- функция Лапласа |
p, где
|
|
|
Таблица 4.
№ п/п |
Тип гипотезы H0 |
Условия |
Границы критической области на уровне значимости |
Статистика наблюдений |
1 |
О числовом значении генерального среднего
M( |
- известно для N(m,σ) |
Функция Лапласа Ф(uкр)= |
|
- неизвестно для N(m,σ) |
Распределение Стьюдента St с k=n-1 степенями свободы |
|
||
2 |
О числовом значении дисперсии
M( |
|
Распределение с k=n-1 степенями свободы |
|
3 |
Сравнение дисперсий двух совокупностей
DX=DY
или
|
XN(m1,1) YN(m2,2) s1>s2 |
Распределение Фишера-Снедекора с k1=n1-1 и k2=n2-1 степенями свободы |
|
4 |
Сравнение средних двух совокупностей
|
XN(m1,1) YN(m2,2)
|
Функция Лапласа Ф(z) Z-нормированная нормальная СВ |
|
|
Распределение Стьюдента с k=n1+n2-2 степенями свободы |
|
||
5 |
Сравнение относительной частоты с гипотетической вероятностью p=p0 |
|
Функция Лапласа Ф(u) |
|
6 |
О законе распределения (критерий согласия гипотезы о теоретическом распределении с опытными данными) |
r-число параметров теоретического распределения, вычисленных по выборке |
Распределение с k=s-r-1 степенями свободы, где s-число интервалов группировки |
|
Таблица 5
№ п/п |
Виды альтернативных гипотез H1 |
Критерий
отклонения H0
по статистике
|
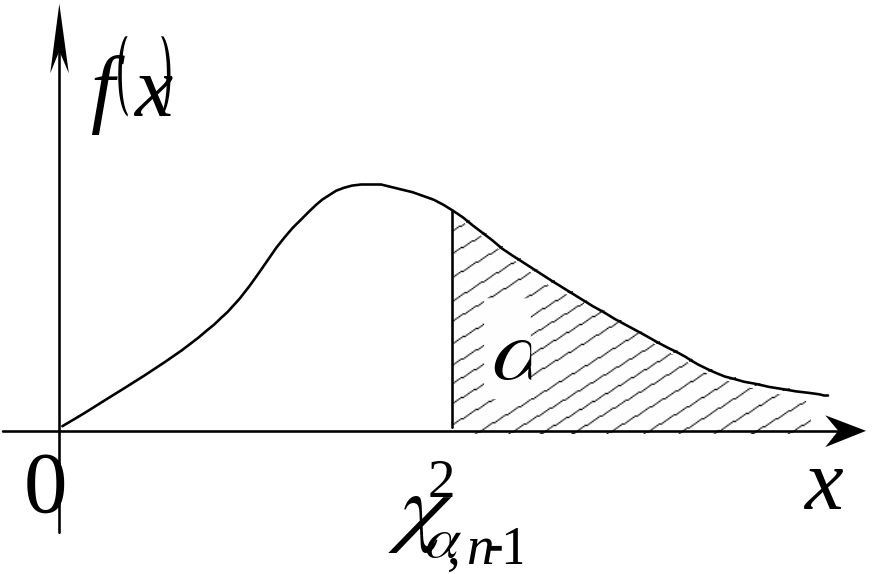
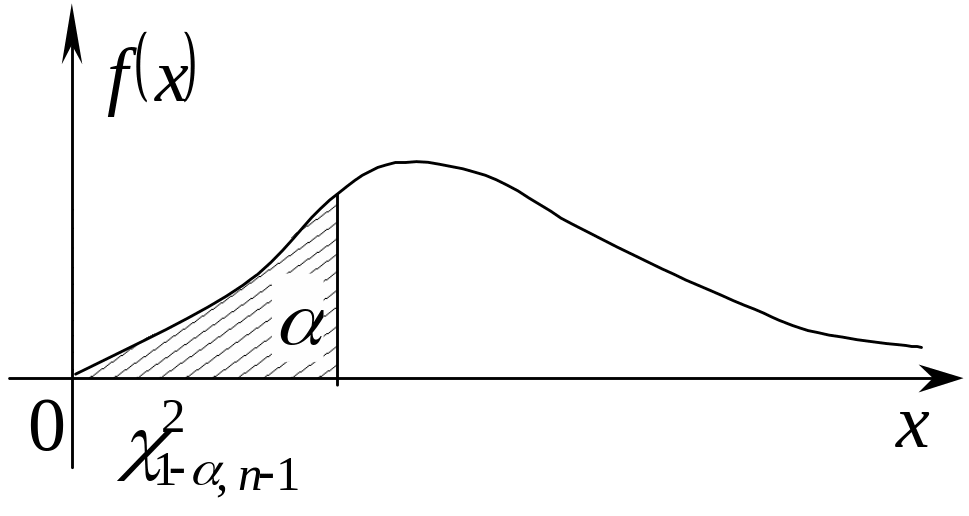
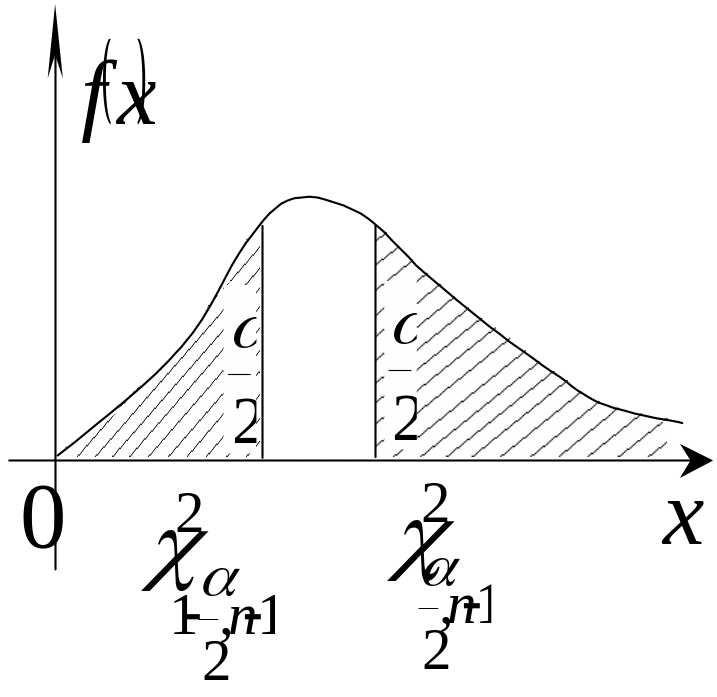
Графическая иллюстрация для |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|