
- •Приложение 3 Алгоритмы решения ключевых задач
- •II. Комплексные умения и алгоритмы к разделу 2 «Дискретные и непрерывные случайные величины»
- •III. Комплексные умения и алгоритмы к разделу 3 «Элементы математической статистики»
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Вычисление вероятности событий по определению Задача № 2-а. Студент знает ответы на 18 вопросов зачета из 30. Какова вероятность того, что он вытащит на зачете известный ему вопрос? Решение:
- •Вычисление вероятностей событий с помощью соединений
- •Вычисление вероятности события a по формуле полной вероятности. Вычисление вероятности одной из гипотез по формуле Байеса. Задача № 5.
- •Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Бернулли
- •Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Пуассона
- •Алгоритм № 8
- •Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли.
- •Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании
- •Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов гипергеометрических распределений
- •Вычисление числовых характеристик нсв,
- •Вычисление числовых характеристик нсв, равномерно распределенной на отрезке [a,b], а также вероятность
- •Вычисление числовых характеристик нсв, имеющей показательное распределение на отрезке [a,b]
- •III. Комплексные умения и алгоритмы к
- •Разделу 3 «Элементы математической статистики»
- •Алгоритм на умение №18
- •Построение вариационного ряда, эмпирической функции распределения и ее графика - кумуляты.
- •Алгоритм на умение №2/19 Построение полигона и гистограммы
- •Алгоритм на умение №4/21 Вычисление точечной несмещенной оценки для дисперсии
- •Алгоритм на умение № 5/22
- •Алгоритм на умение №6/23
- •Вычисление доверительных интервалов для математического
- •Ожидания m нормального распределения
- •Задача 23.
- •Алгоритм на умение №7/24
- •Вычисление доверительных интервалов для генеральной
- •Дисперсии d и среднеквадратичного отклонения
- •Задача 24.
- •Алгоритм на умение №8/25 Вычисление доверительного интервала для вероятности р наступления события а с помощью таблиц нормального распределения
Вычисление числовых характеристик нсв, равномерно распределенной на отрезке [a,b], а также вероятность
попадания НСВ Х в интервал P(a< Х < b)
Задача 14. Случайная величина Х — время ожидания дождя в течение суток — имеет равномерное распределение на отрезке [0, 20]. Найти математическое ожидание M(X), дисперсию D(X), функцию распределения, а также вероятности Р(Х<5) и Р(Х>3).
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
|
Записать функция плотности вероятности f(x), определив границы интервала a и b. |
f(x)
=
|
|
|
Вычислить математическое ожидание MX по формуле для равномерных распределений MX= |
MX= |
|
|
Вычислить дисперсию DX по формуле для равномерных распределений . |
DX= |
|
|
Записать
функцию распределения вероятности
F(X),
имеющую вид F(X)= |
F(X)= |
|
|
Вычислить вероятности попадания НСВ в интервал P(a< Х < b) по алгоритму 13 (п.6). |
Р(Х<5)
=
P(X>3)
=
|
Алгоритм на умение № 15.
Вычисление числовых характеристик нсв, имеющей показательное распределение на отрезке [a,b]
Задача 15. Вероятность безотказной работы прибора в течение х часов равна е- 0.0002Х. Х- момент отказа прибора. Найти математическое ожидание M(X) - среднюю наработку на отказ Т и вероятность безотказной работы прибора в течение 500 часов.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
|
Записать функцию плотности вероятности f(x) показательного распределения по формуле
f(x)
=
. |
f(x)
=
|
|
|
Записать функцию распределения F(x) показательного распределения по формуле F(x) = |
F(x)
= |
|
|
Вычислить математическое ожидание. |
M(X)= |
|
|
Вычислить дисперсию и среднеквадратичное отклонение. |
D(Х)= |
|
|
Вычислить вероятность попадания в интервал по формуле P(a<X<b)= . |
Р(Х>500) = е-0.0002∙500 = е-0.1 = 0.905. |
Алгоритм на умение № 16.
Определение числовых характеристик и вероятности попадания нормально распределенной НСВ Х в интервал P(a< Х < b)
Задача№ 16-а. Случайная величина Х имеет нормальное распределение
N(m,σ) = N(3,2). Найти числовые характеристики, функцию распределения, плотность вероятности НСВ Х, а также вероятности попадания НСВ Х в интервалы P(-1 < Х < 1), P(- 2 < Х-3 < 2), P(-4 < Х-3 < 6).
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
|
Записать математическое ожидание m, дисперсию D и среднеквадратичное отклонение σ для нормально распределенной СВ. |
m=MX=3, σ==2, D(X)=22= 4.
|
|
|
Записать
функцию распределения F(X)= |
Функция
распределения имеет вид F(X)= |
|
|
Вычислить P(-1<x<1), используя таблицы 3, по формуле P(a<x<b)=Ф( )-Ф( ). |
P(-1 < Х < 1) =
=
= -0.34338-(-0.4772)= 0.1334. |
|
|
Вычислить P(- 2< x-3 < 2) или Р(|x-3|<2) по формуле P(|x-a|<)=2Ф( ), используя таблицы 3 (Приложение 1). |
P(-
2 < х-3
< 2) = Р(|x-3|<2)=2Ф( |
|
|
Вычислить P(-4<Х-3<6) используя таблицы 3, по формуле P(a<x<b)=Ф( )-Ф( ). |
P(-4<Х-3<6)=Р(-1<x<9)=Ф( = Ф(3) – Ф(-2) = 0.9986 – 0.0228 = 0.9758. |
|
|
Вычисляется P(-6 <Х-3 < 6) с помощью правила трех «сигм» |
P(-
6 < Х-3
< 6) = Р(
= Ф(3) – Ф(-3) = 0.9986 – 0.0014 = 0.9972. |
Задание 16-б. Вес
цемента, упакованного автоматом в
бумажный мешок, есть случайная нормально
распределенная величина с математическим
ожиданием m=
50 кг и среднеквадратичным отклонением
![]() кг
(заданный стандарт x=
кг
(заданный стандарт x=![]() кг).
Найти вероятность того, что: а) случайно
выбранный мешок будет содержать не
менее 48 кг цемента; б) партия из 100 мешков
будет содержать не более 5040 кг.
кг).
Найти вероятность того, что: а) случайно
выбранный мешок будет содержать не
менее 48 кг цемента; б) партия из 100 мешков
будет содержать не более 5040 кг.
Решение
№ п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму |
1. |
Записать условие символически: математическое ожидание mX, среднеквадратичное отклонение , дисперсия DX. |
а) М(Х)=m=50, =2, D(X) = 4, б) Пусть СВ Y – вес 100 мешков цемента, тогда
Найти а) P(48), б) (<5040) |
2. |
Вычислить вероятности попадания в интервал с помощью таблиц нормального распределения (функция Лапласа, табл.3 Приложение 1). |
а) б) Замечание: использовали свойство нечетной функции Лапласа: Ф(-х)=-Ф(х). |
Алгоритм на умение 17
Оценить с помощью неравенства Чебышева вероятность того, что НСВ отличается от среднего на величину
Задача 17-а. Вес мужчины — случайная величина со средним 80 кг и дисперсией 50 кг2. Оценить с помощью неравенства Чебышева вероятность того, что вес случайно встреченного мужчины отличается от среднего на величину a)больше, чем 10 кг, б) не больше, чем 15кг.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
|
Записать условие символически: математическое ожидание m, дисперсия DX, оценка отклонения . |
m=80; DX=50, a)1=10, б) 2=5 |
|
|
Подставить значения mX, DX и в неравенство Чебышева P ( |X – m | ≥ ) ≤ , т.к. надо оценить вероятность того, что НСВ отличается от среднего на величину, больше, чем . |
а)Из неравенства Чебышева следует
P
( |X
- 80
| ≥ 10
) ≤
|
|
|
Подставить значения mX, DX и в неравенство Чебышева P ( |X – m | < ) ≥1- , т.к. надо оценить вероятность того, что НСВ отличается от среднего на величину, меньше, чем . |
б)Из неравенства Чебышева следует
P
( |X
- 80
| <15)
≥1- |
.
№ |
Умение |
Алгоритмы |
||||||||||||||||
1/18 |
Построение вариационного ряда, эмпирической функции распределения и ее графика - кумуляты. |
1. Для построения точечного вариационного ряда расположить заданные значения варианты xi в порядке возрастания, одинаковые значения объединить и найти их соответствующие частоты. Точечный вариационный ряд абсолютных частот примет вид:
2.Найти
их соответствующие относительные
частоты (статистические вероятности)
Вариационный ряд относительных частот примет вид:
3. Составить эмпирическую функцию распределения, для чего найти накопительные частоты (плотность вероятности) на каждом интервале, просуммировав их по формуле:
4.
Для построения кумуляты начертить
декартову систему координат и отложить
на оси абсцисс все возможные значения
варианты x1,
x2,
… ,
xk,
а на оси ординат – соответствующие
значения функции F*(x)= 5. Построить график эмпирической функции распределения, состоящий из отрезков с ординатами pi, построенными на соответствующих интервалах 1 i k (для дискретных вариант) или соединить отрезками полученные точки (для непрерывных вариант). |
||||||||||||||||
2/19 |
Построение полигона и гистограммы |
1. Для построения вариационного ряда расположить заданные значения варианты xi в порядке возрастания, одинаковые значения объединить и найти их соответствующие частоты
2.
Одинаковые значения объединить и
найти их соответствующие частоты
(статистические вероятности) pi= Вариационный ряд относительных частот примет вид:
3.
Отложить на оси ординат абсолютные
частоты n1,n2,…,nk
или относительные частоты
, 4. Для построения графика полигона относительных (абсолютных) частот необходимо соединить полученные точки с координатами (x1, ), (x2, ), ... , (xn, ) [(x1, n1), (x2, n2), ... , (xn, nk)] отрезками прямых.
5.
Для построения интервального
вариационного ряда найти «размах»
выборки – ее границы, т.е.
6.Для построения гистограммы на оси ОХ откладываются полученные интервалы. Гистограмма состоит из прямоугольников, построенных на этих интервалах, высотами которых являются соответствующие этим интервалам значения частот (абсолютных или относительных).
Для составления вариационного ряда нужно: 1) найти минимальное и максимальное значения выборки — Хmin и Xmax; 2) в первой строке таблицы записать варианты данной генеральной совокупности (выборки) в порядке возрастания; 3) во второй строке записать значение частоты, соответствующей данной варианте.
|
||||||||||||||||
3/20 |
Вычисление точечной оценки параметров распределения по выборке. |
1. Построить вариационный ряд по алгоритму 18. 2. Вычислить числовые характеристики:
а
) выборочное среднее (несмещенная
оценка) :
3.
б) выборочную дисперсию (смещенная
оценка при n>30);
- для выборки, заданной вариационным рядом;
в)
выборочное среднеквадратичное
отклонение (смещенная
оценка при n>30)
|
||||||||||||||||
4/21 |
Вычисление точечной несмещенной оценки для дисперсии. |
1. Вычислить смещенную точечную оценку для дисперсии по формулам алгоритма 20.
2. Вычислить несмещенную точечную оценку для дисперсии по формуле:
3.
Вычислить несмещенную точечную
оценку для среднеквадратичного
отклонения
|
||||||||||||||||
5/22 |
Нахождение интервала, в который с заданной вероятностью попадает случайная величина, распределенная нормально или по Стьюденту с помощью статистических таблиц |
1. Выписать заданные в условии задачи значения или найти их по алгоритмам №20 и №21, формулу для интервала, а также используемые табличные значения, указав номер таблицы. 2. а) Пусть величина распределена нормально – N(m,) при 1.
Использовать
формулу P{
Так,
для =0.95
эта формула обращается в правило двух
сигм
(t0.95=2),
а для =0.997
– в правило трех
сигм
(t0.997=3):
б) Пусть величина распределена нормально – N(m,) при 0. Найти для значений = 0.05; 0.025; 0.005 использовать или таблицу 5, отыскивая в третьем столбце, или одну из соответствующих данному формул:
в) Величина задана распределенной по Стьюденту при 1.
Найти
tn,
из формулы
г) Величина задана распределенной по Стьюденту при 0.
Использовать
формулу
2. Выписать полученный интервал.
|
||||||||||||||||
6/23 |
Вычисление доверительных интервалов для математического ожидания m нормального распределения. |
1.Сосчитать выборочное среднее, выборочное среднеквадратическое отклонение (если не известно истинное). 2.Выписать нужную формулу доверительного интервала для математического ожидания m нормального распределения с уровнем доверия для случая, когда среднеквадратическое отклонение распределения а) известно:
б) неизвестно: Использовать вместо его эмпирическую оценку s с заменой в формуле доверительного интервала n на n-1 степеней свободы и вместо значений нормального распределения использовать значения tn-1, распределения Стьюдента с n-1 степенями свободы, содержащиеся в таблице 6:
или через несмещенную оценку s:
3.
Найти точность оценки по формуле
4.
Выписать полученный доверительный
интервал, пользуясь таблицами 5, 6 или
7 (Приложение 1), вычислив границы
требуемого в задании интервала по
формуле
|
||||||||||||||||
7/24 |
Вычисление доверительного интервала для генеральной дисперсии D и среднеквадратичного отклонения |
1. Выписать формулу, заданные в условиях задачи значения. 2. Найти пограничные значения вероятности для .=1-=0.1.
3.Найти
по таблицам
4.
Найти значения для
как
5.
Вычислить границы интервала по формуле
6. Выписать полученный доверительный интервал. |
||||||||||||||||
8/25 |
Вычисление доверительного интервала для вероятности р наступления события А с помощью таблиц нормального распределения. |
1.Вычислить
оценку
2. Найти доверительный интервал для р по формуле:
3. Для проверки гипотезы, сформулировать вывод из эксперимента, провести вычисления с доверительным интервалом. |

 .
.
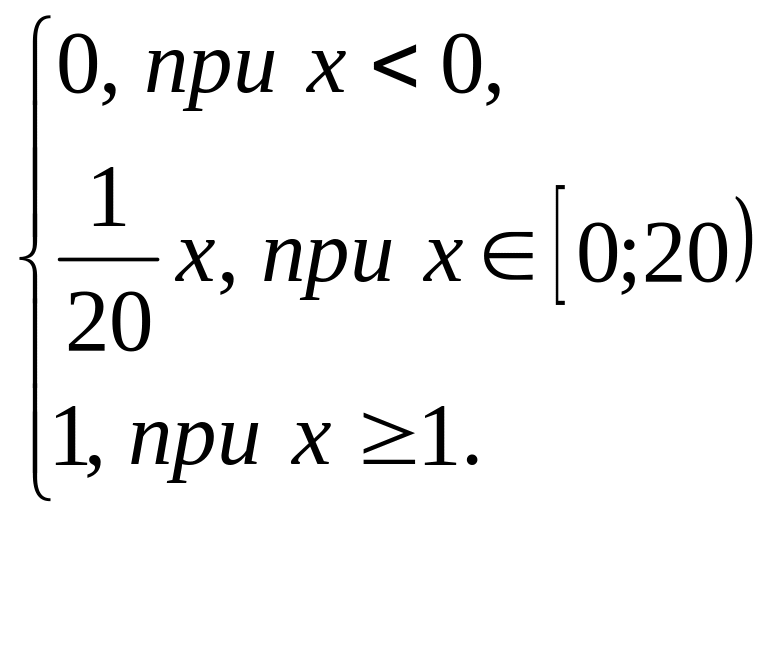 ,
,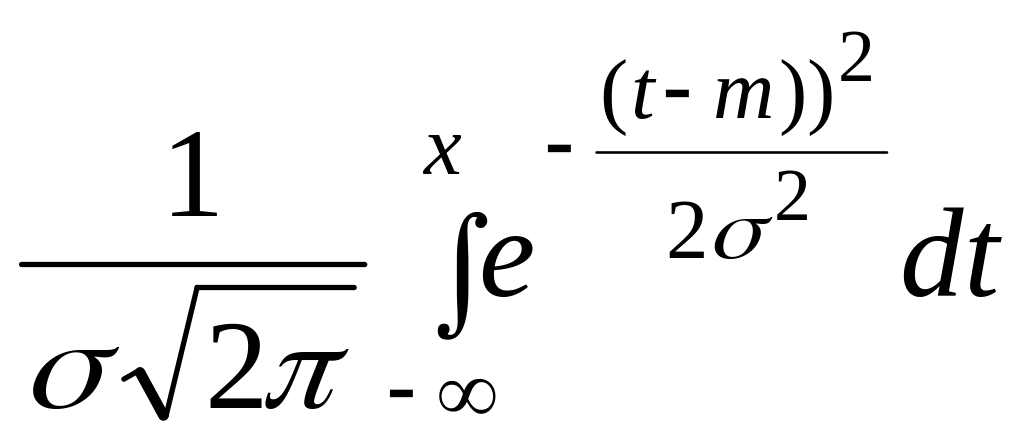 и плотность вероятности НСВ Х f(X)=
и плотность вероятности НСВ Х f(X)= .
.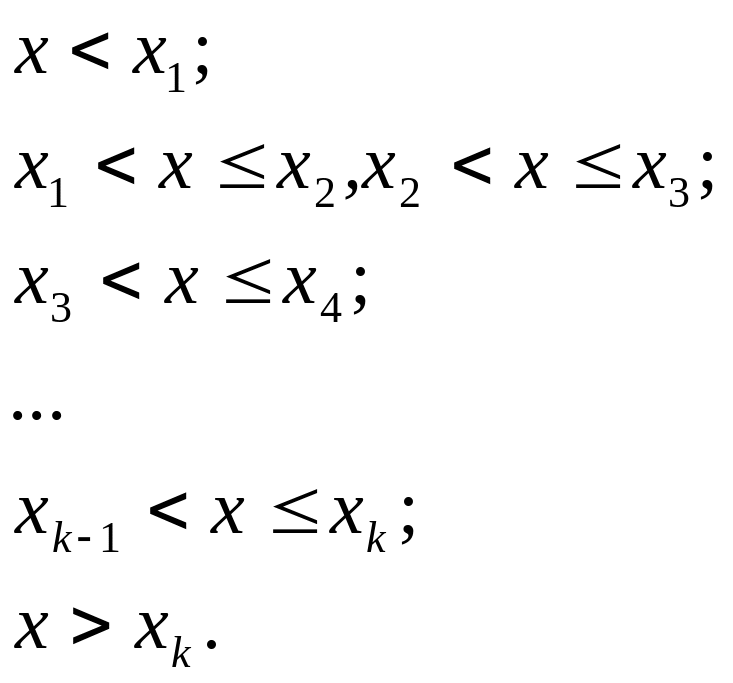 .
.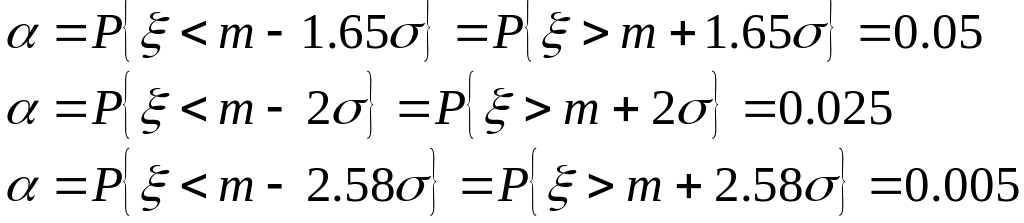
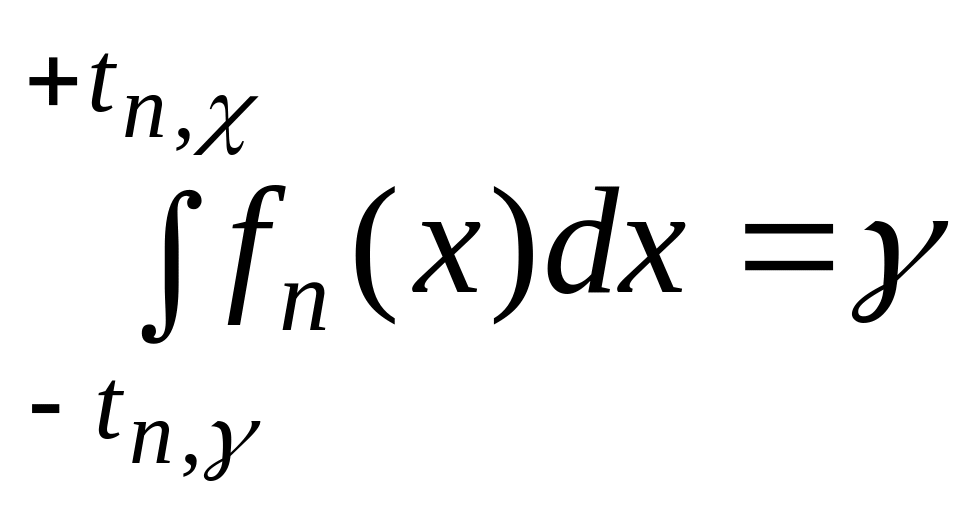 по таблице 6, отыскивая нужное
в верхней строке таблицы, а tn,
в строке, соответствующей данному n.
по таблице 6, отыскивая нужное
в верхней строке таблицы, а tn,
в строке, соответствующей данному n.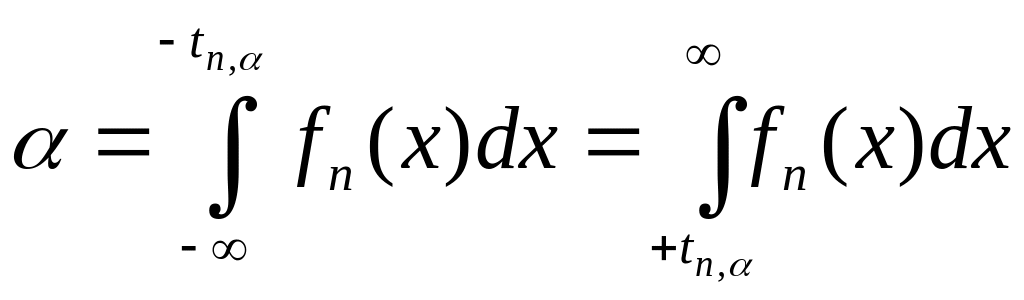 и найти tn,
с помощью таблицы 6, отыскивая нужное
в нижней строке таблицы, а tn,
в строке, соответствующей данному n.
и найти tn,
с помощью таблицы 6, отыскивая нужное
в нижней строке таблицы, а tn,
в строке, соответствующей данному n.