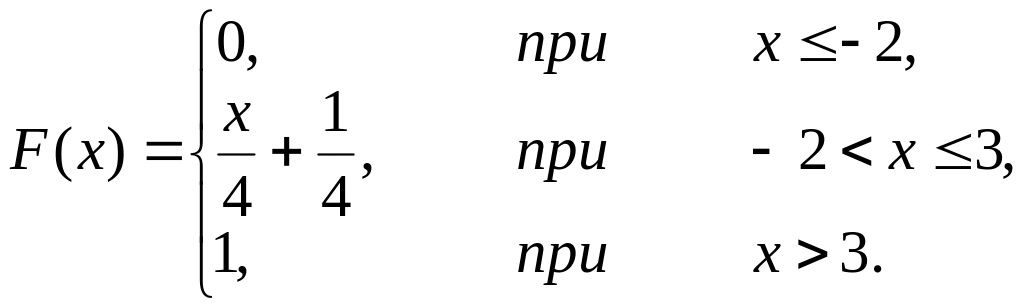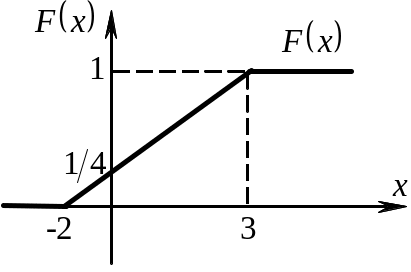- •Приложение 3 Алгоритмы решения ключевых задач
- •II. Комплексные умения и алгоритмы к разделу 2 «Дискретные и непрерывные случайные величины»
- •III. Комплексные умения и алгоритмы к разделу 3 «Элементы математической статистики»
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Вычисление вероятности событий по определению Задача № 2-а. Студент знает ответы на 18 вопросов зачета из 30. Какова вероятность того, что он вытащит на зачете известный ему вопрос? Решение:
- •Вычисление вероятностей событий с помощью соединений
- •Вычисление вероятности события a по формуле полной вероятности. Вычисление вероятности одной из гипотез по формуле Байеса. Задача № 5.
- •Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Бернулли
- •Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Пуассона
- •Алгоритм № 8
- •Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли.
- •Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании
- •Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов гипергеометрических распределений
- •Вычисление числовых характеристик нсв,
- •Вычисление числовых характеристик нсв, равномерно распределенной на отрезке [a,b], а также вероятность
- •Вычисление числовых характеристик нсв, имеющей показательное распределение на отрезке [a,b]
- •III. Комплексные умения и алгоритмы к
- •Разделу 3 «Элементы математической статистики»
- •Алгоритм на умение №18
- •Построение вариационного ряда, эмпирической функции распределения и ее графика - кумуляты.
- •Алгоритм на умение №2/19 Построение полигона и гистограммы
- •Алгоритм на умение №4/21 Вычисление точечной несмещенной оценки для дисперсии
- •Алгоритм на умение № 5/22
- •Алгоритм на умение №6/23
- •Вычисление доверительных интервалов для математического
- •Ожидания m нормального распределения
- •Задача 23.
- •Алгоритм на умение №7/24
- •Вычисление доверительных интервалов для генеральной
- •Дисперсии d и среднеквадратичного отклонения
- •Задача 24.
- •Алгоритм на умение №8/25 Вычисление доверительного интервала для вероятности р наступления события а с помощью таблиц нормального распределения
Вычисление числовых характеристик нсв,
а также вероятность попадания НСВ Х в интервал P(a< Х < b)
Задача 13-а. Функция плотности случайной величины Х имеет вид:
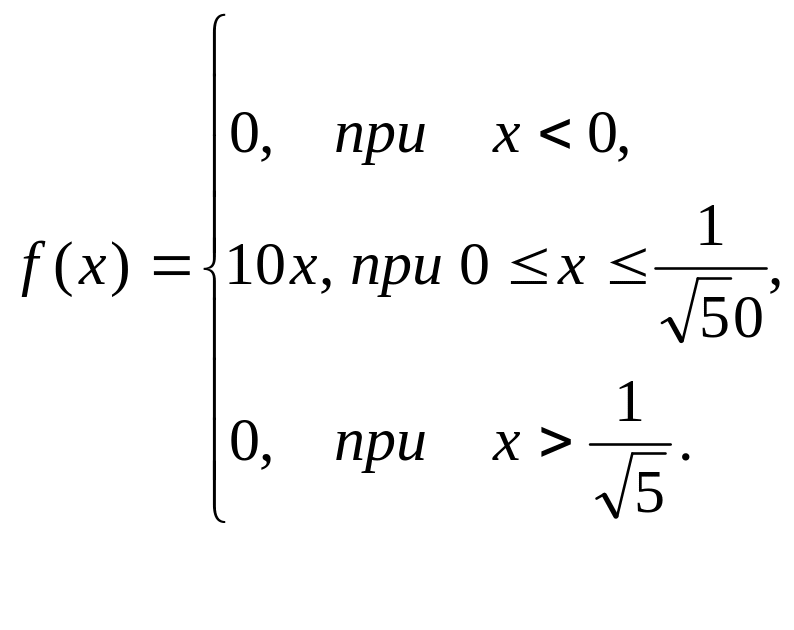

Найти
математическое ожидание M(X),
дисперсию D(Х),
а также вероятность попадания СВ Х в
интервал
P(0<
Х
< 0.1).
![]()
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
|
Записать функцию плотности вероятности f(x)=F|(x). Вычислить математическое ожидание на указанном отрезке. |
Функцию
плотности
вероятности
f(x)
задана.
Найдем
математическое
ожидание MX=
|
|
|
Вычислить дисперсию DХ и среднеквадратичное отклонение X. |
DХ
=
=
10 DХ=0.01, |
|
|
Вычислить P(0 < Х < 0.2). |
P(0<Х<0.2)
=
|
Задача 13-б. НСВ X задана функцией распределения
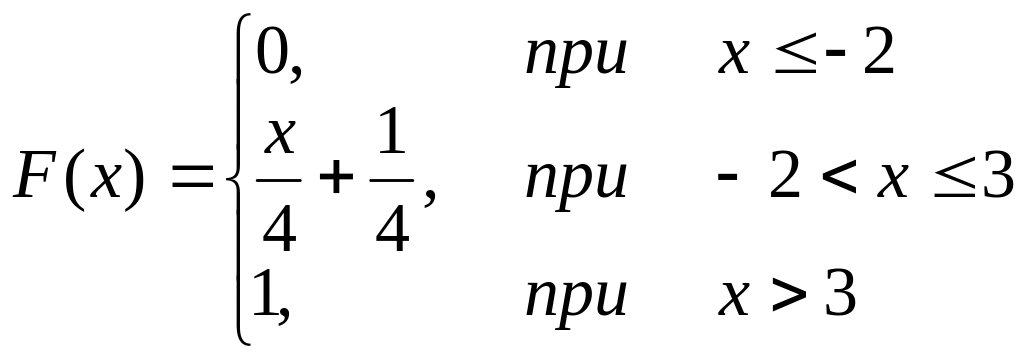 .
.
Найти:
1) плотность вероятности f(x);
2) числовые характеристики НСВ X;
3) вероятность того, что в результате испытаний СВ X примет значение в интервале(0;2);
4) графики функции распределения и плотности вероятности.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
1. |
Записать функцию плотности вероятности f(x)=F|(x). |
|
2. |
Вычислить математическое ожидание на указанном отрезке
|
. |
3. |
Вычислить дисперсию D(Х) и среднеквадратичное отклонение X |
DХ
=
=
|
|
|
Найти моду, исследовав на экстремум функцию f(x). |
Т.к.
|
|
|
Найти медиану Me, решив уравнение
|
Для
поиска медианы решим уравнение
|
|
|
Вычислить вероятность попадания в интервал (a;b) по формуле: P(a< Х < b)=Ф(b)-Ф(а). |
Найти вероятность попадания в интервал (a;b):
P(0<Х<2)
=
|
|
|
Построить график функции функции распределения
|
Функция распределения
Ее график имеет вид:
|
|
|
Построить график функции функции плотности вероятности.
|
Функция плотности вероятности
|
Алгоритм на умение № 14

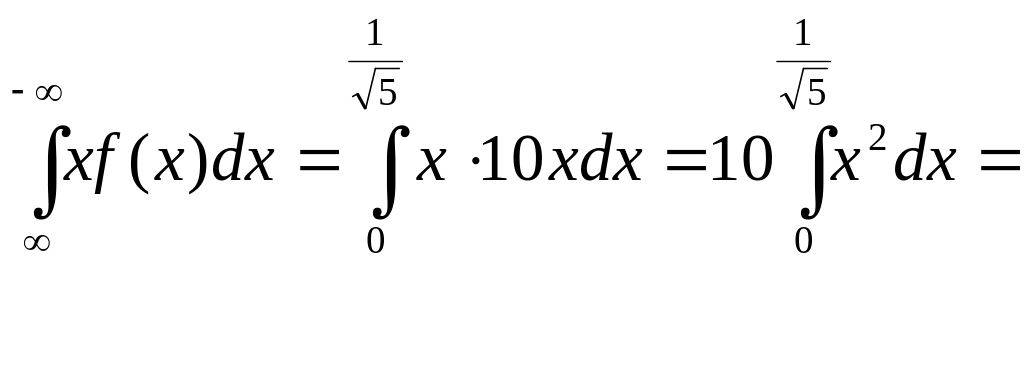
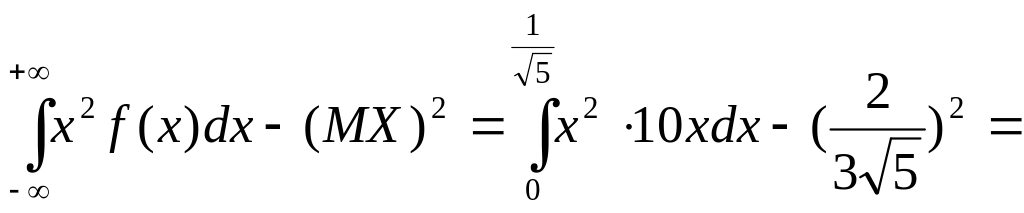
 ,
,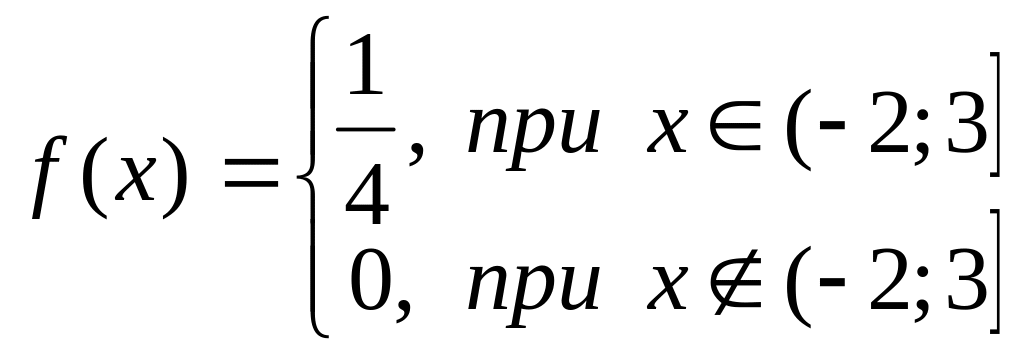 .
.