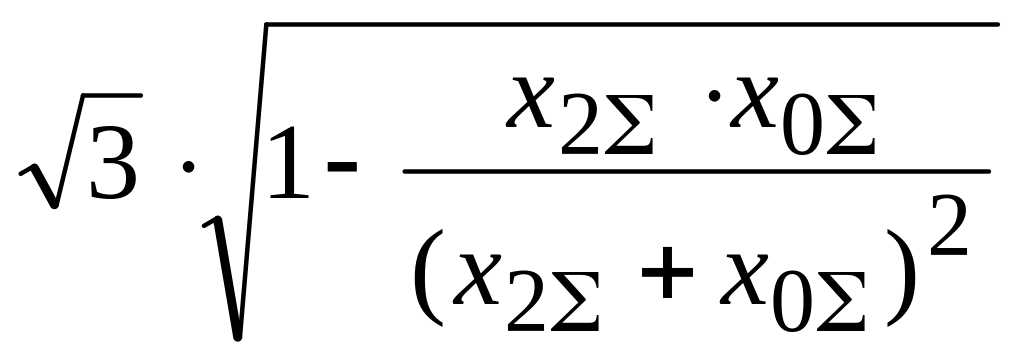Тема №9: «Однократная поперечная несимметрия»

1. Основные математические соотношения для различных видов КЗ (К⁽¹⁾; К⁽²⁾; К^(1,1)).

2. Векторная диаграмма токов и напряжений в месте КЗ.

3. Правило эквивалентности прямой последовательности.

4. Комплексные схемы замещения.

5. Распределение и трансформация токов и напряжений отдельных последовательностей.

6. Сравнение различных видов КЗ.

Литература: Л1 – с. 315-348, Л2 – с. 142-163, Л3 – с. 148-168.

1.1 Однофазное КЗ (К⁽¹⁾).

Рисунок 9.1

В соответствии со схемами замещения прямой, обратной и нулевой последовательности:

;

;

.

Граничные условия:

;

;

.

По методу симметричных составляющих:

;

;

.

Из этой системы с учетом граничных условий:

;

;

.

; – для особой фазы.

Полный ток КЗ:

;

.

Просуммируем левые и правые части первых трех уравнений:

;

. (*)

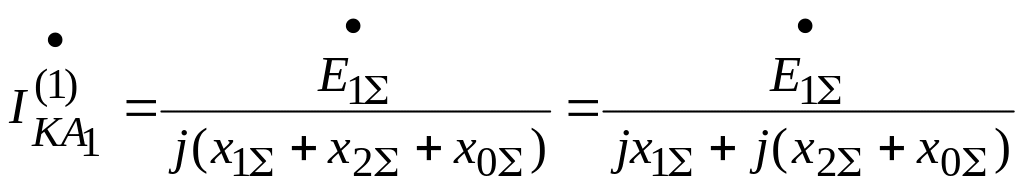Подставим значение ЭДС из уравнения (*) в первое уравнение:

;

;

;

.

1.2 Двухфазное КЗ на землю (К^(1,1)).

Рисунок 9.2

Первые три уравнения те же.

Граничные условия:

;

;

.

;

;

;

;

.

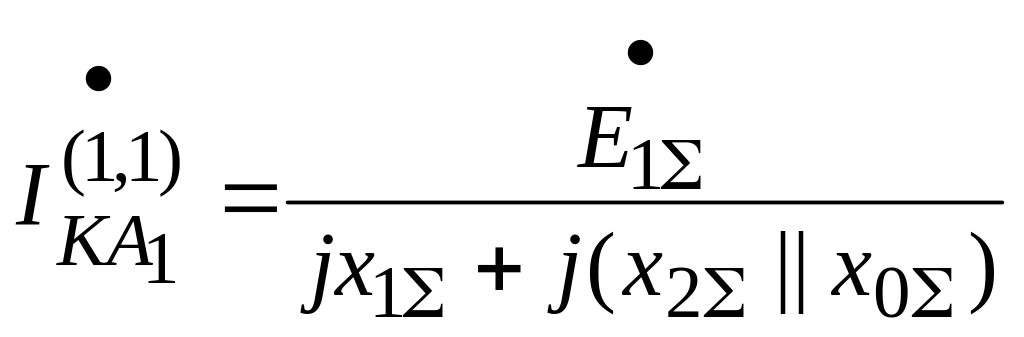Полный ток КЗ:

;

;

.

1.3 Двухфазное КЗ (К⁽²⁾).

Рисунок 9.3

Граничные условия:

;

;

; (*)

.

Токи нулевой последовательности исчезнут, что соответствует , (так как сумма фазных токов равна нулю, то система является уравновешенной и ). При этом ток фазы А: .

Откуда .

Из условия (*) и формул , имеем:

;

;

.

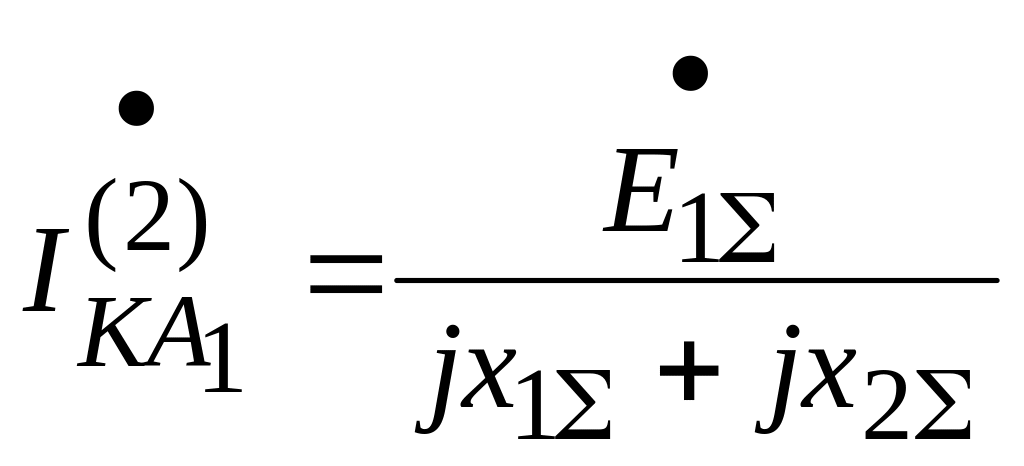Полный ток КЗ:

.

2. Векторные диаграммы в точке КЗ строятся следующим образом:

а) записываются соотношения симметричных составляющих токов или напряжений для определенного вида КЗ;

б) указанные соотношения изображаются в виде векторов для особой фазы;

в) достраиваются симметричные составляющие токов или напряжений;

г) для каждой фазы суммируются отдельные составляющие.

Например: однофазное КЗ; векторная диаграмма токов.

.

Рисунок 9.4

3. Аналогичность выражений для определения токов прямой последовательности, напряжений прямой последовательности и полного тока КЗ позволяет записать эти выражения для любого вида КЗ в общем виде (справедливо для любого момента времени):

;

где – дополнительное сопротивление, величина которого зависит от вида КЗ и определяется по таблице 9.1.

;

;

где – коэффициент, который определяется по таблице 9.1.

Таблица 9.1

Вид КЗ
К(1)		3
К(1,1)
К(2)
К(3)	0	1

Правило эквивалентности прямой последовательности (справедливо для основной гармоники тока несимметричного КЗ) – т.е. правило Щедрина Н.Н.: ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительное сопротивление , которое не зависит от параметров схемы прямой последовательности и для каждого вида КЗ определяется результирующими сопротивлениями обратной и нулевой последовательности относительно рассматриваемой точки схемы.

Чтобы найти ток несимметричного КЗ в точке К⁽ⁿ⁾, надо добавить сопротивление и за этим сопротивлением найти ток трехфазного КЗ. Этот ток является током прямой последовательности в данной точке.

Рисунок 9.5

4. Полученные выражения для соотношения токов и напряжений отдельных последовательностей позволяют объединить отдельные схемы в единую комплексную схему замещения.

Рисунок 9.6

Схема замещения для трехфазного КЗ (для прямой последовательности – с ЭДС; для обратной и нулевой – без ЭДС).

Комплексные схемы замещения даны на рисунках .

Все полученные ранее соотношения справедливы только для точки КЗ.

5. Для определения токов в любой ветви схемы или напряжений в любом узле необходимо предварительно в пределах схем различных последовательностей найти симметричные составляющие токов и напряжений в соответствующих ветвях и узлах, после чего, в соответствии с методом симметричных составляющих просуммировать соответствующие величины.

В схеме замещения прямой последовательности направления тока от источников к месту КЗ; в схемах обратной и нулевой последовательностей – от места КЗ к началу схем, так как ЭДС нет. В месте КЗ напряжение прямой и обратной последовательностей равны ( ).

Рисунок 9.7

.

Рисунок 9.8 – Прямая последовательность

.

Рисунок 9.9 – Обратная последовательность

.

Рисунок 9.10 – Прямая последовательность

По мере удаления от места КЗ и приближения к источнику напряжение прямой последовательности увеличивается, а обратной и нулевой уменьшается.

Для построения векторной диаграммы в любой точке системы необходимо взять соответствующие составляющие из эпюр. При этом необходимо учитывать, что в общем случае при трансформации токов и напряжений происходит сдвиг по фазе трансформируемых величин.

Рассмотрим особенности трансформации отдельных последовательностей через трансформатор (по ГОСТ 11677-85 установлены схемы и группы соединения обмоток высшего (ВН), среднего (СН) и низшего (НН) напряжения и угловое смещение векторов линейных ЭДС обмоток СН и НН по отношению к векторам ЭДС обмоток ВН. Группа соединения (угловое смещение) обозначается числом, которое при умножении на дает угол отставания в градусах ( ).

Иначе говоря, при переходе через трансформатор , прямая последовательность поворачивается на в направлении противоположном направлению вращения часовой стрелки; обратная последовательность на угол по часовой стрелке; нулевая не выходит из трансформатора; при переходе через трансформатор в обратном направлении угловые смещения симметричных составляющих меняют свой знак на противоположный.

Рисунок 9.11 – Векторная диаграмма токов для К1⁽²⁾

При соединении линейные токи за треугольником не содержат составляющих нулевой последовательности.

Рисунок 9.12

Наиболее простые соотношения получаются для трансформатора с соединением обмоток по группе 12, так как в этом случае угловые смещения токов и напряжений вообще отсутствуют. При этом когда имеется соединение , должны быть учтены трансформируемые составляющие нулевой последовательности.

Рисунок 9.13 – Сдвиг векторов напряжений прямой и обратной последовательностей для трансформатора с соединением обмоток

При нечетной группе соединения обмоток (например, по группе 3 или 9) векторы прямой и обратной последовательностей повернуты на в противоположные стороны (рис.9.14).

Рисунок 9.14

Очевидно, векторы прямой последовательности можно оставить без смещения, а векторы обратной последовательности нужно сдвинуть на . Отсюда правило: при переходе через трансформатор с соединением обмоток по схеме или достаточно только у векторов обратной последовательности изменить знак на противоположный. Если токи и напряжения выражены в относительных единицах, то при их трансформации должны учитываться лишь угловые сдвиги, обусловленные соответствующей группой соединения обмоток трансформатора.

При построении векторных диаграмм напряжений для различных участков сети следует учитывать:

а) напряжение прямой последовательности имеет наименьшее значение в месте КЗ и повышается при приближении к источнику; а напряжения обратной и нулевой последовательностей, наоборот, имеют наибольшие по модулю значения в месте КЗ и уменьшаются при приближении к источнику;

б) при переходе через трансформатор системы векторов прямой и обратной последовательностей поворачиваются соответственно по ходу и против хода часовой стрелки относительно их положения в месте КЗ, причем угол поворота зависит от группы соединения обмоток трансформатора;

в) обмотки трансформаторов, соединенные в треугольник, ограничивают область прохождения токов нулевой последовательности в сети; в комплексных схемах они являются началом схемы нулевой последовательности.

Сравнение различных видов КЗ по величине тока.

Правило эквивалентности прямой последовательности и установленные значения и (табл. 9.1) позволяют достаточно точно сравнить различные виды КЗ (принимается условие: короткозамкнутая цепь чисто индуктивная).

Принимаем, что КЗ различных видов происходят поочередно в одной и той же точке системы в одинаковых исходных условиях; тогда с учетом табл. 9.1 можно записать:

.

Токи прямой последовательности:

.

Напряжения прямой последовательности:

.

Определим пределы, в которых могут находиться значения токов при несимметричных КЗ по сравнению со значениями токов трехфазного КЗ в той же точке системы; это позволяет по известному оценить возможные наибольшие и наименьшие значения тока при несимметричных КЗ (и это справедливо только для токов в месте КЗ).

Отношение тока в месте несимметричного КЗ к току трехфазного (для любого момента времени):

;

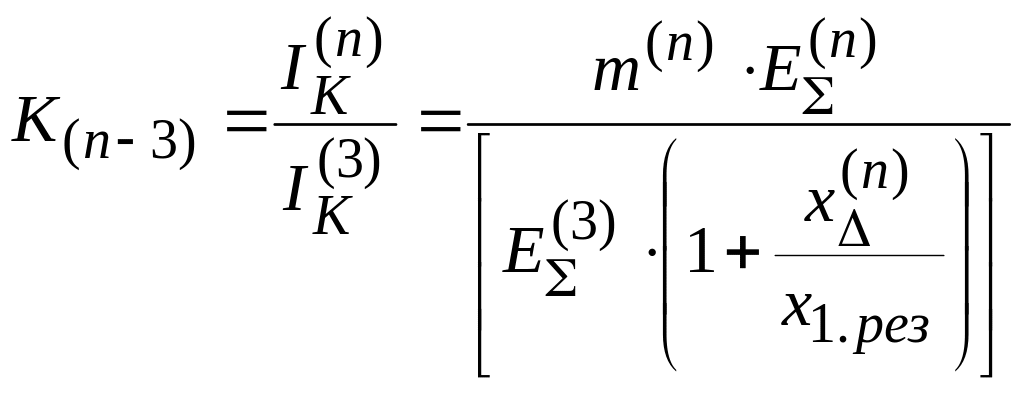где – вид КЗ.

При пренебрежении различием и получают:

.

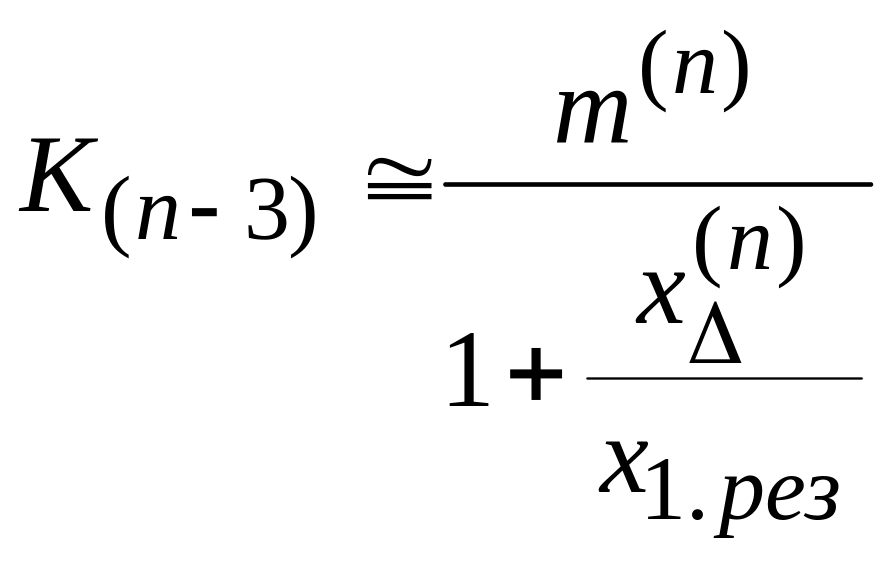Для начального момента времени = .

Двухфазные КЗ.

.

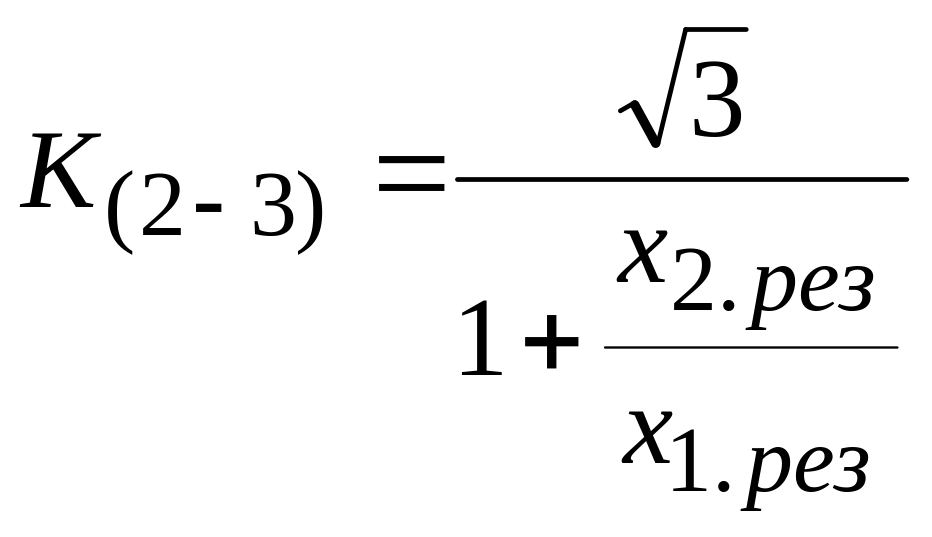Если КЗ вблизи зажимов генератора: ; при : ; ; значит ; ; в установившемся режиме ( ); ; ; ; т.е. можно принять ; тогда .

Значит .

При КЗ в удаленной точке – велико; т.е. (независимо от времени КЗ):

.

Тогда .

Однофазное КЗ.

Отношение токов:

.

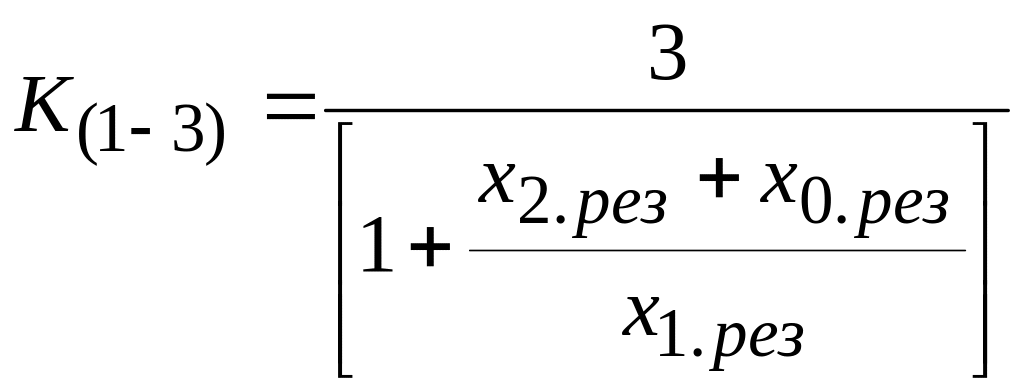Индуктивное сопротивление (изменяется в широких пределах; например, увеличением числа заземленных нейтралей трансформаторов с кВ). При КЗ вблизи зажимов генератора ( ), если , при установившемся КЗ, когда , то можно принять . Тогда ; если ; то .

Значит .

При КЗ в удаленной точке системы, где , при условиях (предельных) или , то

.

Двухфазное КЗ на землю.

Как и при двухфазном КЗ:

.

Т.е. можно определить примерные пределы, в которых могут быть величины токов при несимметричных КЗ по сравнению с током трехфазного КЗ в той же точке.