Обработка результатов измерений

1. По данным таблицы 6.1 рассчитать среднее значение времени десяти колебаний математического маятника.

2. Рассчитать среднее значение периода колебаний математического маятника по формуле

3. По формуле (6.9) вычислить значение ускорения свободного падения для широты С-Петербурга.

4. По данным таблицы 6.3 рассчитать средние значения 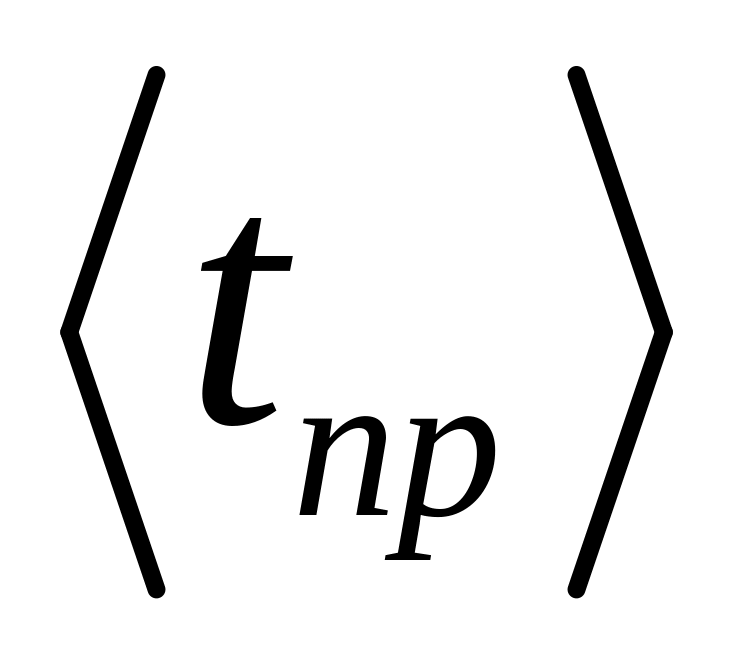и .

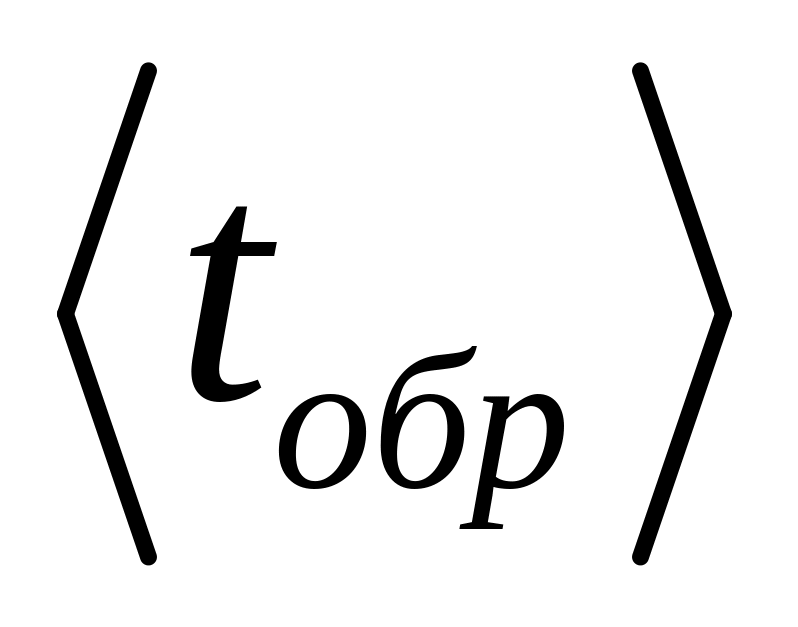5. Рассчитать средние значения периодов колебаний физического маятника в прямом 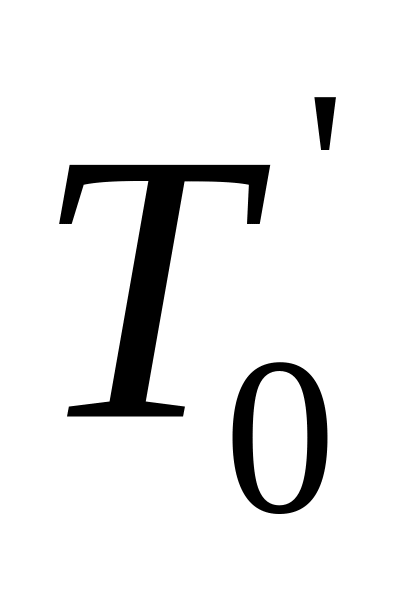и обратном 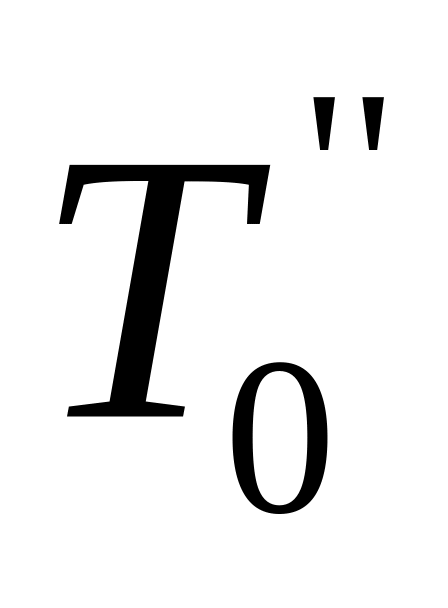положениях по формулам

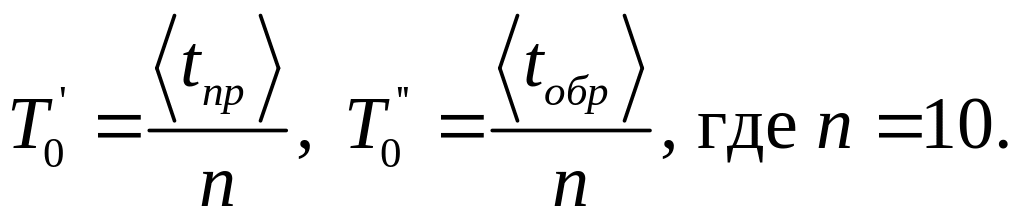
6. По формуле 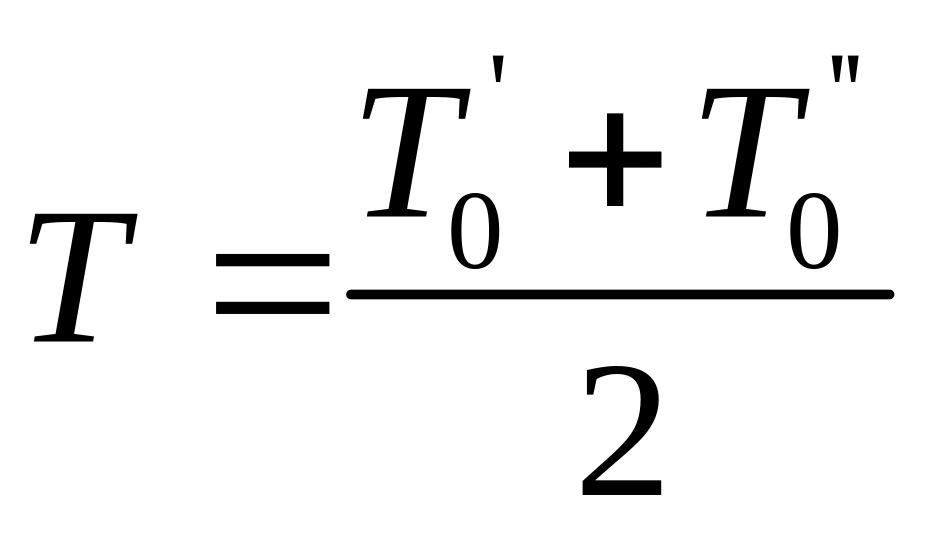найти среднее значение периода колебаний физического маятника.

7. По формуле (6.10) рассчитать значение ускорения свободного падения.

8. Рассчитать погрешность определения ускорения свободного падения как погрешность косвенного измерения.

9. Сравнить полученные значения с табличным значением ускорения свободного падения для широты С-Петербурга (g₀ = 9,82 м/с²).

Контрольные вопросы

1. Дать определения физического и математического маятников. Вывести периоды их собственных незатухающих колебаний.

2. Что называется приведённой длиной физического маятника?

3. Как зависит величина ускорения свободного падения от широты местности?

Литература: [2, § 36, 39, 41]; [4, § 27.2 ]; [5].

Лабораторная работа №7

Определение момента инерции маятника максвелла

Цель работы – вычисление момента инерции маятника Максвелла по измеренным кинематическим параметрам его движения и сравнение вычисленного значения с моментом инерции, полученным теоретическим расчетом. Проверка выполнения закона сохранения энергии.

Приборы и принадлежности: маятник Максвелла, блок миллисекундомера со счетчиком импульсов.

Краткие сведения из теории

Маятник Максвелла представляет собой диск, плотно насаженный на ось. Ось подвешена к неподвижному штативу на двух симметрично закрепленных параллельных вертикальных нитях одинаковой длины. Если нити намотать на ось и отпустить маятник, то под действием силы тяжести и силы натяжения нитей он движется вниз, одновременно вращаясь вокруг своей оси. В крайнем нижнем положении маятник продолжает вращаться по инерции, при этом нити опять наматываются на ось, но в направлении, противоположном первоначальному. Маятник, вращаясь вокруг своей оси, движется вверх. Таким образом, ось маятника совершает колебания в вертикальной плоскости. Однако подробное изучение движения маятника именно как колебательного процесса выходит за рамки данной работы.

В этой лабораторной работе для измерений и расчетов используется лишь первая фаза колебания: от момента отпускания маятника в верхней точке до прохождения им крайнего положения.

Вывод рабочей формулы для экспериментального определения момента инерции маятника

Движение маятника Максвелла является плоским, т.е. таким движением, при котором все точки тела перемещаются в параллельных плоскостях. Это движение можно представить как суперпозицию двух основных видов движения: поступательного со скоростью, равной скорости центра инерции тела, и вращательного вокруг оси, проходящей через центр инерции. Тогда движение маятника описывается двумя уравнениями: и , где m – масса маятника; – ускорение поступательного движения центра инерции; – равнодействующая всех сил, действующих на маятник; I – момент инерции маятника; – угловое ускорение вращательного движения маятника; – суммарный момент всех внешних сил. Величины I, M, вычисляются относительно оси OO₁, проходящей через центр инерции (рис.7.1). При записи уравнений предполагалось, что нить невесома и нерастяжима, а трение в точках подвеса пренебрежимо мало.

Рис. 7.1

Если первое из этих уравнений спроецировать на направление движения, а второе уравнение – на ось вращения, получим два скалярных уравнения: ma = mg – 2T, I = 2rT, где T – сила натяжения каждой нити, создающая вращающий момент. Если проскальзывание отсутствует, то линейное и угловое ускорение связаны соотношением: a = r. Совместное решение этих трех уравнений дает возможность найти момент инерции маятника:

I

Рис 18.1

= mr²(g/а – 1).

Расстояние от оси вращения до точки приложения силы натяжения r = r₁ + r_нити, где r₁ – радиус оси маятника.

Движение центра инерции маятника является поступательным и равноускоренным с нулевой начальной скоростью, следовательно: a =2h/t², где h – путь, который проходит центр инерции маятника за время t.

Окончательно рабочая формула для момента инерции маятника имеет вид

(7.1)

Кинетическая энергия в каждый момент времени при движении маятника . Учитывая, что и , получаем

. (7.2)