Вывод рабочей формулы для экспериментального определения момента инерции.

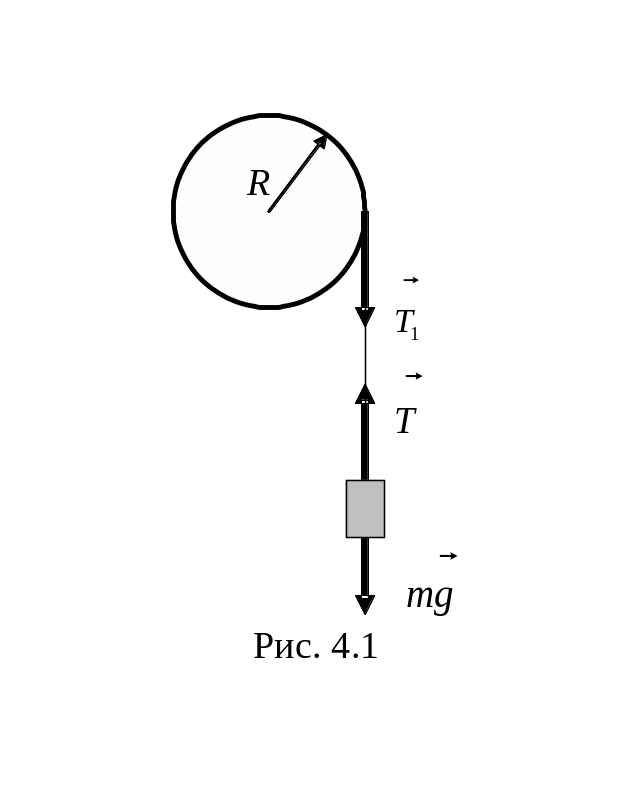
Рис. 4.1

При экспериментальном определении момента инерции используется маятник Обербека, который представляет собой крестовину с четырьмя закрепленными на ней на одинаковых расстояниях от оси одинаковыми грузами. На ось крестовины насажен двухступенчатый шкив, на который намотана нить с подвешенным к ней грузом. При движении груза вниз шкив начинает вращаться. Для вывода рабочей формулы рассмотрим упрощенную схему установки, выделив систему связанных движущихся тел: поступательно движущийся груз и вращающийся шкив (рис. 4.1). Поступательное движение груза описывается уравнением:

mg – T = ma (4.1)

Вращательный момент шкива создает сила натяжения нити Т₁, которая по третьему закону Ньютона равна силе Т. Этот момент М = ТR. Тогда уравнение вращательного движения шкива:

ТR=Iε (4.2)

Если отсутствует проскальзывание нити, то тангенциальное ускорение элементов нити, вращающихся вместе со шкивом, равно линейному ускорению груза:

а_τ = а = εR (4.3)

Решая систему уравнений (4.1), (4.2) и (4.3), получим для момента инерции выражение: .

Линейное ускорение груза можно вычислить по измеренным высоте падения груза и времени его падения: h=at²/2.

Таким образом, получена рабочая формула для экспериментального определения момента инерции:

(4.4)

Вывод формулы для теоретического вычисления момента инерции.

Момент инерции является аддитивной величиной, то есть момент инерции системы тел равен сумме моментов инерции всех тел, входящих в систему. Маятник Обербека состоит из шкива (включая ось и втулку крестовины), четырех стержней крестовины и грузов, укрепленных на крестовине. Момент инерции шкива указан на установке. Момент инерции стержня относительно оси, проходящей через его конец, равен m₂l_c²/3, где m₂ − масса стержня без груза, l_c − длина стержня крестовины − указаны на установке. Грузы, укрепленные на крестовине, приближенно можно считать за точечные массы. Тогда момент инерции каждого груза равен m₁l², где m₁ − масса одного груза (указана на установке), l − расстояние от оси вращения до центра масс груза (измеряется при выполнении работы).

Теоретический момент инерции после суммирования вычисляется по формуле:

I = I₀ + 4m₁l² + 4m₂l_c²/3 (4.5)

Описание экспериментальной установки

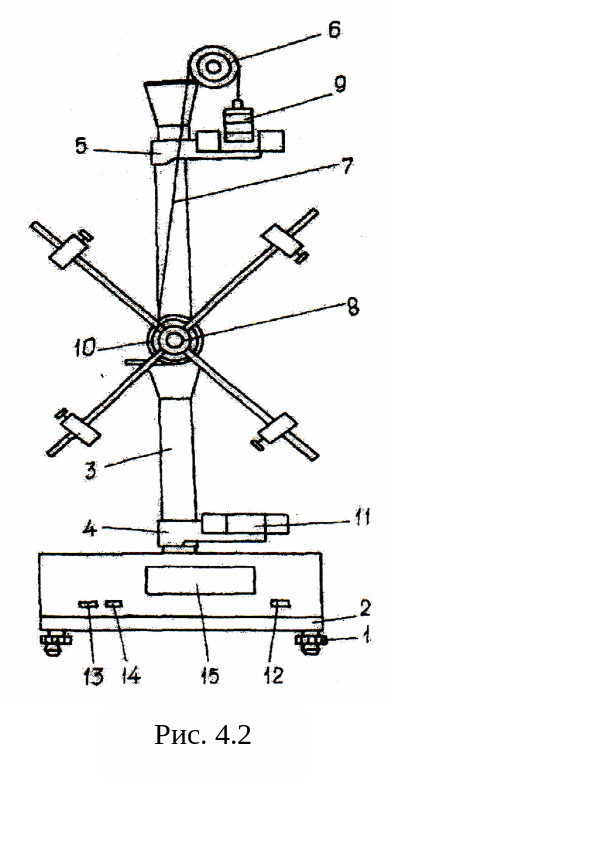
Рис. 4.2

Внешний вид установки представлен на рис.4.2. Регулировочные винты 1 обеспечивают горизонтальную установку основания 2, к которому крепится вертикальная колонка 3, на которой нанесена миллиметровая шкала. К этой колонке прикреплены неподвижный кронштейн 4 и верхний подвижный 5, с помощью которого можно регулировать длину пути груза h. Через диск 6 перекинута нить 7, один конец которой прикреплен к шкиву 8, а на втором конце закреплены грузы 9. Кронштейн 11 снабжен резиновым амортизатором для ограничения движения грузов. Включение прибора производится нажатием клавиши «сеть» 12, обнуление миллисекундомера производится клавишей «сброс» 13, клавиша «пуск» 14 включает миллисекундомер. Время падения груза высвечивается на индикаторе 15.