1. К. П. Д. Блоков отклоняющих.

О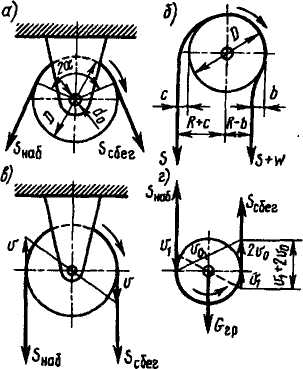 тклоняющим называется блок, который изменяет направление движения охватывающего каната. Отклоняющий блок, установленный неподвижно, называется неподвижным, а блок, перемещающийся в пространстве, называется подвижным.

На рис.5.23, а показан неподвижный блок, вращающийся по часовой стрелке под действием силы S_СБЕГ, преодолевающей силу S_НАБ. Вращение блока возможно только в том случае, если S_СБЕГ > S_НАБ, причем разность S_СБЕГ – S_НАБ должна быть достаточна для преодоления сопротивления сил трения в опоре блока и сопротивления жесткости каната или цепи при их сгибании и разгибании.

23. Блоки: а– блок с неподвижной осью; б– схема набегания каната на блок; в– схема скоростей каната на неподвижном блоке; г– схема скоростей каната на подвижном блоке

Так как канаты, применяемые в грузоподъемных машинах, не являются абсолютно гибкими телами, а имеют определенную жесткость, то набегающая ветвь каната не сразу ложится на ручей блока, а сбегающая ветвь не сразу выпрямляется (рис.5.23, б). Жесткость каната зависит от его диаметра, конструкции, числа проволок в прядях и числа прядей, от типа и конструкции сердечника, от механических свойств материала проволок и от трения между отдельными проволоками и между прядями. Жесткость цепи определяют в основном по сопротивлению сил трения в шарнирах пластинчатой цепи или сил трения между звеньями сварной цепи.

Для сгибания и разгибания каната к его сбегающей ветви необходимо приложить дополнительную силу W, которая зависит от размеров и конструкции каната и блока, а также от натяжения каната. Ее можно определить из уравнения моментов сил относительно оси блока (рис.5.23, б) без учета сил трения в опоре блока:

ΣМ_О=S (R+c)– (S+W) (R–b)=0,

S (R+c)= (S+W) (R–b),

W (R–b) = S (R+c) – S (R–b),

W = S = φS ,

где R = D/2 - радиус ручья блока; φ– коэффициент жесткости: его значение определяют экспериментально.

Уравнение моментов всех действующих сил относительно оси блока (рис.5.23, а) имеет такой вид:

ΣМ_О= S_НАБ R + W R + N f d₀ / 2 – S_СБЕГ R = 0,

S_СБЕГ R = S_НАБ R + φ S_НАБ R + N f d₀ / 2,

где N–- нагрузка на ось блока, равная геометрической сумме сил S_НАБ и S_СБЕГ; dо– диаметр оси блока; f– коэффициент трения в опоре блока.

При определении значения N с некоторым допущением можно принять S_НАБ ≈ S_СБЕГ и тогда при угле обхвата блока канатом 2α

N = 2 S_НАБ sin α .

Подставив это соотношение в уравнение моментов, получим

S_СБЕГ = S_НАБ (1 + φ + 2 f sin α).

Коэффициент полезного действия блока - это отношение полезной работы S_НАБ h при подъеме груза весом G_rp на высоту h к полной работе, совершенной при этом силой S_СБЕГ на том же пути h с учетом преодоления потерь на трение и жесткости каната. Поэтому для неподвижного блока, у которого перемещение набегающей и сбегающей ветвей каната одинаково, КПД выражается формулой

η = S_НАБ / S_СБЕГ = .

Анализ этой формулы показывает, что чем больше угол обхвата блока канатом, а также чем больше жесткость каната и трение в опоре блока, тем меньше значение КПД блока и тем больше дополнительная сила, которую необходимо приложить к канату, чтобы обеспечить равномерное движение груза. На КПД блока наиболее существенное влияние оказывают потери на трение в опоре блока, зависящее от конструкции и состояния опоры, поэтому при практических расчетах с достаточной степенью точности КПД блока принимают независящим от диаметра и конструкции каната, от размеров блока и от угла обхвата его канатом.

Для блоков с опорой на подшипниках скольжения η = 0,95... 0,96; для блоков на подшипниках качения η = 0,97...0,98. Меньшие значения принимают для блоков, работающих при повышенной температуре или в запыленной или загазованной среде. Тогда натяжение ветви тягового элемента, набегающей на блок,

Sнаб = η Sсбег.

При обегании канатом неподвижного блока скорости движения набегающей и сбегающей ветви равны между собой (рис.5.23, в). Если же набегающая ветвь каната со скоростью V₁ (рис.5.23, г) набегает на подвижной блок, ось которого перемещается со скоростью V_о, то скорость сбегающей ветви каната равна

V_сбег = V₁ + 2V₀.

Основной характеристикой полиспаста является его кратность m, т.е. отношение скорости V ветви каната, набегающей на барабан, к скорости V_гр подъема груза

m = V / V_гp ,

где V = πD₂n_6ap/60; [1] стр180

D₂ - диаметр барабана, измеренный по центру сечения каната;

n_бар - частота вращения барабана, об/мин.

Частота вращения подвижного блока полиспаста определяется из следующих соображений:

Частота вращения подвижного блока должна обеспечивать скорость набегающей ветви каната V₁ и скорость перемещения оси блока V₀ , тоесть

V_окр = V₁ + V₀ ,

где V_окр = π D п / 60

V₁=V_сбег – 2V₀ – скорость набегающей ветви;

V_сбег = m V_гp,– скорость сбегающей на барабан ветви;

V₀ = V_гр – скорость груза.

Тогда

π D п / 60 = V_сбег – 2V₀+ V₀ = V_сбег – V₀ ,

Выразив V_сбег через m и V_гp и заменив V₀ на V_гp получим:

π D п / 60 = m V_гp – V_гp ,

п = , [2] стр116

где V_гp — скорость подъема, м/с;

m — кратность полиспаста;

D - диаметр блока, измеренный по центру сечения каната.

Для одинарного полиспаста кратность численно равна числу сечений канатов, на которых подвешен груз (сечение К - К на рис.5.24).

Развернутая схема обегания канатом блоков одинарного (простого) силового полиспаста приведена на рис.5.24. При отсутствии сопротивлении в полиспасте, т.е. когда система является неподвижной, сила в любой точке каната полиспаста S₀= = G_гр / m, где G_rp – вес груза; m - число сечений (ветвей) каната.

24. Схема силового полиспаста

При подъеме или опускании груза вследствие действия сил сопротивления от жесткости каната и от трения в опорах блоков натяжение отдельных ветвей каната различно. Обозначим S₁ натяжение ветви каната, идущей на обводной блок А₁; S₂ -натяжение следующей ветви и т.д. В общем случае при кратности полиспаста m натяжение последней неподвижно закрепленной ветви каната равно S_m. Отсюда

S₁ + S₂ + S₃ + … + S_m-1 + S_m = G_гр.

Соотношение между натяжениями отдельных ветвей каната при подъеме груза

S₂ = S₁η; S₃ = S₂η = S₁ η²; S₄ = S₁ η³; S_m-1 = S₁ η^m-2; S_m = S₁ η^m-1_,

где η - КПД блока.

Используя эти соотношения, получаем

G_гр = S₁ (1 + η + η² + ... + η^m-2 + η^m-1).

Вычислив сумму геометрической прогрессии (выражение в скобках), определим соотношение между весом груза G_гр и натяжением каната S₁ при параллельном расположении ветвей полиспаста без учета динамических нагрузок:

S₁ = G_гр

Натяжение S_бар каната подводимого к барабану Б, больше натяжения S₁, поскольку необходимо преодолевать сопротивление в обводных блоках A₁, A₂, A₃. Если число обводных блоков равно t, максимальное натяжение каната при подъеме груза

S_бар = S_max = = G_гр

При опускании груза максимальное натяжение S_max будет в последней ветви

S_m = G_гр

КПД полиспаста, имеющего кратность m, в целом определяется как отношение полезной работы при подъеме груза G_гр на высоту h к затраченной при этом работе S_бар m h:

η_пол = =

При этом максимальное натяжение в системе полиспаста при подъеме груза

S_max = G_гр /(m η_пол).

Подвижный блок, который следует рассматривать как полиспаст с кратностью m= 2, согласно уравнению КПД полиспаста, имеет КПД η_подв = (1 + η)/2, т.е. несколько превышающий значение КПД неподвижного блока.