1.3.2 Правильные формы кристаллов и их описание

Одно из определений кристалла гласит: «Кристаллами называются природные, искусственные или синтетические объекты, которые имеют естественную огранку, то есть их габитус (внешняя форма) является многогранником (полиэдром)». Сама форма этих многогранников может быть весьма разнообразной: на рис. 1.31 в качестве примера приведена форма монокристаллов пиропа , который, наряду с упоминавшимся ранее гроссуляром, а также с альмандином , спессартином уваровитом и андрадитом образует изоструктурную группу минералов, называемых гранатами. Поэтому габитусные полиэдры, приведенные на рис. 1.31 встречаются не только у пиропа, но и у других разновидностей группы граната. Все эти кристаллы относятся к кубической сингонии. Их ячейка – объемно-центрированная, пространственная группа Ia3d, число формульных единиц равно 8, период решетки лежит в интервале 11,4612,05 Ǻ.

Кристаллы – это атомно-молекулярные системы с регулярным вдоль любого направления расположением гомологичных (кристаллохимические тождественных) точек. Структура решетки, точнее, решеточное строение кристалла, обуславливает рентгеновскую дифракцию на этих объектах, что позволяет определять межплоскостные расстояния кристаллохимических плоскостей. Для этого необходимо определить угол  между дифракционным (рассеянным) лучом и направлением первичного луча (рис. 1.32), а затем, зная длину волны рентгеновского излучения , можно рассчитать межплоскостное расстояние dd/n (здесь n – целое число) по формуле

(1.12)

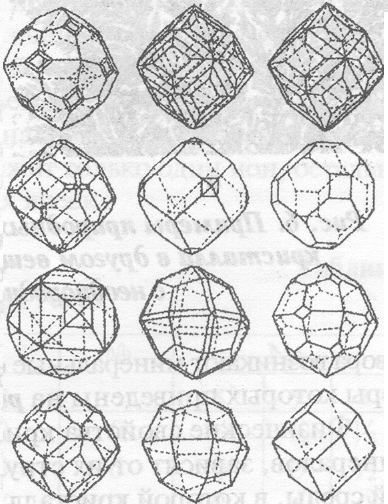
Рисунок 1.31 – Природные формы кристаллов граната

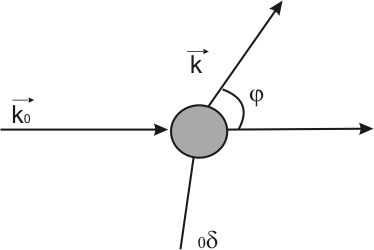
Рисунок 1.32 – Схема рассеяния рентгеновского излучения

В этой формуле угол называется бреговским, причем , а сама формула – это формула Вульфа-Брэггов (в честь Российского ученого Г.В. Вульфа и английских ученых У.Г. Брэгга и У.Л. Брэгга).

Положение плоскости в кристаллографическом барке описывается тремя целыми числами (круглые скобки обязательны), которые называются кристаллографическими индексами (обычно, просто индексами) и определяются следующим образом.

В кристалле плоскости с одинаковыми параллельны друг другу и углы ячейки вместе или по отдельности попадают на одну из этих плоскостей (в пакете), то (см. рис. 1.33) при любых одна из плоскостей этого пакета пройдет через начало координатной кристаллографической системы и через точки x=a, y=b, z=c, причем эти точки в общем случае лежат на разных плоскостях этого пакета. То есть плоскость может проходить через точку х=а, но при этом через другие точки (y=b, z=c) будет проходить не эта, а другая плоскость из плоскостей . Рассмотрим плоскость, отсекающую от координатных осей кристаллографической системы отрезки Очевидно, что где hkl – целые числа. Они то и определяют индексы плоскости. Следовательно, если заданы , то эта плоскость от координатных осей кристаллографической системы отсекает отрезки a/h, b/k, c/l, и параллельно этой плоскости проходят множество других, кристаллографически тождественных данной, причем обязательно одна из плоскостей этой совокупности пройдет через начало координат. Расстояние от начала координат до ближайшей к нему плоскости с координатами и есть межплоскостное расстояние.

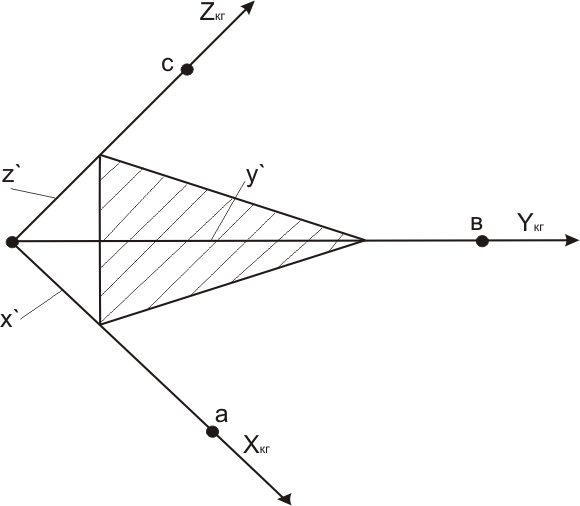
Рисунок 1.33 – К определению индексов плоскости (hkl)

Для исследования структуры кристалла, наряду с рентгеновским излучением можно использовать электронные или нейтронные пучки. Для получения электронного пучка электроны разгоняются полем с разностью потенциалов U. Схема получения картины электронной дифракции та же, что и для рентгеновских лучей (рис. 1.32).

Длина волны электронов в пучке равна

(1.13)

После подстановки в это уравнение значений постоянной Планка (h) массы и заряда электрона (me) и значения U (В) длина волны  определяется как

. (1.14)

Исследования структуры кристаллов дифракционными методами (рентгенография, электронография, нейронография) характеризуются достаточно выраженной трехэтапной схемой [41]. На первом этапе основное внимание уделяют анализу положения рентгеновских рефлексов, то есть основным экспериментальным параметром является брегговский угол . Основным уравнением первого этапа структурного анализа являются уравнение Вульфа-Брэггов (см. (1.12)), а также квадратичная формула:

(1.15)

где (a, b, c) – линейные, – угловые параметры кристалла, – кристаллографические индексы плоскости, от которой получен рефлекс.

На втором этапе решают задачу по определению структуры кристалла, то есть взаимного расположения атомов, которое описывается набором координат атомов, входящих в ячейку кристалла. Основной формулой этот этапа является

(1.16)

где – функция электронной плотности, – структурная амплитуда, определяемая интенсивности рефлекса причем

(1.17)

Так как в общем случае является комплексной величиной, то ее определение сопряжено с довольно существенными трудностями, известными под названием «фазовая проблема». Это объясняет наличие трех методов в структурном анализе: «проб и ошибок», Фурье и Паттерсона. На этом этапе структурных исследований определяют, так называемую, идеальную структурную модель, в которой приведены взаиморасположения атомов при отсутствии любых примесей и других дефектов, то есть в идеальной модели используют принцип абсолютной регулярности, соответствующий понятию бесконечно дальнего порядка.

Задачи третьего этапа связаны с определением особенностей изменений структуры в конкретном «кристаллическом индивидууме» в зависимости от его состава, дефектности, внешних воздействий (термическая обработка, деформирование, облучение, действие полей и т. д.). Основного, единого метода для решения этих задач нет, но известно, что необходимая информация может быть получена не только из анализа положений и интенсивностей рассеяния (модуляции фона).

Кристаллические образцы, предназначенные для структурных исследований, могут быть монокристаллами (это основное требование для второго этапа) или поликристаллами (первый и третий этапы). При исследовании поликристаллов, когда размеры кристаллов достаточно маленькие, наблюдается усиление рентгеновских рефлексов. Следовательно, размеры частиц в порошке можно определить рентгеновскими методами. Расчет L осуществляют по формуле Шеррера

(1.18)

где – длина волны рентгеновского излучения, – брэгговский угол, определяемый по максимальной интенсивности рефлекса, – угловая полуширина рефлекса, т. е. угловая ширина на половине высоты рефлекса.

Как видно из рис. 1.31, формы кристаллов одного и того же вещества могут быть достаточно различными. Однако, каждая из плоских граней может быть описана индексами параллельной этой грани кристаллографической плоскости. Если кристалл ограничен только плоскостями, связанными между собой группой точечной линии (С), то полиэдр, ограненный этими плоскостями, называется правильной формой кристалла. Следовательно, для получения индексов граней правильных форм кристаллов – ( ) – необходимо использовать формулу , где и – матрицы-столбцы индексов граней правильной формы и исходной грани соответственно.

Если один или два индекса исходной грани равны нулю, или взаиморавны два или три индекса, полученная форма является частной. Индексы граней общих и частных простых форм кристаллов различных точечных групп, а также названия габитусных полиэдров приведены в табл. 1.2-1.5. Число граней простой формы равно фактору повторяемости при поликристаллических рентгенодифракционных исследованиях. При записи индексов граней правильных форм использованы следующие сокращения. Если порядок индексов не меняется, то над ними или перед ними указаны лишь их знаки. Например, группа 2/m имеет форму , , , и в краткой форме записывается в виде или . Запись означает плоскости с циклической перестановкой индексов, т.е. . Запись означает перестановку индексов Если необходимо осуществить перестановку знаков, над индексами ставится символ S. Например, группа 4mm имеет форму что тождественно записи .

Таблица 1.2