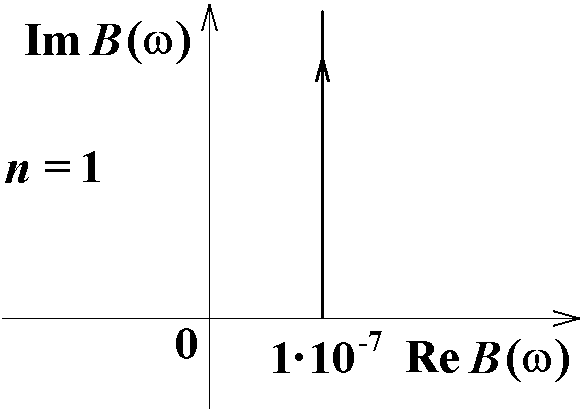Методические указания к решению задач 41–50

Исследуем приведенную на рис. 12 схему на устойчивость с помощью критериев Гурвица и Михайлова.

Устойчивыми называются системы (цепи), в которых токи и напряжения после снятия внешнего воздействия с течением времени уменьшаются до нуля (затухают).

Неустойчивыми называют системы (цепи), в которых токи и напряжения по окончании действия внешнего возмущения продолжают возрастать. В реальных цепях неустойчивость вызывает самовозбуждение, т.е. генерацию нежелательных колебаний.

Анализ и расчет схем на устойчивость занимают в теории и практике применения электронных цепей очень важное место. Одна из глобальных целей расчета схем − обеспечить устойчивую работу соответствующих цепей в реальных условиях эксплуатации. Невыполнение указанной цели характеризует некачественность проведенных расчетов.

Анализ схемы на устойчивость проводят различными способами, основанными на анализе знаменателя схемной функции и отличающимися характером критерия. Среди них алгебраический критерий устойчивости Гурвица, частотный критерий устойчивости Михайлова, позволяющий судить об устойчивости по виду частотного годографа, и др.

Анализ схемы на устойчивость по критерию Гурвица.

Это алгебраический критерий, который предполагает рассмотрение знаменателя схемной функции B(p), записанного в виде многочлена степени n:

(19)

Из его коэффициентов b_i по следующему правилу составляется матрица Гурвица: на главной диагонали сверху вниз выписываются по порядку коэффициенты от b₁ до b_n включительно. В каждом строке вправо от диагонали записывают коэффициенты при убывающих степенях оператора p, влево – при возрастающих степенях p. Недостающие элементы в столбцах заменяются нулями. Размерность матрицы Гурвица – n  n.

Критерий устойчивости Гурвица формулируется следующим образом: для устойчивости системы необходимо и достаточно, чтобы все n определителей, получаемых из матрицы Гурвица H, были положительны.

Здесь

…

Исследуем на устойчивость с помощью данного критерия нашу схему (рис. 12). Из рассмотренного выше примера известно, что ее схемная функция (в данном случае коэффициент передачи по напряжению) имеет вид

Исследуем знаменатель схемной функции B(p) = pCg₃ + g₂g₃. Очевидно, что b₁ = Cg₃ , а b₀ = g₂g₃. Схема устойчива, если

Поскольку C (емкость) и g₃ (проводимость резистора R₃) всегда положительны, для схемы на рис. 12 критерий Гурвица выполняется при любых значениях параметров C и g₃, т.е. данная схема всегда устойчива.

Анализ схемы на устойчивость по критерию Михайлова.

Для анализа устойчивости рассматривается знаменатель схемной функции B(jω), который получается из полинома (19) заменой p на jω:

(20)

где можно выделить вещественную и мнимую часть, а также амплитуду и фазу:

Для конкретного численного значения ω = ω_i имеем комплексное число B(jω_i), которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой (Re B(ω_i); j Im B(ω_i)). При изменении ω от 0 до ∞ конец вектора B(jω) выписывает на комплексной плоскости некоторую кривую, которую называют годографом Михайлова. При этом годограф начинается, как следует из выражения (20), в точке с координатами (b₀; j0).

Критерий устойчивости Гурвица формулируется следующим образом: для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении ω от 0 до ∞ начинался на положительном конце вещественной оси в точке b₀ и проходил последовательно против часовой стрелки n квадрантов, не обращаясь в ноль и стремясь к ∞ в n-ом квадранте.

В устойчивой системе каждый из n корней даст приращение фазы φ_i = + π/2, а общий угол поворота B(jω) равен + (π/2)n. Вид годографа Михайлова для устойчивой и неустойчивых схем третьего порядка (т.е. у которых знаменатель схемной функции B(p) является полином 3-ей степени) приведен на рис. 15.

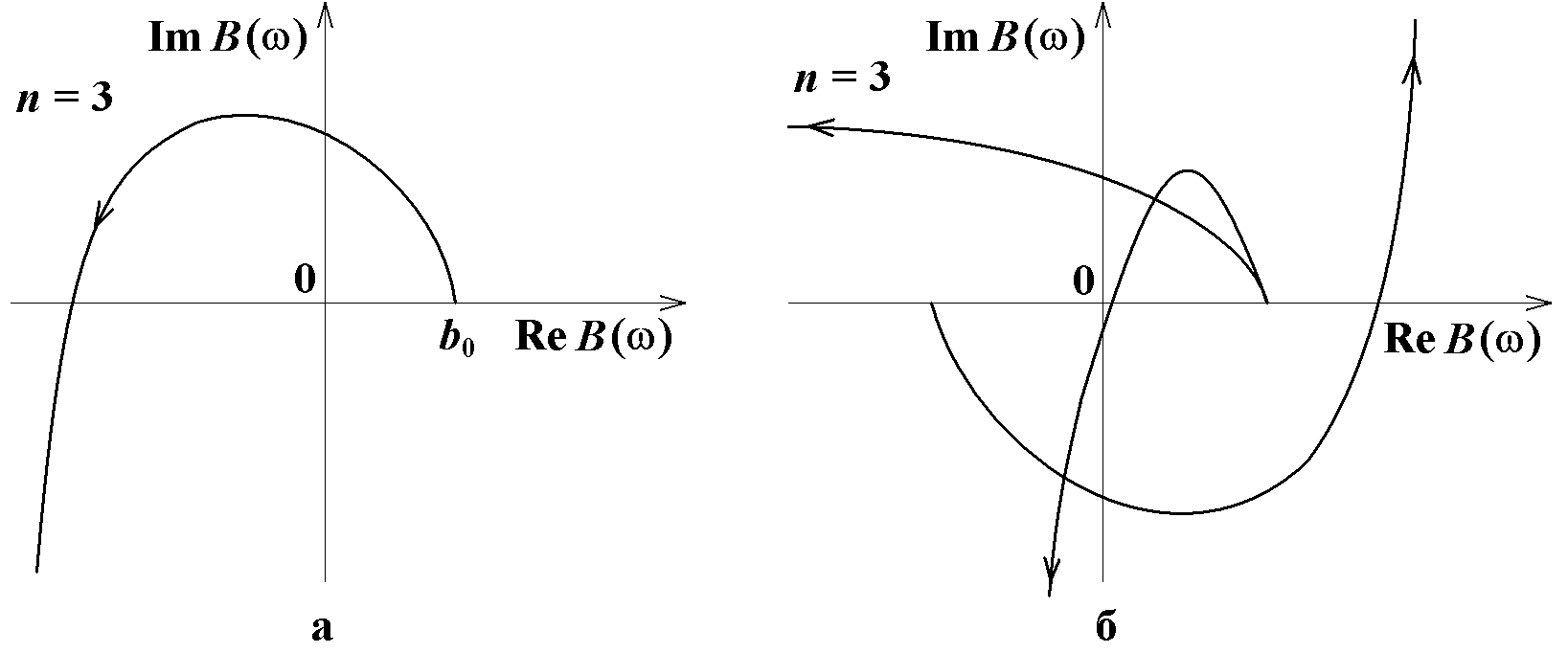
Рис. 15. Примеры годографа Михайлова для устойчивой (а) и неустойчивых (б) систем третьего порядка (n = 3)

Оценим устойчивость схемы на рис. 12 по критерию Михайлова. Полином знаменателя схемной функции имеет вид

B(p) = pCg₃ + g₂g₃.

Заменив p на jω, получим выражение для годографа Михайлова

B(jω) = jωCg₃ + g₂g₃,

в котором Re B(ω) = g₂g₃ = 1·10^-7 См²; Im B(ω) = ωCg₃ = 1·10^-10 Ф·См.

Для построения годографа Михайлова вычислим значения вещественной и мнимой частей при конкретных значениях частоты и занесем их в таблицу.

Таблица. Координаты точек для построения годографа Михайлова

ω	0	1	10	100	∞
Re B(ω)	1·10-7	1·10-7	1·10-7	1·10-7	1·10-7
Im B(ω)	0	1·10-10	1·10-9	1·10-8	∞

Вид годографа Михайлова для схемы на рис. 12 представлен на рис. 16.

Рис. 16. Годограф Михайлова для схемы на рис. 12

Поскольку годограф начинается на положительном конце реальной оси, попадает в первый квадрант и стремится к ∞ в первом квадранте (у нас n = 1), схема является устойчивой. Данный вывод совпадает с результатами анализа схемы по критерию устойчивости Гурвица.