
- •И.М.Баранова, н.А.Часова, г.Д. Алексеева, а.Н.Муравьев
- •Математика
- •Брянск 2006
- •Пусть имеется выборка результатов испытаний
- •1. Показатели центра распределения
- •2. Показатели рассеяния
- •3. Показатели формы распределения
- •Напомним, что мода – точка максимума дифференциальной функции распределения.
- •6. Точечные и интервальные оценки параметров генеральной совокупности
- •7. Статистическая проверка гипотез
- •8. Предварительный выбор закона распределения
- •Проверка гипотезы о виде распределения
- •Приложение 2
- •ЛИтература
- •241037, Г. Брянск, пр. Станке Димитрова, 3, редакционно–издательский
3. Показатели формы распределения
На практике
приходится встречаться с самыми
различными распределениями. Однородные
совокупности характеризуются, как
правило, одновершинным распределением.
Многовершинность свидетельствует о
неоднородности изучаемой совокупности.
При изучении распределений, отличных
от нормального, возникает необходимость
количественно оценить это различие. С
этой целью вводят такие характеристики,
как коэффициент асимметрии
![]() и коэффициент эксцесса ε.
Для нормального распределения эти
характеристики равны нулю. Поэтому,
если для изучаемого распределения
асимметрия и эксцесс имеют небольшие
значения
и коэффициент эксцесса ε.
Для нормального распределения эти
характеристики равны нулю. Поэтому,
если для изучаемого распределения
асимметрия и эксцесс имеют небольшие
значения
![]() ;
;
![]() ,
то можно предположить близость этого
распределения к нормальному.
,
то можно предположить близость этого
распределения к нормальному.
Коэффициент асимметрии определяется по формуле:
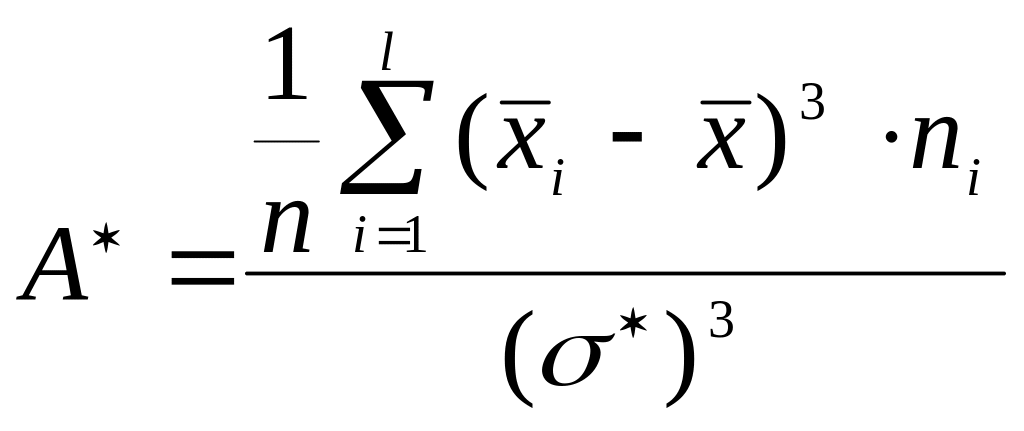 .
.
Если
![]() =0,
то ряд симметричен относительно моды.
=0,
то ряд симметричен относительно моды.
При
>0
скошенность вправо, средняя арифметическая
правее моды, «длинная часть» кривой
распределения расположена справа от
моды. При правосторонней асимметрии
![]() .
.
При
<0
скошенность вправо, средняя арифметическая
левее моды, «длинная часть» кривой
распределения расположена слева от
моды. При левосторонней асимметрии
![]() .
.
Напомним, что мода – точка максимума дифференциальной функции распределения.
В нашем случае:
![]() .
.
К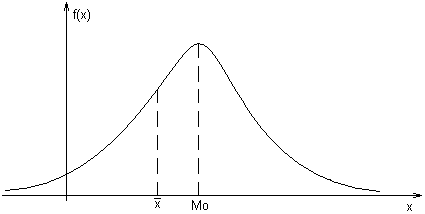 оэффициент
асимметрии отрицательный, следовательно
“длинная часть” кривой, полученной на
основании опытных данных, расположена
слева от моды и средняя арифметическая
левее моды (рисунок 3). Заметим, что в
нашем случае коэффициент асимметрии
близок к нулю.
оэффициент
асимметрии отрицательный, следовательно
“длинная часть” кривой, полученной на
основании опытных данных, расположена
слева от моды и средняя арифметическая
левее моды (рисунок 3). Заметим, что в
нашем случае коэффициент асимметрии
близок к нулю.
Рисунок 3. Левосторонняя асимметрия.
![]()
Коэффициент эксцесса определяется по формуле:
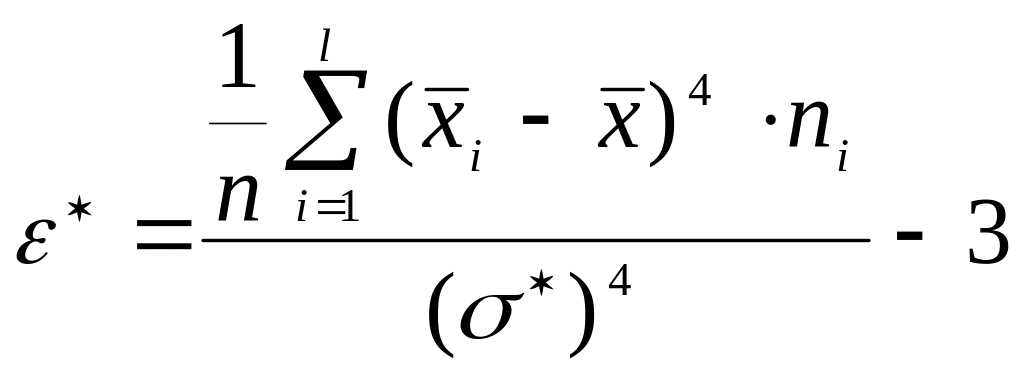
Если ε*>0, то кривая имеет более высокую и острую вершину, чем нормальная кривая (островершинное распределение); если ε*<0, то сравниваемая кривая имеет более низкую и "плоскую" вершину, чем нормальная кривая (плосковершинное распределение).
Замечание:
–2 < ε*<
![]() .
Если ε*
близок к –2, то кривая двухвершинная.
При ε
=
–2 кривая распадается на 2 островершинные
кривые, что говорит о неоднородности
статистического материала.
.
Если ε*
близок к –2, то кривая двухвершинная.
При ε
=
–2 кривая распадается на 2 островершинные
кривые, что говорит о неоднородности
статистического материала.
В нашем случае:
![]() .
.
К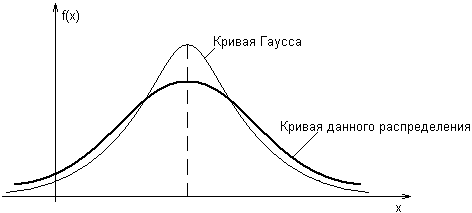 оэффициент
эксцесса отрицательный, следовательно,
вершина кривой ряда распределения ниже,
чем у кривой нормального распределения.
оэффициент
эксцесса отрицательный, следовательно,
вершина кривой ряда распределения ниже,
чем у кривой нормального распределения.
Рисунок 4. – Плосковершинное распределение.
6. Точечные и интервальные оценки параметров генеральной совокупности
Задачи математической статистики практически сводятся к оценке свойств генеральной совокупности по результатам случайной выборки.
Любую
функцию
![]() от результатов выборочных наблюдений
от результатов выборочных наблюдений
![]() принято
называть статистикой (выборочной
характеристикой). Статистики обычно и
используются для построения статистических
оценок параметров
принято
называть статистикой (выборочной
характеристикой). Статистики обычно и
используются для построения статистических
оценок параметров
![]() генеральной совокупности, когда точные
значения этих параметров нам неизвестны.
Статистику
генеральной совокупности, когда точные
значения этих параметров нам неизвестны.
Статистику
![]() ,
используемую как оценку параметра
,
называют точечной оценкой. Из точечных
оценок в приложениях математической
статистики наиболее часто используют
среднюю арифметическую
,
используемую как оценку параметра
,
называют точечной оценкой. Из точечных
оценок в приложениях математической
статистики наиболее часто используют
среднюю арифметическую
![]() как оценку математического ожидания
М(х)=а,
выборочную дисперсию D*
и среднее квадратическое отклонение
как оценку математического ожидания
М(х)=а,
выборочную дисперсию D*
и среднее квадратическое отклонение
![]() ,
как оценки генеральной дисперсии D(x)
и среднего квадратического отклонения
,
как оценки генеральной дисперсии D(x)
и среднего квадратического отклонения
![]() .
.
В математической статистике в зависимости от задачи статистику рассматривают либо как СВ, либо как число (конкретную реализацию СВ). Возникает вопрос, каким требованиям должны отвечать точечные оценки, чтобы их можно было считать в каком–то определенном смысле "хорошими". Эти требования характеризуют понятиями несмещенности, состоятельности и эффективности.
Оценку
![]() называют несмещенной, если при любом
объеме выборки n
ее математическое ожидание равно
оцениваемому параметру
,
то есть М(
называют несмещенной, если при любом
объеме выборки n
ее математическое ожидание равно
оцениваемому параметру
,
то есть М(![]() )
=
.
В случае большой выборки оценка
)
=
.
В случае большой выборки оценка
![]() параметра
называется состоятельной, если по мере
роста числа наблюдений n
(то есть
параметра
называется состоятельной, если по мере
роста числа наблюдений n
(то есть
![]() в случае конечной генеральной совокупности
объемом N
или при
в случае конечной генеральной совокупности
объемом N
или при
![]() в случае бесконечной генеральной
совокупности) она стремится к оцениваемому
параметру
.
в случае бесконечной генеральной
совокупности) она стремится к оцениваемому
параметру
.
Несмещенная оценка параметра называется эффективной, если среди прочих несмещенных оценок того же параметра она обладает наименьшей дисперсией.
Точечные оценки параметров генеральной совокупности в нашем примере:
![]()
Точечная оценка без указания степени точности и надежности малоинформативна, так как наблюдаемые значения статистики есть лишь значения СВ. Она может существенно отличаться от оцениваемого параметра при малом объеме выборки, что приводит к грубым ошибкам.
Интервальной
оценкой параметра
называют такой интервал
![]() ,
относительно которого можно утверждать
с определенной, близкой к единице
вероятностью
,
относительно которого можно утверждать
с определенной, близкой к единице
вероятностью
![]() ,
что он содержит неизвестное значение
.
Величину
называют доверительной вероятностью
или надежностью оценки параметра Θ:
,
что он содержит неизвестное значение
.
Величину
называют доверительной вероятностью
или надежностью оценки параметра Θ:
![]() ,
,
![]() –
некоторые функции от результатов
выборочных наблюдений
–
некоторые функции от результатов
выборочных наблюдений
![]() .
Разность 2
.
Разность 2![]() =
–
между
верхней и нижней границами доверительного
интервала называют длиной доверительного
интервала, а величину
– точностью оценки.
=
–
между
верхней и нижней границами доверительного
интервала называют длиной доверительного
интервала, а величину
– точностью оценки.
Для
построения интервальных оценок необходимо
знать закон распределения статистики
![]() .
.
На практике закон распределения генеральной совокупности неизвестен. В этом случае пользуются приближенным методом построения доверительных интервалов, суть которого в следующем: если считать, что распределение выборочных характеристик в больших выборках асимптотически нормальное (для дисперсии это справедливо при n >100, а для средней арифметической при n > 30), то доверительные интервалы строятся следующим образом
![]()
где
– оцениваемый параметр;
*
– выборочная оценка параметра;
![]() –
число, определяемое из равенства
–
число, определяемое из равенства
![]() .
.
По таблице значений функции Лапласа
![]()
находят
аргумент
![]() ,
которому соответствует значение функции
Лапласа, равное
,
которому соответствует значение функции
Лапласа, равное
![]() .
.![]() При
При
![]() .
.
![]() – стандартные
ошибки выборочной характеристики
(главный член среднего квадратического
отклонения).
– стандартные
ошибки выборочной характеристики
(главный член среднего квадратического
отклонения).
Стандартные ошибки:
1) Выборочной
средней
![]() .
В нашем примере
.
В нашем примере
![]()
2) Выборочной
дисперсии
![]()
В примере
![]()
3) Выборочного
среднеквадратического отклонения
![]() :
:
![]() .
.
В примере
![]()
4) Выборочного
коэффициента асимметрии
![]() :
:
![]()
5) Выборочного
коэффициента эксцесса
![]()
6) Выборочного
коэффициента вариации
![]() :
:

7) Выборочной
медианы
![]()
![]()
Построим доверительные
интервалы для параметров генеральной
совокупности нашего примера при
![]() .
.
Для математического ожидания:
![]()
![]()
![]() .
.
Для дисперсии:
![]()
![]()
![]() .
.
Для среднеквадратического отклонения:
![]()
![]()
![]() .
.
Для коэффициента асимметрии:
![]()
![]()
![]() .
.
Для коэффициента эксцесса:
![]()
![]()
![]() .
.
Для коэффициента вариации:
![]()
![]()
![]() .
.
Для медианы:
![]()
![]()
![]() .
.
