1. Показатели центра распределения

Для характеристики центра распределения в вариационном ряду используются:

1. Средняя арифметическая, которая определяется по формуле:

где – значение признака для дискретного ряда или середина интервала для интервального статистического ряда.

В нашем случае: .

2. Мода – наиболее часто встречающееся значение признака. Для дискретного ряда мода – значение признака, соответствующего наибольшей частоте. Для интервального ряда мода вычисляется по следующей приближенной формуле:

,

где – нижняя граница модального интервала, то есть интервала, имеющего наибольшую частоту;

– длина интервала;

– частота модального интервала;

– частота интервала, предшествующего модальному;

– частота интервала, следующего за модальным.

В примере модальным является 6 интервал.

Мода может быть определена приближенно графическим способом. Для этого правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых приближенно будет модой распределения. В рассматриваемом примере = 4.11 (рисунок 1).

3. Медиана – значение признака, которое делит весь упорядоченный ряд значений пополам. Для дискретного ряда, если число вариант нечетно, т. е. n = 2k+l, Me = 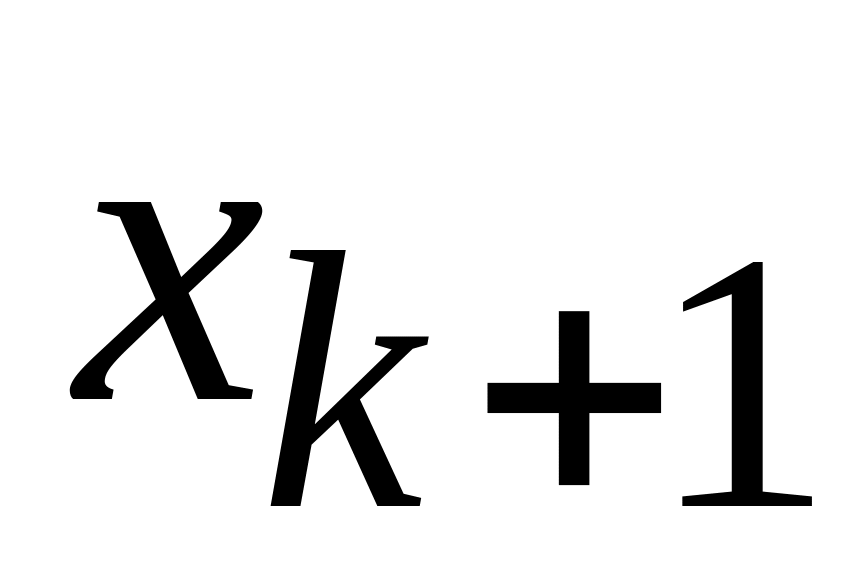, при четном n = 2k Me =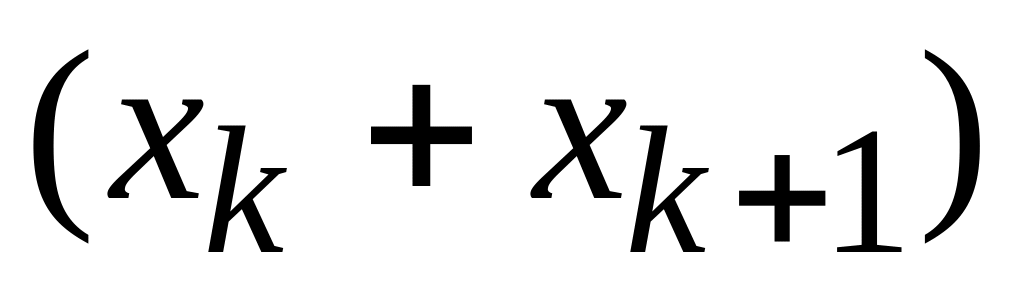 /2. Для интервального статистического ряда медиана вычисляется по следующей приближенной формуле:

где – нижняя граница медианного интервала, то есть интервала, которому соответствует первая из накопленных частот, превышающая половину объема совокупности; – длина интервала; – частота медианного интервала; – накопленная частота интервала, предшествующего медианному.

В примере медианным является 3-й интервал.

.

По кумуляте (рисунок 2) приближённо определим значение медианы: на уровне 0.5 (накопленная относительная частота) проведем горизонтальную линию до пересечения с кумулятой; в точке пересечения опустим перпендикуляр на ось абсцисс; точка, в которой перпендикуляр пересекает ось абсцисс, показывает приближенное значение медианы. В нашем примере .

2. Показатели рассеяния

Для характеристики отклонения значений признака от среднего арифметического используются:

1. Дисперсия, которая определяется по формуле:

В нашем случае: .

2. Среднее квадратическое отклонение

В нашем случае: .

3. В качестве относительной характеристики рассеяния используют коэффициент вариации, который показывает, насколько велико рассеяние значений признака по сравнению со средней арифметической. Коэффициент вариации определяется по формуле:

В отличие от дисперсии и среднего квадратического отклонения коэффициент вариации – величина безразмерная, что позволяет сравнивать изменчивость признаков как в пределах одной совокупности, так и разных совокупностей, независимо от единиц измерения разных сопоставляемых признаков.

Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).

Исходя из величины коэффициента вариации, можно установить характеристику изменчивости, например, по следующей схеме:

Коэффициент вариации,	До 5%	6–10%	11–20%	21–50%	50%
Изменчивость	слабая	умеренная	значительная	большая	очень большая

В нашем случае: , следовательно, изменчивость умеренная, совокупность однородна.