4.3. Вывод и анализ формулы Планка

Задача о продолжительности замораживания – одна из наиболее сложных в теплофизике замораживания, что обусловлено наличием большого числа влияющих на этот процесс факторов.

Каждый из существующих на сегодняшний день методов вычисления продолжительности замораживания специфически связан с исходной физической схемой процесса, его начальными и граничными условиям, которые задаются в частном виде, с допущениями, упрощающими задачу.

Физическая постановка задачи о продолжительности замораживания пищевых продуктов есть задача о теплопроводности в системах с подвижной границей раздела, под которой понимают перемещающуюся границу раздела между отвердевшей и жидкой фазами от периферии в глубь тела по мере отвода теплоты от его поверхности. Отвердевающую в таком процессе жидкость принято рассматривать как не подверженную свободному или вынужденному конвективному движению, если она распределена в виде мелких включений в пористом твердом теле или как-либо иначе, механически связана с неподвижной скелетной структурой тела, а также, если вязкость отвердевающей жидкости велика.

Классическим решением задачи о замораживании Международным институтом признано решение Р. Планка, полученное им в 1913 г. и существенно развитое им и другими исследователями в последующие годы. Формула для определения продолжительности замораживания называется по имени ее создателя – формула Планка, как фундаментальная, она включена в рекомендации Международного института холода.

Для упрощения задачи Планком было сделано несколько допущений, которые приведены ниже:

1. Теплоемкость замороженной части продукта равна нулю.

2. Тело перед началом замораживания охлаждено до криоскопической температуры.

3. Льдообразование в теле происходит без переохлаждения при криоскопической температуре; теплофизические свойства замороженной части (коэффициент теплопроводности и удельная теплоемкость) не зависят от температуры.

4. Тело однородно, его плотность при замораживании не меняется; коэффициент теплоотдачи и температура охлаждающей среды не зависят от времени.

Выведем формулу Планка для тела в форме пластины. Пусть за некоторый промежуток времени тело замерзло на толщину (рис. 9). При этом выделилось тепло в количестве в результате превращения воды в лед. Тогда за промежуток времени , тело промерзнет на толщину , при этом выделится тепло в количестве .

x,

dx, d

F, =const, t₀=const

C_мор.=0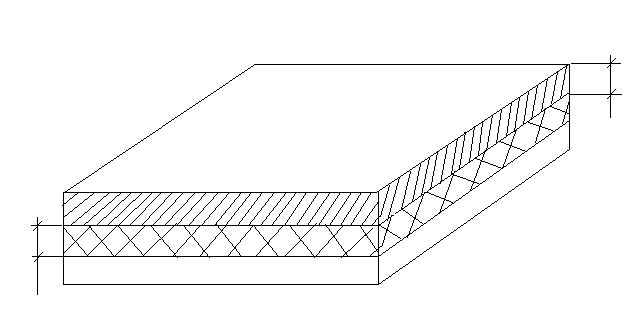

Рисунок 9 – Вывод формулы Планка для тела в форме пластины

, (63)

где - масса замороженного продукта, кг.

- теплота, выделенная при замораживании единицы массы продукта, кДж/кг, рассчитывается по формуле

, (64)

где - содержание воды в продукте, доли единицы;

- количество вымороженной воды, доли единицы;

- скрытая теплота льдообразования, кДж/кг.

Тогда, подставив выражение (64) в формулу (63) получим

. (65)

Если учесть, что масса продукта есть произведение его плотности на объем, то приращение массы замороженного продукта составит

, (66)

где - приращение замороженного объема продукта, м³.

Для пластины, площадь которой , м², а толщина , приращение объема составит

. (67)

Подставив выражения (67) и (66) в формулу (65) получим

. (68)

В силу третьего допущения Планка (теплоемкость замороженной части продукта равна 0, что превращает коэффициент температуропроводности этой части продукта в бесконечность), вся теплота, которая выделилась в результате льдообрзования, будет передана через замороженный слой продукта к поверхности замораживаемого тела и должна быть отведена от нее охлаждающей средой .

Для отдностороннего замораживания тела через плоскую стенку (замороженный слой продукта) это количество теплоты может быть выражено уравнением теплопередачи через плоскую стенку

, (69)

где - коэффициент теплопередачи, может быть рассчитан по формуле

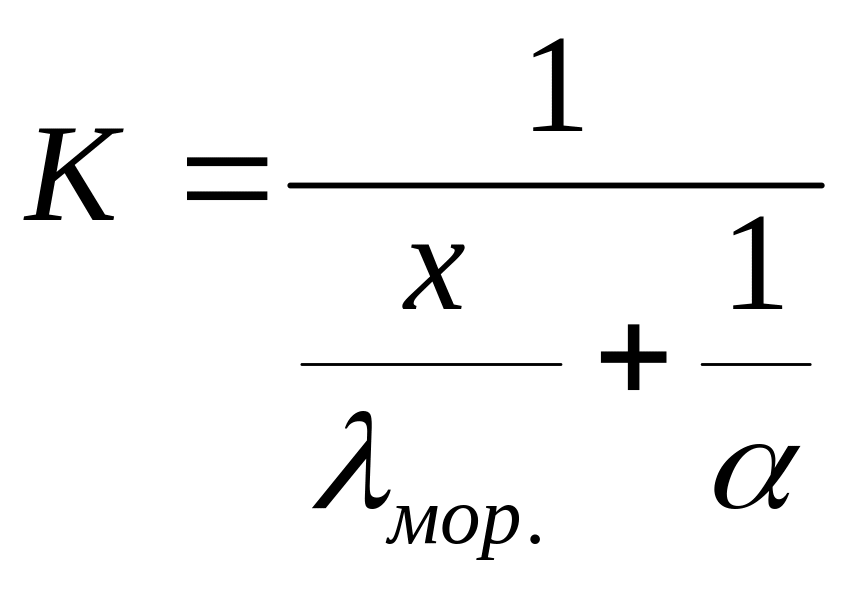, (70)

где - коэффициент теплопроводности мороженого продукта, Вт/(м·К);

- коэффициент теплоотдачи, Вт/(м²·К);

- толщина стенки (толщина замороженного слоя продукта), м.

Так как

, (71)

то

, (72)

после преобразований, выразим из уравнения (72) , получим

. (73)

Уравнение (73) после интегрирования дает выражение для определения продолжительности замораживания тела в форме пластины – формулу Планка для пластины

. (74)

Очевидно, что при несоблюдении допущенных Планком упрощений, значительно усложнились бы условия интегрирования дифференциального уравнения (73).

В формуле (74) в случае одностороннего замораживания, - это полная толщина пластины, а в случае двустороннего замораживания - это половина толщины пластины.

Для тел в форме шара и цилиндра формула Планка получена аналогичным путем, имеет вид

- для цилиндра

, (75)

- для шара

, (76)

где - радиус шара, цилиндра, м.

Сравнив формулы (74), (75) и (76) можно сделать вывод, что минимальной продолжительность замораживания будет для тела в форме шара, а максимальной – для тела в форме пластины.

В силу сделанных Планком допущений, расчетные продолжительности замораживания будут отличаться от реальных примерно на 10-15 %, что вполне допустимо в инженерных расчетах.

Анализ формулы Планка позволяет выявить основные факторы, оказывающие влияние на продолжительность процесса замораживания, к ним относятся:

- коэффициент теплоотдачи охлаждающей среды, чем он больше, тем меньше продолжительность процесса замораживание и выше его скорость;

- температура охлаждающей среды, чем ниже температура охлаждающей среды, тем меньше продолжительность процесса и выше скорость замораживания;

- толщина продукта, причем зависимость носит квадратичный характер, то есть при увеличении толщины продукта, например, в 2 раза, продолжительность процесса возрастет в 4 раза.