2.2 Арифметические операции над двоичными числами.

Арифметические операции над двоичными числами могут производиться по тем же правилам, что и над десятичными, однако, с целью упрощения цифровых систем для выполнения арифметических операций применяют алгоритмы, отличные от алгоритмов действий десятичной арифметики.

В двоичной системе счисления для представления знака числа используется дополнительный знаковый разряд (один или несколько разрядов), который располагается перед старшим числовым разрядом. Для положительных чисел значение знакового разряда Зн.р.=0, для отрицательного числа Зн.р.=1.

Операция вычитания в цифровых системах реализуется с помощью операции сложения.

Вычитаемое при этом представляется в дополнительном коде (если расчет не требует высокой точности - в обратном коде).

Двоичный код со знаком называют также прямым кодом. В качестве примера

рассмотрим положительное и отрицательное числа, десятичный эквивалент которых равен 46₁₀.

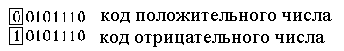
  Обратный код получается путем замены всех “0” на “1” и всех “1” на “0” прямого кода (двоичного числа со знаком). Причем, знаковый разряд при этом остается неизменным.

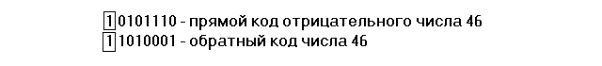
Замена “0” на единицу (“1”) называется инвертированием (также и замена “1”на “0”).

Обратный код, дополненный единицей в младшем разряде, называется дополнительным кодом. Последовательность действий при получении дополнительного кода:

 

Сложение и вычитание двоичных чисел. Правила сложения двух двоичных чисел можно показать на следующем примере:

Пример сложения многоразрядных чисел. Требуется сложить два числа 18₁₀ и 23₁₀

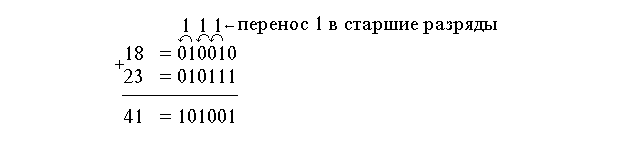
Вычитание в цифровых устройствах производится также как и сложение, только вычитающее представляется в дополнительном коде. Рассмотрим два примера, в первом требуется из числа 23 отнять число 18, а во втором из 18 отнять 23. С начала вычитающие представим в дополнительном коде:

010010 – 18 прямой код

101101 – 18 обратный код

+

1

________

101110 – 18 дополнительный код

010111 – 23 прямой код

101000 – 23 обратный код

+

1

________

101001- 23 дополнительный код

1)

Таким образом, получилось число плюс 5.

2)

Таким образом, получилось число минус 5.

Принято считать, что дополнительный код положительного числа совпадает с его прямым кодом. Операция вычитания с использованием только обратного кода (без дополнительных операций по переводу его в дополнительный код) приводит к ошибке, определяемой единицей в младшем разряде, и поэтому при точных расчетах не применяется.

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.

Пример. 1001 101=?

    

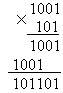
Результат 1001 101=101101.

Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.

Пример. 1100.011 : 10.01=?

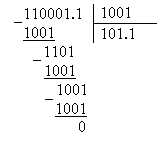
Результат 1100.011 : 10.01=101.1.