2.3. Граф досяжності

В основі дослідження перерахованих у п.2.2. властивостей мереж Петрі лежить аналіз досяжності.

Один з методів аналізу досяжності будь-якого маркування з стану М₀ — побудова графа досяжності. Початкова вершина графа відображає М₀, а решта вершин відповідають маркуванням. Дуга з М_i в М_j означає подію M_i  M_j і відповідає спрацюванню перехода t.

У складних мережах граф може містити надзвичайно велику кількість вершин і дуг. Проте при побудові графа можна не відображати всі вершини, оскільки багато з них є дублями (дійсно, від маркування M_k завжди породжується один і той самий підграф не залежно від того з якого стану система прйишла в М_k). Тупики виявляються за відсутністю дозволених переходів з будь-якої вершини, тобто за присутністю листків — термінальних вершин. Необмежене зростання кількості маркерів в будь-якій позиції свідчить про порушення обмеженості.

Приклад 2.1. Часткове дерево досяжності маркованої мережі Петрі. Мережа Петрі має вигляд:

Р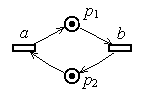 ис.2.2 Приклад мережі Петрі

Часткове дерево досяжності для трьох кроків побудови має вигляд:

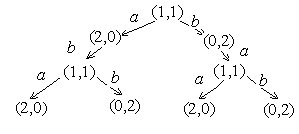
Рис.2.3. Часткове дерево досяжності мережі Петрі для прикладу 2.1.

Для мережі Петрі з безмежною множиною досяжних маркувань дерево досяжності є безмежним. Мережа Петрі з скінченою множиною досяжних маркувань також може мати безмежне дерево досяжності (див. приклад 2.1). Для перетворення безмежного дерева в корисний інструмент аналізу будується його скінчене представлення. При побудові скінченого дерева досяжності для позначення безмежності множини значень маркування позиції використовується символ .

Приклад 2.2. Мережа Петрі і її граф досяжних роміток представлені на рис.2.4.

На рисунку вершини графа зображені у вигляді маркувань, дуги помічені спрацьовуючими переходами. Активність мережі є очевидною, оскільки спрацьовують всі переходи, тупики відсутні.

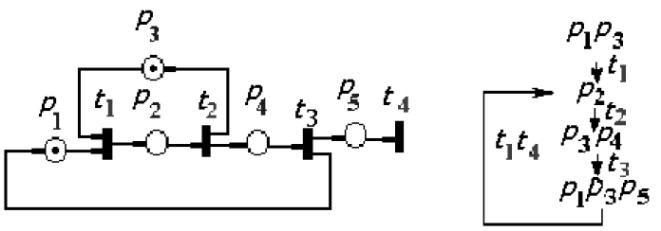
Рис.2.4.Мережа Петрі і її граф досяжності для прикладу 2.2.

Приклад 2.3. Мережа Петрі і її граф досяжних роміток представлені на рис.2.5.

Мережа моделює двохпроцесорну обчислювальну систему з загальною пам’яттю, є живою, всі розмітки досяжні.

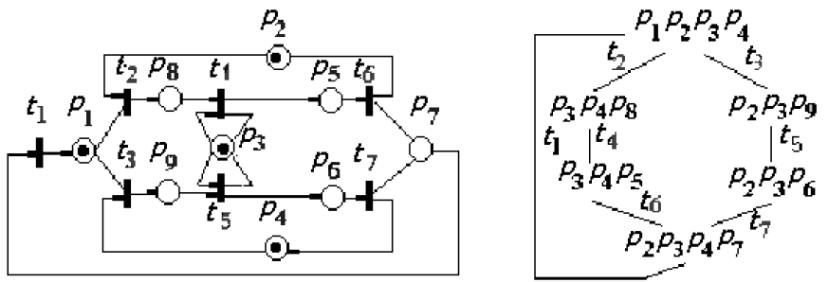
Рис.2.5.Мережа Петрі і її граф досяжності для прикладу 2.3.

Приклад 2.4. Наступна мережа (рис. 2.6,а.) визначає керування двома паралельно протікаючими процесами з синхронізацією. Граф досяжності показано на рис. 2.6,б. Граф розгортки мережі є безмежним (рис 2.6,б), проте після стану М3 у кожній гілці повторюється один і той самий фрагмент і тому можливе скінчене представлення графа досяжності (рис.2.6,в).

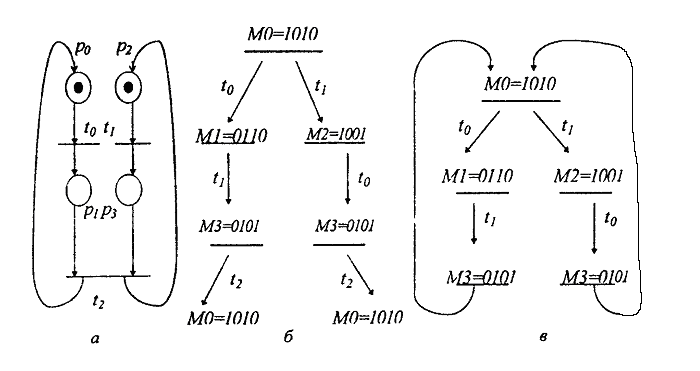
Рис.2.6. Мережа Петрі і її граф досяжності для прикладу 2.3.

Алгоритм побудови сконченого дерева досяжності. Кожна вершина дерева досяжності класифікується алгоритмом або як гранична вершина, термінальна вершина, дублююча вершина, або як внутрішня вершина. Алгоритм починає роботу із визначення початкового маркування коренем дерева, і граничною вершиною. Один крок алгоритму полягає в обробці граничної вершини. Нехай х — гранична вершина, тоді її обробка полягає у наступному:

1. Якщо в дереві є інша вершина y, яка не є граничною, і з нею пов’язана те саме маркування, М[x]=М[y], тоді вершина х стає дублюючою.

2. Якщо для маркування М[х] жоден з переходів не дозволений, тоді x стає термінальною.

3. У іншому випадку, для будь-якого переходу tT, дозволеного в М[х], створюється нова вершина z дерева досяжності. Маркування М[z], яке пов’язане з цією вершиною, визначається для кождої позиції pP наступним чином:

3.1. Якщо М[х](p)=, тоді М[z](p)=.

3.2. Якщо на шляху від кореневої вершини до x існує вершина y з М[y]<М’ (де М’ – маркування, дезпосередньо досяжна з Мх] шляхом запуску перехода t) і М[y](p)<М’(p), тоді М[z](p)=. (У цьому випадку послідовність запусків переходів, яка веде з маркування М[y] у маркування М’, може необмежено повторюватися і необмежено збільшувати значення маркування в позиції p.) В іншому вмпадку М[z](p)=М’(p).

4. Будується дуга з поміткою t, яка направлена від вершини x до вершини z. Вершина х стає внутрішньою, а вершина z – граничною.

Така обробка алгоритмом граничних вершин продовжується доти, поки всі вершини дерева не стануть термінальними, дублюючими або внутрішніми. Потім алгоритм зупиняється.

Зауваження. Важливою властивістю алгоритму побудови сконченого дерева досяжності є те, що він за скончену кількість кроків завершує роботу.

Пример 2.5. Скінчене дерево досяжності мережі Петрі.

Р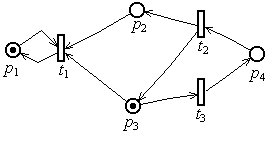 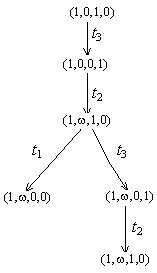ис.2.7. Мережа Петрі та скінчене дерево досяжності для прикладу 2.5.