1.5 Красно-черные деревья

Красно-чёрное дерево (red-black tree) – это двоичное дерево поиска, вершины которого разделены на красные (red) и чёрные (black). Таким образом, каждая вершина хранит один дополнительный бит – её цвет [3].

При этом должны выполняться определённые требования, которые гарантируют, что глубины любых двух листьев отличаются не более чем в два раза, поэтому дерево можно назвать сбалансированным (balanced).

Каждая вершина красно-чёрного дерева имеет поля color (цвет), key (ключ), left (левый ребёнок), right (правый ребёнок) и p (родитель). Если у вершины отсутствует ребёнок или родитель, соответствующее поле содержит NIL. Для удобства будем считать, что значения NIL, хранящиеся в полях left и right, являются ссылками на дополнительные (фиктивные) листья дерева. В таком пополненном дереве каждая старая вершина (содержащая ключ) имеет двух детей [3].

Двоичное дерево поиска называется красно-чёрным деревом, если оно обладает следующими свойствами (будем называть их RB-свойствами, по-английски red-black properties):

1. Каждая вершина – либо красная, либо чёрная.

2. Каждый лист (NIL) – чёрный.

3. Если вершина красная, оба её ребёнка чёрные.

4. Все пути, идущие вниз от корня к листьям, содержат одинаковое количество чёрных вершин [1].

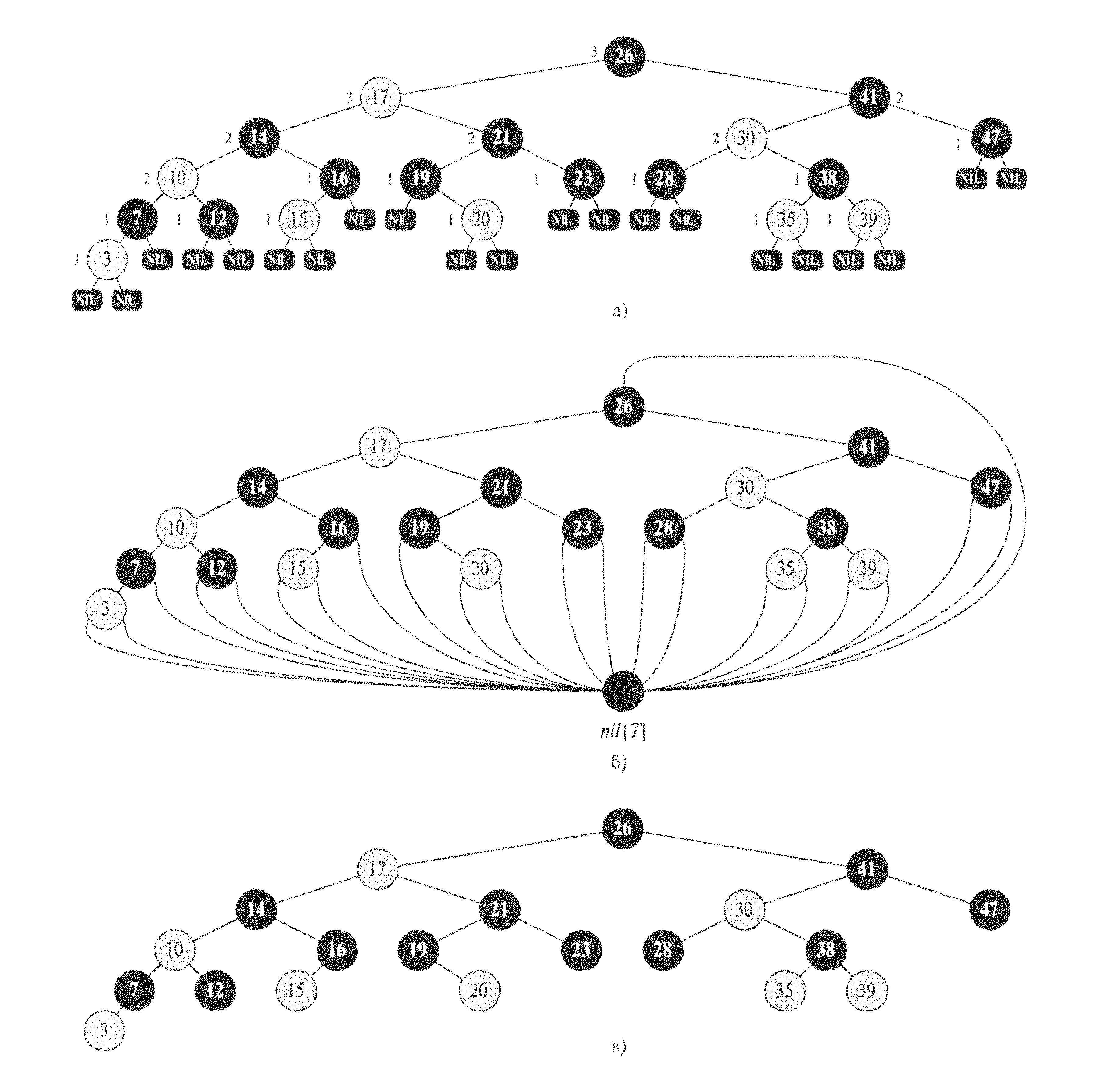
Рис. 7. Красно-чёрное дерево. Чёрные вершины показаны как тёмные, красные – как серые. Каждая вершина либо красная, либо чёрная. Все NIL-листья чёрные. Дети красной вершины – чёрные. Для каждой вершины все пути от неё вниз к листьям содержат одинаковое количество чёрных вершин. Около каждой вершины (кроме листьев) записана её чёрная высота. Чёрная высота листьев равна 0.

Рассмотрим произвольную вершину x красно-чёрного дерева и пути, ведущие вниз от неё к листьям. Все они содержат одно и то же число чёрных вершин (добавим к ним путь из корня в x и применим свойство 4). Число чёрных вершин в любом из них (саму вершину x не считаем) будем называть чёрной высотой (black-height) вершины x и обозначать bh(x). Чёрной высотой дерева будем считать чёрную высоту его корня.

Следующая лемма показывает, что красно-чёрные деревья хороши как деревья поиска.

Лемма. Красно-чёрное дерево с n внутренними вершинами (т.е. не считая NIL-листьев) имеет высоту не больше 2lg(n+1).

Доказательство. Сначала покажем, что поддерево с корнем в x содержит по меньшей мере 2^bh(x)-1 внутренних вершин. Доказательство проведём индукцией от листьев к корню. Для листьев чёрная высота равна 0, и поддерево в самом деле содержит не менее 2^bh(x)-1=2⁰-1=0 внутренних вершин. Пусть теперь вершина x не является листом и имеет чёрную высоту k. Тогда оба её ребёнка имеют чёрную высоту не меньше k-1 (красный ребёнок будет иметь высоту k, чёрный - k-1). По предположению индукции левое и правое поддеревья вершины x содержат не менее 2^k-1-1 вершин, и потому поддерево с корнем x содержит, по меньшей мере, 2^k-1-1+2^k-1-1+1=2^k-1 внутренних вершин.

Чтобы завершить доказательство леммы, обозначим высоту дерева через h. Согласно свойству 3, по крайней мере, половина узлов на пути от корня к листу, не считая сам корень, должны быть черными. Следовательно, черная высота корня должна составлять как минимум h/2; следовательно,

Перенося 1 в левую часть и логарифмируя, получим, что , или .

Непосредственным следствием леммы является то, что такие операции над динамическими множествами, как Search, Minimum, Maximum, Predecessor и SUCCESSOR, при использовании красно-черных деревьев выполняются за время О(lg(h)), поскольку время работы этих операций на дереве поиска высотой h составляет О(h), а любое красно-черное дерево с n узлами является деревом поиска высотой О (lg(n)). Хотя алгоритмы Tree_Insert и Tree_Delete характеризуются временем работы О(lg(n)), если использовать их для вставки и удаления из красно-черного дерева, непосредственно использовать их для выполнения операций Insert и Delete нельзя, поскольку они не гарантируют сохранение красно-черных свойств после внесения изменений в дерево [3].