Лекція 3

Залежність швидкості реакції від температури

Як відомо, швидкість величезної більшості хімічних реакцій стрімко зростає із збільшенням температури. Саме тому нагрівання є дуже поширеним прийомом, як у хімічній практиці, так і в інших галузях: техніці, кулінарії, побуті і фармації зокрема. З цим явищем ми стикаємось і в біології: при зниженні температури усі процеси в деяких організмах суттєво сповільнюються і вони переходять у стан анабіозу.

За законом діючих мас:

(4)

Отже, вплив температури може здійснюватись через зміну концентрації, через порядок реакції і через зміну константи швидкості реакції. З досвіду відомо, що основний вплив температура вчиняє на константу швидкості. Тому, кажучи про вплив температури на швидкість,мають на увазі зміну константи швидкості.

Для багатьох хімічних реакцій, що протікають у інтервалі 0-100 ºС, справедливе емпіричне правило Вант-Гоффа: при підвищенні температури на 10 ºС (10 К) швидкість реакції зростає у 2-4 рази. Відношення швидкості реакції при температурі Т до швидкості при температурі Т+10 називають температурним коефіцієнтом Вант-Гоффа .

(31)

У випадку, коли зміна температури не рівна 10 ºС, зручно користуватися рівнянням:

(32)

ПравилоВан-Гоффа наближене і не враховує залежність температурного коефіцієнта від температури, оскільки, , при зростанні температури, прямує до одиниці.

Голландський учений Арреніус експериментально встановив більш точну залежність константи швидкості від температури:

(33)

В сучасному вигляді рівняння Арреніуса (32) представляють:

, (34)

або:

(35)

Або у диференційній формі:

(36)

Коефіцієнт рівняння k₀ - передекспоненційний множник, має розмірність константи швидкості відповідного порядку. Для елементарних реакцій k₀ можна розрахувати теоретично використовуючи молекулярно-кінетичну теорію та статистичну термодинаміку. Цей коефіцієнт дещо залежить від температури, але цією залежністю можна знехтувати порівняно з

Константа рівнянь (34-36) E має розмірність Дж/моль і носить назву енергія активації реакції. Хоча теоретичне обґрунтування рівняння Арреніуса виконане лише для елементарних реакцій, досвід показує, що, більшість складних реакцій також підпорядковуються даному рівнянню. У цьому випадку, енергія активації – це мінімальна надлишкова, у порівнянні з середнім рівнем,кількість енергії, яку треба надати 1 молю речовини, щоб вона вступила ухімічне перетворення.

В часи Арреніуса енергія активації розглядалась як суто емпірична константа, однак зараз, для елементарних реакцій, її можна оцінити з допомогою квантової хімії. Емпіричне рівняння (35), у наш час, також можна вивести для елементарних реакцій на основі теорії перехідного стану (активованого комплексу). Згідно з цією теорією енергія активації приблизно дорівнює перевищенню середньої енергії активованого комплексу над середньою енергією вихідних речовин. Для реакції А↔В , енергії активації прямої і зворотної реакцій пов’язані співвідношенням . Відповідно, для екзотермічної реакції , ; для ендотермічної і .

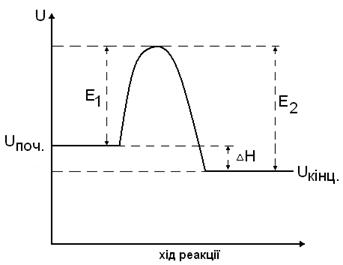
Рис.14.Зміна енергії під час екзотермічної реакції

Рис.15.Зміна енергії під час ендотермічної реакції

Для знаходження енергії активації реакції необхідно експериментально визначити константишвидкості хоча б при двох температурах:

(а),

(б)

Розділимо (б) на(а) і дістанемо:

(37)

Точніше енергію активації знаходять графічно, побудувавши за експериментальними даними залежність . З рівняння (34) видно, що кутовий коефіцієнт отриманої прямої , а відрізок, що відсікається на осі ординат – дорівнює k₀ .

Рис.16.Графічне визначення енергії активації та передекспоненційного множника

Величина енергії активацій реакцій, які підпорядковуються, правилу Вант-Гоффа і протікають при температурі ≈300К лежить у межах 50-100 кДж/моль.

Існують реакції для яких рівняння Арреніуса та правило Вант-Гоффа не підтверджуються. Це реакції з нетермічним характером активації, гетерогенні реакції, що протікають у дифузійній області, а також деякі специфічні реакції, як, наприклад, реакція окиснення оксиду азоту: 2NO + O₂ =2NO₂ , для якої характерне зменшення швидкості при збільшення температури.