2.2.2. Свободные колебания неконсервативной системы (с затуханием)

При выводе уравнений свободных колебаний консервативной системы влияние диссипативных сил не рассматривалось. В соответствие с этим получено, что свободные колебания могут продолжаться сколь угодно долго. В действительности колебания постепенно затухают ввиду наличия сил сопротивления (сопротивление воздуха, жидкости, трение в подшипниках, а также внутреннее трение в материале и т.д.). Рассмотрим вязкое демпфирование, так как оно является простейшим с математической точки зрения. Будем рассматривать вязкое демпфирование или демпфирующую силу, величина которой изменяется пропорционально колебательной скорости.

Рассмотрим сосредоточенную систему с одной степенью свободы, состоящую из пружины, сосредоточенной массы и жидкостного демпфера (рис. 2.13). Полагаем, что пружина и демпфер не обладают массой.

Дифференциальное уравнение поступательного движения тела имеет вид

или

Коэффициент h представляет собой коэффициент линейного вязкого демпфирования и имеет размерность в системе СИ (Н·с/м). Знак минус перед демпфирующей силой означает, что эта сила всегда имеет направление, противоположное направлению колебательной скорости. Разделив последнее выражение на m, и введя обозначения

_с² = c/m; 2 = h/m,

п олучим уравнение свободных колебаний с вязким демпфированием

Величина  называется коэффициентом затухания или коэффициентом демпфирования. Размерность  совпадает с размерностью круговой частоты собственных колебаний _с.

Дифференциальное уравнение (2.37) является однородным линейным уравнением второго порядка с постоянными коэффициентами. Как известно, его решение следует искать в форме

s = Ce^t,

где e – основание натурального логарифма; t – время;  – постоянная величина, определяемая из условия того, что последнее выражение должно удовлетворять уравнению (2.37). Продифференцировав два раза последнее выражение и подставив в уравнение (2.37), получим характеристическое уравнение

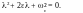
Корни характеристического уравнения равны

Колебательный процесс определяется соотношениями между значениями  и _с.

Возможны три случая:

 < _с. Это случай малого сопротивления – корни уравнения (2.38) являются комплексно-сопряженными.

 = _с. Критическое сопротивление – корни уравнения (2.38) кратные.

 > _с. Большое сопротивление – уравнение (2.38) имеет два отрицательных вещественных корня.

1. Малое сопротивление. Если  < _с, то величина под знаком квадратного корня в (2.38) отрицательна. Обозначим _з = (²_с – ²)^½, которая называется условной частотой затухающих колебаний. Тогда из (2.38) получим следующие значения для корней характеристического уравнения:

_1,2 = –  ± i_з.

Подставляя значения ₁ и ₂ в выражение s = Ce^t, получим два решения уравнения (2.37):

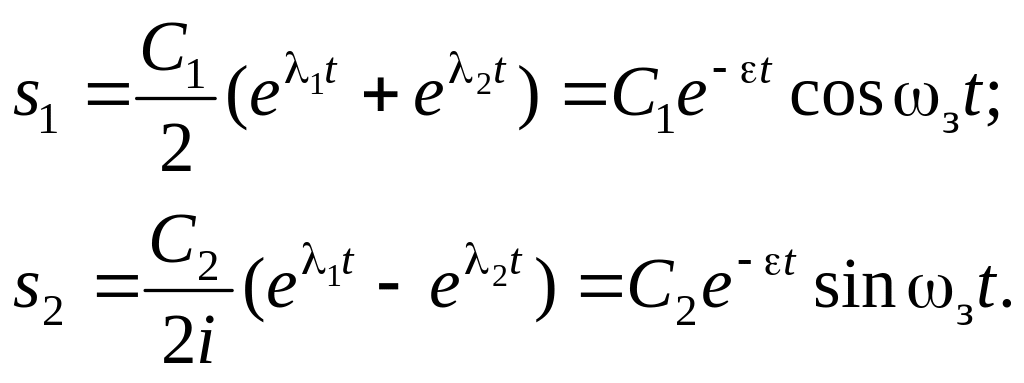
Соответственно общее решение дифференциального уравнения (2.37) будет суммой этих решений

s = e^–·t(C₁ cos_зt + C₂ sin_зt), (2.39)

где C₁ и C₂ – произвольные постоянные, которые должны определяться из начальных условий.

В амплитудной форме решение (2.39) выглядит как

s = A e^–·t sin(_зt + ), (2.40)

где A и  – тоже произвольные постоянные.

Раскрывая синус суммы, имеем

s = A e^–·t sin(_зt + ) = e^–·t(A sincos_зt + A cossin_зt).

Из сопоставления последнего выражения и формулы (2.39), получаем формулы связи постоянных интегрирования:

C₁ = A sin; C₂ = A cos,

и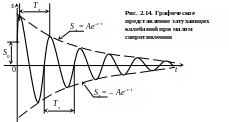 ли A = (C₁² + C₂²)^½; sin = C₁/A; cosC₂/A; tg = C₁/C₂.

Постоянные C₁, C₂ и соответственно A,  определяются из начальных условий: t = 0; s = S₀; ś = Ś₀.

Дифференцируя (2.39) по времени, получим

ś = –·e^–·t(C₁cos_зt+C₂sin_зt)+e^–·t(–C₁_зsin_зt+C₂_зcos_зt). (2.41)

Используя выражение (2.39) для s, а (2.41) для ś при t = 0, получим уравнения для определения C₁ и C₂:

C₁ = S₀; Ś₀ = – ·C₁ + ₁·C₂.

Откуда

C₁ = S₀; C₂ = (Ś₀ +·S₀)/_з = (Ś₀ +·S₀)/(_с² – ²)^½.

У читывая начальные условия, постоянные А и  будут иметь вид

Подставляя найденные значения С₁ и С₂ в решение (2.39), получим

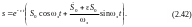
В этом выражении первое слагаемое определяется начальным перемещением S₀, а второе слагаемое зависит от начального перемещения S₀ и от начальной скорости Ś₀.

Для графической интерпретации решения (2.40) построим ее зависимость, которая изображена на рис. 2.14.

К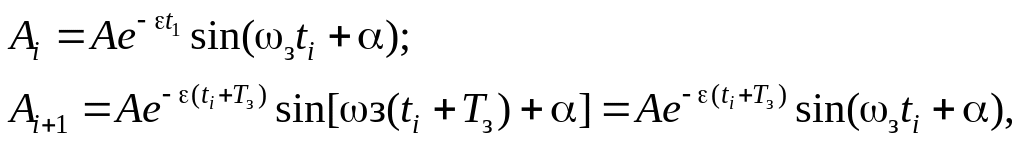 роме основной зависимости на рис. 2.14 представлены вспомогательные функции S₁ = Ae^-·t и S₂ = – A e^-·t. Данные кривые являются ограничивающими для кривой sin(_зt + ). Из рис. 2.14 следует, что величины последовательных наибольших отклонений s от положения равновесия уменьшаются с течением времени и стремятся к нулю. Колебания такого типа называются затухающими.

Величину T_з = 2/_з = 2_с^^^½называют условным периодом затухающих колебаний, а _з – условной частотой затухающих колебаний. Величину Ae^–·t можно назвать условной амплитудой затухающих колебаний.

Из анализа уравнения (2.40) следует, что при малых значениях коэффициента затухания ( << _с) условная частота затухающих колебаний ₁ ≈_сследовательно и T_з ≈ T.

Не являясь чисто периодическим движением, затухающие колебания чередуются через равный промежуток времени T_з, то есть получают периодически максимальные и нулевые значения. Поэтому их можно классифицировать как условно-периодические.

Декремент колебаний. Если в выражение Ae^-·t подставить значение ₀ = 1/ = Т₁/2, называемую постоянной времени затухающих колебаний и измеряемую в рад/с, то последовательность амплитуд колебаний с периодом ₀ будет следующим (начиная с t=0):

То есть амплитуда затухающих колебаний за каждый период уменьшается в e раз. Через 3₀ условная амплитуда уменьшится в e³, то есть примерно в 20 раз. Как правило, считается, что по истечении времени 3-х периодов затухающие колебания прекращаются.

Введем понятие декремента колебаний , которым называют отношение двух последовательных амплитудных значений. Пусть

где t_i – время, соответствующее i-му максимуму координаты.

Исходя из этого, декремент колебаний равен

Логарифмическим декрементом колебаний  называют натуральный логарифм от декремента колебаний:

 = ln = ·T_з.

С помощью  экспериментально находят коэффициент затухания , используя соотношение двух соседних амплитуд

П овысить точность определения  можно, если использовать соотношения двух амплитуд, отделенных j циклами согласно выражению

Экспериментально определяются T_з, последовательные значения A_i и A_i+1 и вычисляется .

2. Критическое сопротивление ( = _с). В этом случае

_1,2 = – .

При кратных корнях общее решение дифференциального уравнения (2.37) имеет вид

s = C₁e^-·t + C₂ t e^-·t = e^-·t(C₁ + C₂·t). (2.43)

Произвольные постоянные C₁ и C₂ определяются из начальных условий при t = 0 s(0) = S₀, ś(0) = Ś₀

С₁ = S₀; C₂ = Ś₀ + ·S₀. (2.44)

Р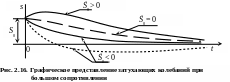 ешение (2.43) представляет собой произведение экспоненты в отрицательной степени и линейной функции времени. известно, что экспонента в отрицательной степени убывает быстрее, чем возрастает любая степенная функция. Поэтому это решение обратится в нуль только единожды, если константы С₁ и С₂ имеют разные знаки. Исходя из (2.44) начальное отклонение и начальная скорость должны иметь разные знаки и при этом должно выполняться условие |Ś₀| > ·|S₀|.

Вне зависимости от начальных условий движение при критическом сопротивлении не имеет колебательного характера (рис. 2.15). Такое движение называют апериодическим. Причем, чем меньше начальная скорость Ś₀, тем быстрее уменьшается амплитуда полупериода колебаний. Хотя с инженерной точки зрения сложно воспроизвести собственные колебания с начальными условиями Ś₀ > 0 или Ś₀ < 0. Как правило, понятными являются начальные условия, когда Ś₀ = 0.

3. Большое сопротивление ( > _с). В этом случае

_1,2 = –  ± k, где k = (² – _с²)^½. Поскольку k < , оба корня характеристического уравнения будут отрицательными. Общее решение дифференциального уравнения (2.37) для данного вида демпфирования имеет вид

Произвольные постоянные С₁ и С₂ определяются также из начальных условий:

Движение в случае большого сопротивления также имеет апериодический характер. Но с увеличением демпфирования в системе (), время окончательного затухания возрастает и кривые зависимости s(t) растягиваются по времени (рис. 2.16), поскольку с повышением вязкого сопротивления скорость движения убывает.