Занятие 1. «Кинематика материальной точки»
1. Радиус-вектор частицы определяется
выражением
(м). Найти
и
-
?.
2. Начальное значение радиус-вектора
равно
(м),
конечное
(м).
Найти: а) приращение радиус-вектора
;
б) модуль приращения радиус-вектора
.
3. Написать выражение для косинус
угла
между векторами с компонентами
и
.
4. Радиус-вектор частицы изменяется
со временем по закону
(м).
Найти: а) скорость
и ускорение
частицы; б) модуль скорости
в момент времени
с;
в) приближенное значение пути
,
пройденного частицей за 11-ю секунду
движения.
5. Начальное значение скорости равно
(м/с), конечное
(м/с). Найти: а) приращение скорости
;
б) модуль приращения скорости
;
в) приращение модуля скорости
.
6. Компоненты одного вектора равны
,
другого
.
Найти угол
между векторами.
7. Радиус-вектор частицы определяется
выражением
(м).
Вычислить: а) путь
,
пройденный частицей за первые 10 секунд
движения; б) модуль перемещения
за то же время.
8. Частица движется со скоростью
(м/с).
Найти: а) перемещение
частицы за первые 2 секунды ее движения;
б) модуль скорости
в момент времени
с.
Занятие 2. «Кинематика материальной точки»
1. Точка движется в плоскости
по закону:
,
,
где
и
– положительные постоянные,
– время. Найти: а) уравнение траектории
точки
,
изобразить ее график; б) модуль скорости
и модуль ускорения
точки в зависимости от времени; в) момент
,
в которой вектор скорости составляет
угол
с вектором ускорения. (Ответ:
,
,
,
)
2. Тело бросили с поверхности Земли
под углом
к горизонту с начальной скоростью
.
Пренебрегая сопротивлением воздуха
найти: а) время движения
;
б) максимальную высоту подъема
и горизонтальную дальность полета
,
при каком значении угла
они будут равны; в) уравнение траектории
,
где
и
–
перемещения тела по вертикали и
горизонтали соответственно; г) полное,
тангенциальное и нормальное ускорение
в начале и середине траектории; д) радиус
кривизны
начала и вершины траектории.
3. Пушка и цель находятся на одном
уровне на расстоянии 5,10 км друг от дуга.
Через сколько времени снаряд с начальной
скоростью 240 м/с достигнет цели в
отсутствие сопротивления воздуха?
(Ответ:
с)
4. Тело брошено под углом
к горизонту с начальной скоростью
м/с. Найти: а) максимальную высоту подъема
и горизонтальную дальность полета; б)
под каким углом
к горизонту движется тело через
с
после начала движения? Через
с? в) через сколько времени
и на какой высоте
тело будет двигаться под углом
к горизонту?
(Ответ: а)
м,
б)
,
;
в)
с
)
5. Снаряд, выпущенный из орудия под
углом
к горизонту, дважды был на одной и той
же высоте
спустя время
с и
с после выстрела. Определить начальную
скорость
и высоту
.
(Ответ:
м/с;
м)
6. Над колодцем глубиной
м
бросают вертикально вверх камень с
начальной скоростью
м/с. Через сколько времени камень
достигнет дна колодца? (Ответ:
)
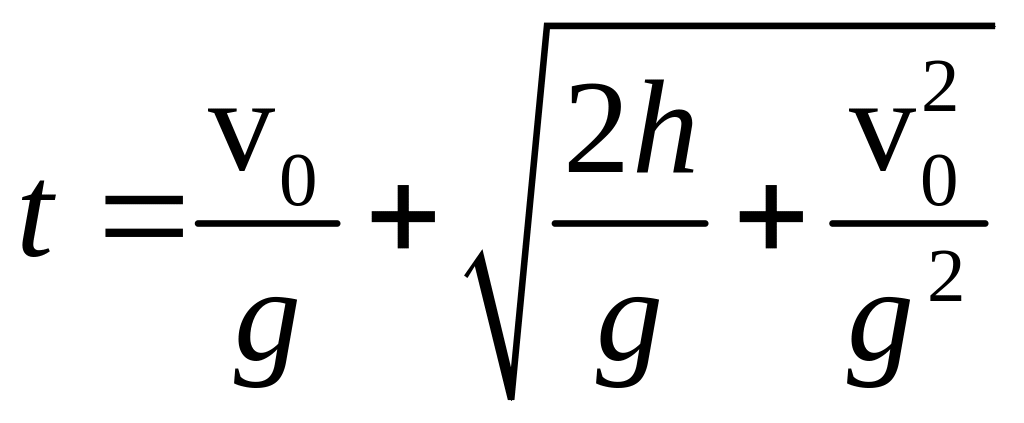7. Точка движется в плоскости
по закону
,
,
где
и
– положительные постоянные,
– время. Найти: а) путь
,
проходимый точкой за время
;
б) угол между векторами скорости и
ускорения точки. (Ответ:
;
)
8. Тело брошено со скоростью
м/с под углом 300к горизонту.
Пренебрегая сопротивлением воздуха,
определите для момента времени
с
после начала движения: 1) нормальное
ускорение; 2) тангенциальное ускорение.
9. Точка движется, замедляясь, по
прямой с ускорением, модуль которого
зависит от ее скорости
по закону
,
где
–
положительная постоянная. В начальный
момент скорость точки равна
.
Какой путь она пройдет до остановки? За
какое время этот путь будет пройден?
10. Из пушки выпустили последовательно
два снаряда со скоростью
м/с:
первый - под углом
к горизонту, второй – под углом
(азимут один и тот же). Пренебрегая
сопротивлением воздуха, найти интервал
времени между выстрелами, при котором
снаряды столкнутся друг с другом. (Ответ:
)