Вычисление длины плоской кривой. Основные формулы

Если плоская кривая задана как график функции y = f(x), a ≤ x ≤ b, и производная y = f (x) непрерывна, то длина дуги этой кривой выражается интегралом

l = = .

Если кривая задана параметрически x = x(t), y = y(t),  ≤ t ≤  и производные x (t) и y (t) непрерывны на отрезке [, ], то длина дуги кривой выражается интегралом

l = .

Если кривая задана уравнением r = r(),  ≤  ≤ , в полярных координатах и r () непрерывна на отрезке [, ], то длина l дуги кривой выражается интегралом

l = .

Если Г – пространственная кривая, заданная параметрически: x = x(t), y = y(t), z = z(t),  ≤ t ≤ , производные x (t), y (t) и z (t) непрерывны на отрезке [, ], то длина Г находится по формуле

l = .

Замечание. Пусть Г – некоторая кривая на плоскости xOy. Выра­жение

dl = ,

где dx² = (dx)², dy² = (dy)², называется дифференциалом длины дуги. Используя это понятие, можно единообразно записать формулу для вычисления длины кривой

l = = ,

где  и ,  ≤ , обозначают границы изменения параметра, с помощью которого задается кривая. Пусть кривая Г есть график функции x = x(y), c ≤ y ≤ d. Тогда dx = x (y) dy и мы получаем

l = = .

Если кривая Г задана параметрически, то dx = x (t) dt, dy = y (t) dt и мы получаем

l = = = .

Задание кривой с помощью полярных координат r = r(),  ≤  ≤ , есть частный случай параметрического задания: x = r()cos , y = = r() sin . Параметром здесь является . Вычисляя дифференциалы dx = (r cos  – r sin ) d, dy = (r sin  + r cos ) d, убеждаемся, что dl = = .

Для пространственной кривой Г дифференциалом длины дуги называется выражение l = и длину кривой Г можно выразить интегралом

l = = ,

где  и  ( ≤ ) – концы отрезка [, ] – промежутка изменения параметра, с помощью которого задается кривая.

Рассмотрим примеры.

Вычислить длину дуги кривой.

5.19. y = 1 – ln cos x, 0 ≤ x ≤ .

5.20. y = 2 , 0 ≤ x ≤ 1.

5.21. x = , 0 ≤ y ≤ 4.

5.22. 3y² = x(x – 1)² (длину петли).

5.23. y = , 0 ≤ x ≤ ln 4.

5.24. y = , 0 ≤ x ≤ .

Решение.

5.19. Так как y = = tg x, то

.

5.20. Так как , то

.

Можно было рассмотреть нашу кривую как график функции , . Тогда вычисление длины кривой свелось бы к нахождению интеграла

.

5.21. Вычисляем производную = и далее = = , откуда

= = = .

5.22. Из условия следует, что y = 0 при x = 0 и x = 1, причем линия симметрична относительно оси Ox, так как y входит в уравнение в четной степени. Ясно, что достаточно вычислить длину половины петли, задаваемой уравнением y = , . (Вторая половина петли есть график функции ). Так как

, =  ,

то мы получаем

= = .

5.23. Делаем предварительные вычисления:

= – = .

Вычисляем длину кривой

l = = = = 2.

5.24. Вычисляем производную:

= ,

тогда

= = .

Вычисляем длину кривой

l = = = =

= = = =

= .

Вычислить длину кривой, заданной в полярных координатах.

5.25. r = , – ≤  ≤ .

5.26. r = a(1 + cos ), 0 ≤  ≤ 2π (кардиоида).

5.27. r = th , 0 ≤  ≤ 2.

5.28. r = a cos⁴ .

Решение.

5.25. Вычисляем длину кривой по формуле

l = = = =

= = = .

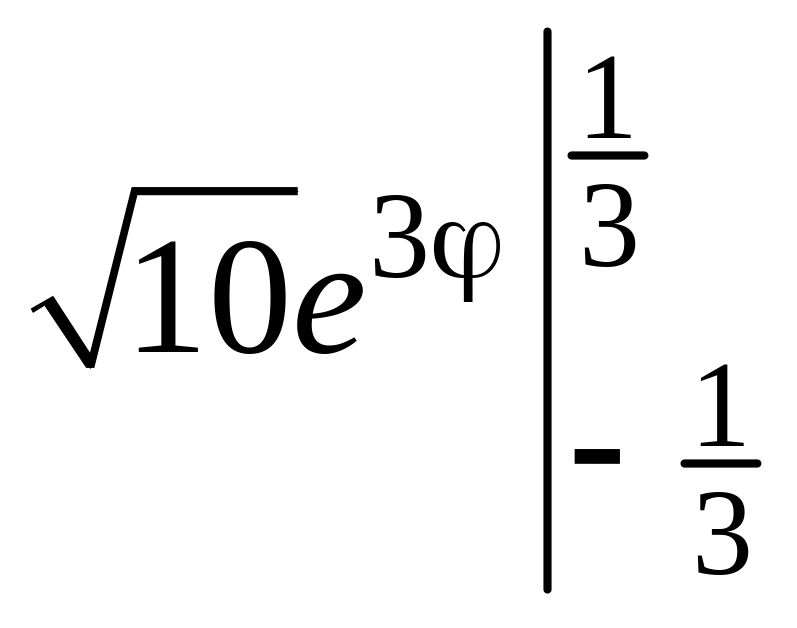5.26.

l = = =

= = = – =

=  – = 4a + 4a = 8a.

5.27.

l = = =

= = = =

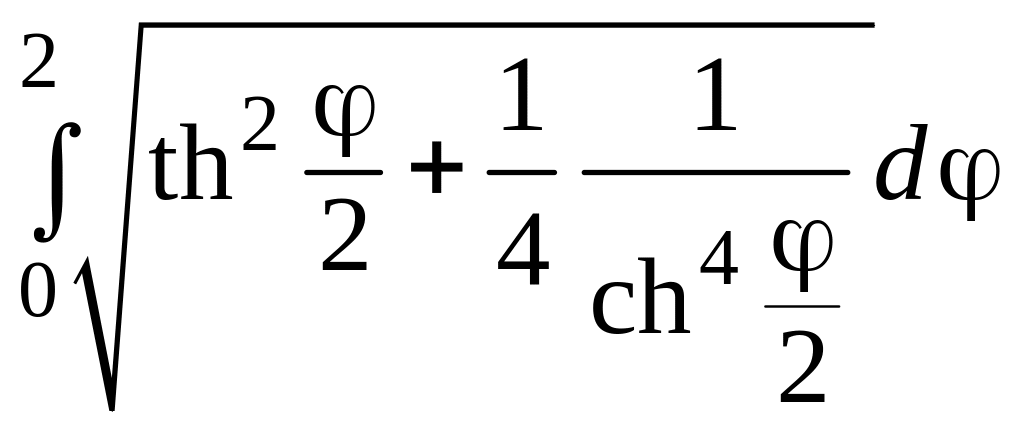= = = = 1 – th1.

5

Рис. 2.16

.28. Функция cos имеет период 8π. Функции , cos² , cos⁴ и т.п. имеют период 4π. Поскольку = , то линия симметрична относительно полярной оси и при изменении  от 0 до 2π полярный радиус опишет половину линии. Найдем длину половины кривой (рис. 2.16) и затем удвоим результат. Вычисляем

= a² + = .

Отсюда следует

l = = = =

=  = .

Вычислить длину кривой, заданной параметрически.

5.29. x = 6t⁵, y = 5t(1 – t⁸), 0 ≤ t ≤ 1.

5.30. x = ln(1 + t²), y = 2arctg t – 2t + 8, 0 ≤ t ≤ 1.

5.31. x = t – sh 2t, y = 2 ch t, 0 ≤ t ≤ 1.

5.32. x = 2 cos³ t, y = 2 sin³ t.

5.33. x = t², y = t – t³ (длину петли).

Решение.

5.29. Вычисляем, используя соответствующую формулу:

l = = =

= 5 = 5 = = 10.

5.30.

= + = .

Поэтому

l = = = .

5.31.

= (1 – ch 2t)² + 4sh²t = | ch 2t – 1 = 2 sh² t | = 4 sh⁴ t + 4sh² t =

= 4 sh² t ch² t = sh² 2t.

Поэтому

l = = = = sh² 1.

5.32. Уравнение линии (астроиды) в декартовых координатах имеет вид или (рис. 2.17).

О

Рис. 2.17

тсюда следует, что линия симметрична относительно обеих осей координат. Вычислим четверть длины астроиды, что соответствует изменению параметра t от 0 до , и результат учетверим. Вычисляем

= 36 cos⁴ t sin² t + 36 sin⁴ t cos² t =

= 36 sin² t cos² t = 9 sin² 2t.

Отсюда следует

l = = = 6 + 6 = 12.

5.33. Если выразить y через x, то мы получаем

,

откуда следует, что при x  [0, ] графики симметричных относительно оси Ox функций

и

образуют замкнутый контур на плоскости xOy (петлю). График функции

получается, когда t изменяется от –1 до 0, а при изменении t от 0 до 1 точка (x, y) движется по графику функции

от точки O (0, 0) до точки A( , 0).

Вычисляем сначала = 12t² + (1 – 3t²)² = (1 + 3t²)². Поэтому

l = = = 4.

Вычислить длину дуги пространственной кривой.

5.34. x = 3t – t³, y = 3t², z = 3t + t³, 0 ≤ t ≤ 1.

5.35. x = at, y = , z = , ≤ t ≤ 1.

5.36. x = e^t, y = e^-t, z = t, 0 ≤ t ≤ 2.

5.37. x = a (1 + cos t), y = a(t – sin t), z = 4 a sin , 0 ≤ t ≤ 2.

Решение.

5.34. Вычисляем длину кривой по формуле

l = = =

= = = = 4 .

5.35.

= =

=  = = .

Отсюда получаем

l = = = = .

5.36. Имеем = e^2t+ e^–2t +2 = (e^t + e^–t)². Откуда получаем

l = = = = 2 sh 2.

5.37. Сделаем предварительные вычисления:

= 4 =

= = 4a².

Мы использовали здесь тригонометрическую формулу 1 – cos t = =  .

Вычисляем длину кривой

l = = 4a.

Вычисление объемов и площадей поверхностей. Основные формулы.

Пусть S(x) – площадь сечения тела V плоскостью, перпендикулярной к оси Ox в точке с абсциссой x, a и b – левая и правая границы изменения x. Тогда объем тела V выражается интегралом

V = .

Если тело V образовано вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой y = f(x) ≥ 0, a ≤ x ≤ b, осью абсцисс и прямыми x = a, x = b, то объем тела V вычисляется по формуле

V = = .

Если тело образовано вращением вокруг оси Oy криволинейной трапеции, образованной подграфиком функции x = g(y), c≤ y ≤ d (g(y) ≥ 0), то объем тела выражается интегралом

V = = .

Если вокруг оси Oy вращается криволинейная трапеция, ограниченная графиком функции y = f(x) ≥ 0, a ≤ x ≤ b, осью абсцисс и прямыми x = a, x = b, то объем получившегося тела выражается интегралом

V = = .

Если кривая задана параметрически или в полярных координатах, то следует сделать соответствующую замену переменных в указанных выше формулах.

Площадь поверхности, образованной вращением вокруг оси Ox дуги Г кривой y = f(x), a ≤ x ≤ b, где f(x) имеет на отрезке [a, b] непрерывную производную , выражается интегралом

S = = .

Поскольку – дифференциал длины дуги, то формулу можно записать в виде

S = .

Пусть кривая задана параметрически x = x(t), y = y(t),  ≤ t ≤ , где функции x(t) и y(t) имеют на отрезке [, ] непрерывные производные x(t) и y(t). Площадь S поверхности, образованной при вращении данной кривой вокруг оси Ox равна

S = = .

Задание кривой с помощью полярных координат r = r(),  ≤  ≤ , есть частный случай параметрического задания, так как в этом случае

x = r() cos , y = r() sin .

Рассмотрим примеры.

5.38. На всех хордах круга радиуса R, параллельных одному направлению, построены симметричные параболические сегменты постоянной высоты h (рис. 2.18). Плоскости сегментов перпендикулярны к плоскости круга. Найти объем образованного таким образом тела.

а б

Рис. 2.18

Решение. Найдем вначале площадь параболического сегмента с основанием a и высотой h (рис. 2.18, б). Расположим оси координат так, что основание сегмента будет находиться на оси абсцисс и начало координат делит это основание пополам. Уравнение параболы имеет вид

.

Так как y(0) = h, то  = – . Тогда уравнение параболы принимает вид

.

Ищем площадь сегмента

S = = = = ah.

Расположим оси координат так, как показано на рис. 2.18, а. Тогда длина половины хорды, пересекающей ось абсцисс в точке x, есть . Следовательно, площадь параболического сегмента, соответствующего значению x, равна S(x) = . Согласно формуле для объема, получаем

V = = = =

= = = .

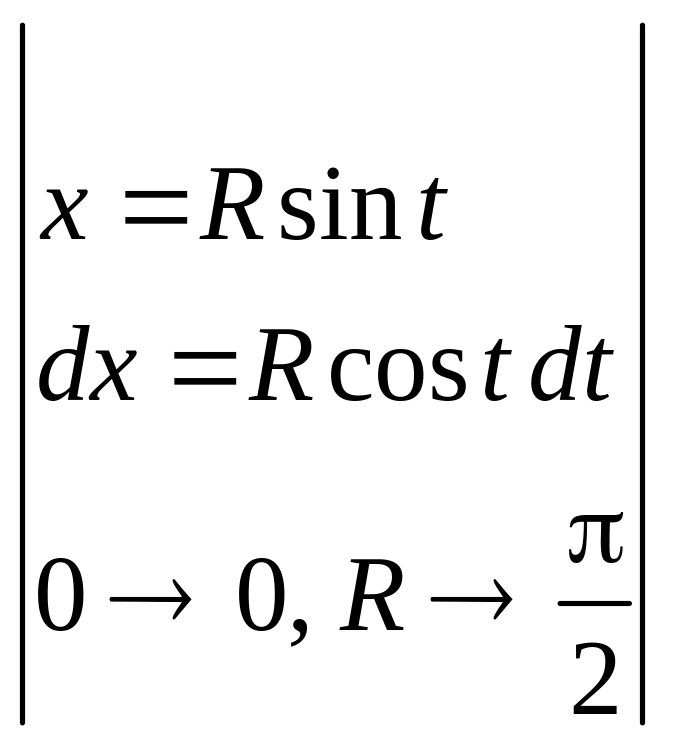5.39. Найти объем тела, ограниченного поверхностями z = 4 – y², x = 0, x = a, y = 0, z = 0.

Р

Рис. 2.19

ешение. Найдем площадь сечения тела плоскостью, перпендикулярной к оси Ox, (0 ≤ x ≤ a) (рис. 2.19). Нам необходимо знать площадь половины параболического сегмента с a = 2, h = 4. Как мы знаем из решения предыдущей задачи, эта площадь равна

S(x) = = , 0 ≤ x ≤ a.

Отсюда получаем

V = = = .

Найти объем тела, образованного вращением фигуры, ограниченной следующими линиями.

5.40. y = sin x, x = 0, 0 ≤ x ≤ π, вокруг оси: а) Ox, б) Oy.

5.41. y = 2^x, y = , x = 0, y = 0, вокруг оси Ox.

5.42. y = x(3 – x), y = x, вокруг оси: а) Ox, б) Oy.

5.43. y = cos x, y = 1, 0 ≤ x ≤ 2π, вокруг оси Oy.

5.44. y = e^x+6, y = e^2x, x = 0, вокруг оси: а) Ox, б) Oy.

5.45. y = , y = 0, x ≥ 1, вокруг оси Ox.

5.46. y = , y = 0, x ≥ 0, вокруг оси Ox.

5.47. y = , y = 0, вокруг оси Oy, .

5.48. x = 4t², y = (петля), вокруг оси Ox.

5.49. x = a ch³ t, y = a sh³ t, x = 2 a, вокруг оси Ox.

5.50. r = 2cos² , вокруг полярной оси.

5.51. r = , 0 ≤  ≤ , вокруг полярной оси.

Решение.

5.40. Вычислим объем полученный вращением вокруг оси Ox. Имеем

V = = = .

Теперь вычислим объем тела, получаемого при вращении фигуры вокруг оси Oy:

V = = = =

=  .

5.41. Абсцисса точки пересечения графиков (рис. 2.20) равна 1. Искомый объем выражается суммой двух интегралов:

V = + = + .

В

Рис. 2.20

ычислим интегралы с логарифмом отдельно, применяя формулу интегрирования по частям. Имеем

= =

= .

= =

= – =

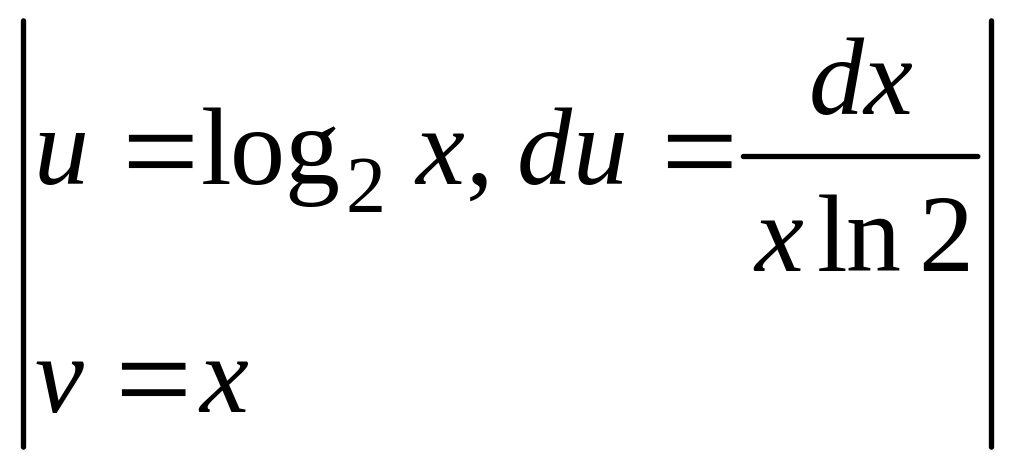= – + + С.

Отсюда получаем,

V = + 12π – + =

Рис. 2.21

= – + – 4π.

5.42. Несложно находится абсцисса точки пересечения графиков x = 2 (рис. 2.21). Вычисляем объем, получаемый при вращении фигуры вокруг оси Ox:

V = =

= =

= = .

При вычислении объема, получающегося при вращении вокруг оси Oy, воспользуемся следующей формулой:

V = – ,

где y₁ = 3x – x², y₂ = x.

Тогда

V = – = = .

5.43. Рассмотрим два способа вычисления искомого объема.

а б

Рис. 2.22

Решение уравнения cos x = y при 0≤ x ≤ π относительно x есть x = arccos y, решением уравнения cos x = y при π ≤ x ≤ 2π является x =2π – arccos y. Тогда объем можно вычислить следующим образом (рис. 2.22, б):

V = = =

= = 4π³.

Но можно, используя другую формулу, вычислять объем и так (рис. 2.22, а), где :

V = 8π³ – = 8π³ – =

= 8π³ – 4π³ = 4π³,

где слагаемое 8π³ есть объем цилиндра, у которого в основании – круг радиуса 2π и высота равна 2.

5

Рис. 2.23

.44. Абсцисса точка пересечения графиков равна ln 3 (рис. 2.23).

Вычисляем вначале объем тела, получаемого при вращении фигуры вокруг оси Ox.

V = =

= = (8 + 36 ln 3) .

Для вычисления объема тела, получаемого вращением фигуры вокруг оси Oy, мы, чтобы не искать обратные функции, воспользуемся следующей формулой:

V = – ,

где y₁ = e^x + 6, y₂ = e^2x.

Тогда

V = + – = 6π ln² 3 + –

= = 6π ln² 3 + =

= 3π ln 3(ln 9 – 1).

5.45. Объем тела выражается несобственным интегралом

V = = = .

5.46. Вычисляем объем

V = = = =

= = .

5.47. Объем можно вычислить двумя способами.

Найдя обратную функцию (x ≥ 0), из уравнения y = , x = , приходим к интегралу

V = .

Можно использовать формулу

V = = = = = π.

Мы видим, что в этом примере второй способ вычисления предпочтительнее.

5.48. Петля симметрична относительно оси Ox, верхняя часть петли есть график функции

y = , 0 ≤ x ≤ 12,

и соответствует изменению параметра t от 0 до . Вычисляем объем

V = = =

= = 48π.

5.49. В декартовых координатах уравнение линии выглядит так: = . Отсюда заключаем, что линия симметрична относительно оси Ox, ясно так же, что a≤ x ≤ a. Верхняя ветвь (y ≥ 0) соответствует изменению параметра t от 0 до (решения уравнений ). Вычисляем объем тела, полученного вращением вокруг оси Ox верхней ветви кривой (y ≥ 0),

V = =

=

5.50. Линия представляет собой два симметричных относительно оси Oy лепестка, симметричных, в свою очередь, относительно оси Ox (рис. 2.24). Первый соответствует изменению параметра  от – до , второй – от до π и от –π до – . Вычислим объем тела, получаемого вращением половины лепестка, и удвоим результат:

V = =

Рис. 2.24

= = =

= = =

= = = = .

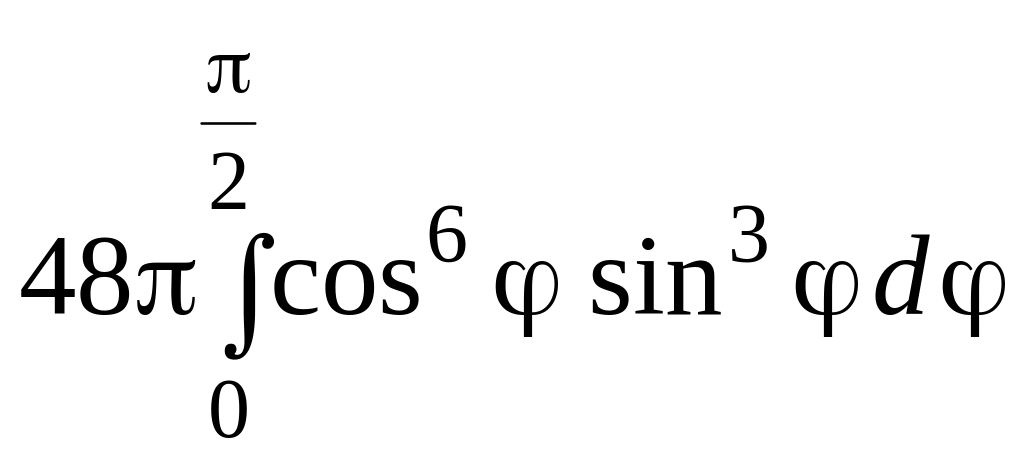Минус перед первым интегралом поставлен потому, что x = r cos  = = 2 cos³ при изменении  от 0 до убывает. Действительно,

V = = =

= = .

5.51. Вычисляем объем при :

V = = = =

= = =

=  = .

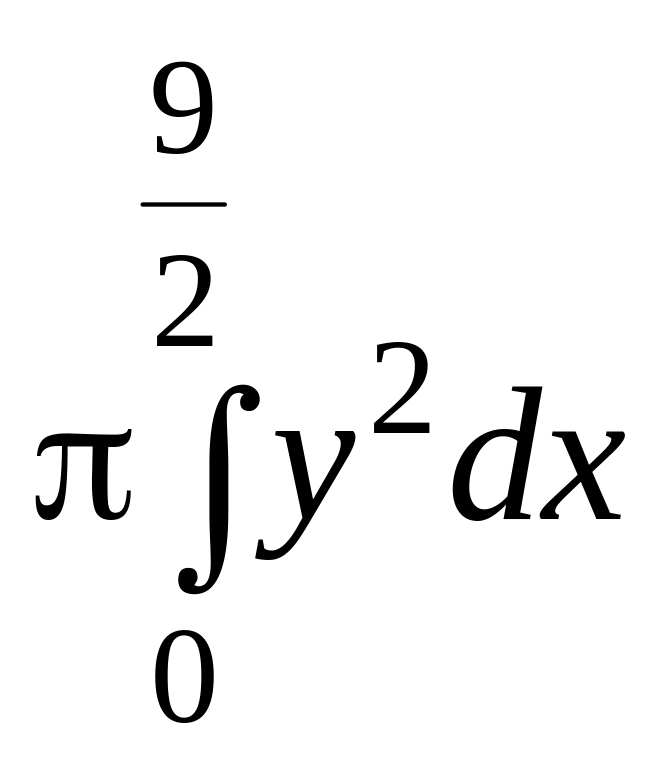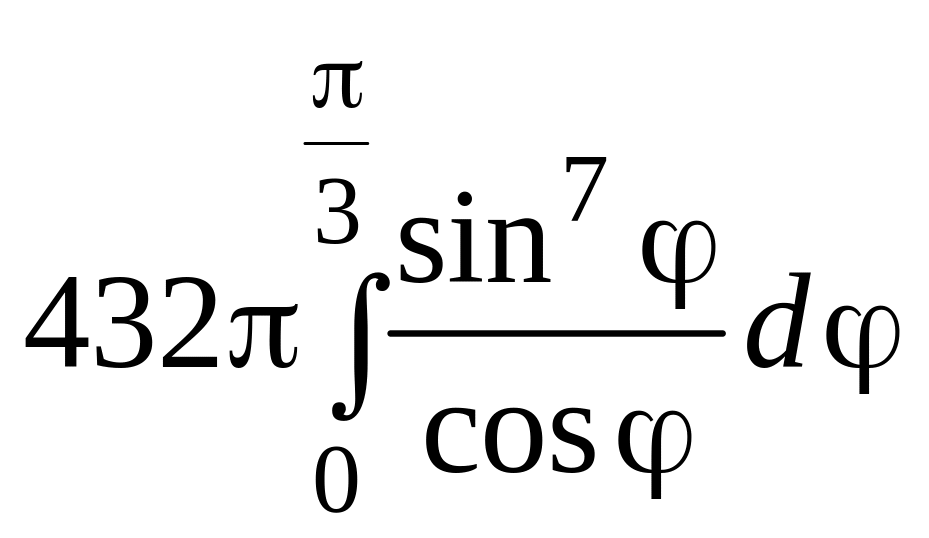Найти площадь поверхности, образованной при вращении дуги кривой.

5.52. y² = 2x, 2x = 3, вокруг оси Ox.

5.53. y = 3 c h , –1 ≤ x ≤ 1, вокруг оси Ox.

5.54. y = cos 2x, ≤ x ≤ , вокруг оси Ox.

5.55. , вокруг оси Oy.

5.56. x = , y = , 0 ≤ t ≤ π, вокруг оси Ox.

5.57. x = 2cos t – cos2 t, y = 2sin t – sin2 t, 0 ≤ t ≤ π, вокруг оси Ox.

5.58. y = (arcsin x + ), 0 ≤ x ≤ 1, вокруг оси Oy.

5.59. r = , вокруг полярной оси.

Решение.

5.52. Достаточно рассмотреть поверхность, образованную вращением кривой y = , 0 ≤ x ≤ 3/2, вокруг оси Ox. Имеем

S = = = =

= = .

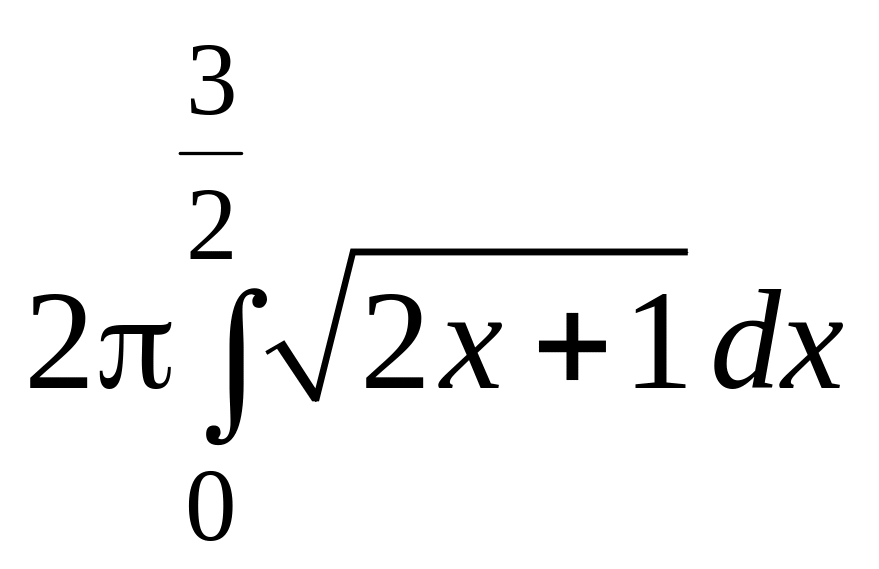5.53.

S = = = =

= = +6 .

5

Рис. 2.25

.54.

S = =

=

= = =

= = .

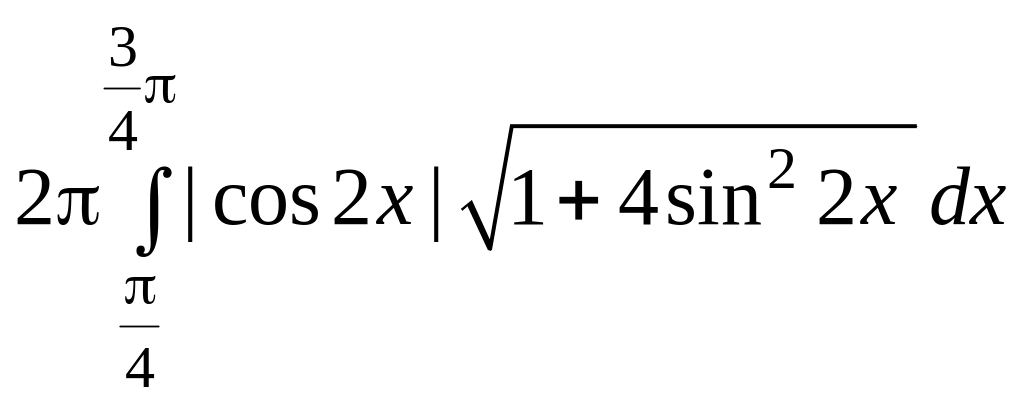5.55. Используем формулу

S = .

Имеем

Используя результаты задачи 3.6 из гл. 1, § 3, получаем

5.56.

y =

при изменении t от 0 до , при этом x возрастает от 0 до . Когда t возрастает от до π, переменная x убывает от до 0, при этом

y = .

Таким образом, наша линия – петля, симметричная относительно оси Ox. Поэтому

= = =

= = = .

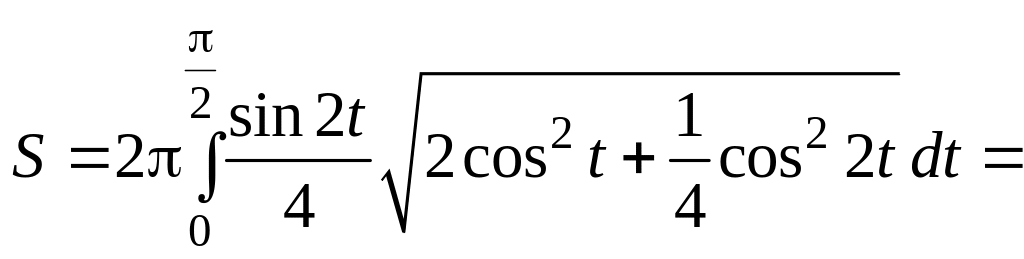
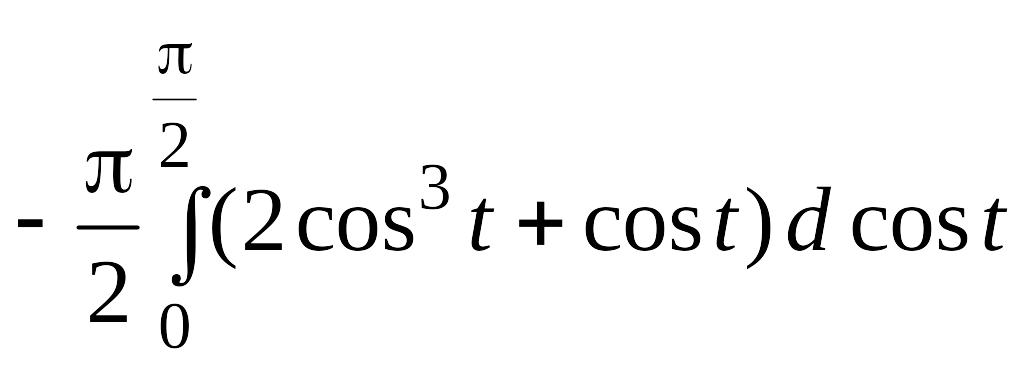5.57. Вычислим предварительно дифференциал длины дуги dl = =  .

dl = = =

= 4|sin |dt = 4 sin dt,

так как . Вычисляем площадь поверхности вращения

5.58. Выражать в данном случае x через y было бы крайне затруднительно. Поэтому параметризуем кривую, взяв за параметр x = t. Тогда

S = = =

= = = = ,

так как

= = .

5.59. Линия представляет собой два лепестка, симметричные относительно обеих осей координат Ox и Oy (x = r cos  = 3 cos  , y = r sin  = 3 sin  ). Достаточно рассмотреть дугу кривой, соответствующую изменению  от 0 до и затем удвоить результат. Вычисляем площадь поверхности вращения

S = =

= = = .