§ 5. Геометрические приложения определенных интегралов

Вычисление площадей плоских фигур. Основные формулы. Если фигура на плоскости xOy ограничена прямыми x = a, x = b (a < b) и графиками функций y = (x), y = (x), причем (x) ≤ (x) (a ≤ x ≤ b), то ее площадь вычисляется по формуле

S = .

В полярных координатах площадь сектора, ограниченного дугой кривой r = r() и лучами  =  и  =  ( ≤ ), вычисляется по формуле

.

Если граница фигуры задана параметрическими уравнениями x = x(t), y = y(t), t  (, ), то площадь фигуры вычисляется по одной из формул:

,

,

,

где  и  – значения параметра t, соответствующие началу и концу обхода контура в положительном направлении, при котором фигура остается слева.

Рассмотрим примеры.

Найти площадь фигуры, ограниченной линиями.

5.1. y = , y= . 5.2. y = tg x, y = cos x, x = 0.

5.3. y = 2x², y = . 5.4. y = ln(x + 6), y = 3 ln x, y = 0.

5.5. x = y², x = y² + 1. 5.6. y = 2^x–3 + 1, y = 2^3-x + 1, y = .

Решение.

5.1. Найдем точки пересечения графиков функций (рис. 2.1):

Рис. 2.1

= , x² + 3x – 4 = 0,

x₁ = – 4, x₂ = 1.

Вычисляем площадь

=

= =

= = .

5.2. Найдем точку пересечения графиков функций (рис. 2.2).

С

Рис. 2.2

делаем замену неизвестной sin x = z. Тогда 2 – 2z² = 3z, 2z² + 3z – 2 = 0. Решая уравнение, находим z₂= . Решение z = – 2 постороннее. Решаем да­лее, sin x = . Находим площадь

=

= = .

5

рис. 2.3

.3. Ищем точку пересечения графиков функций (рис. 2.3):

2x² = , x₁ = 0, x₂ = 6.

При 0 ≤ x ≤ 6 имеем ≤ ≤ 2x². Поэтому

S = =

=  = 36.

5.4. Ищем точку пересечения графиков функций (рис. 2.4):

ln(x + 6) = 3 ln x = ln x³, x + 6 = x³.

Я

Рис. 2.4

сно, что x = 2. Находим площадь фигуры:

S = + .

Интегралы вычисляем с помощью формулы интегрирования по частям. Для первого интеграла полагаем u = ln(x + 6), du = , v = x; для второго u = ln(x + + 6) – 3 ln x, du = , v = x.

Получаем

– + –

–  = ln7 – + 2ln8 – 6ln2 – ln7 –

–  = – 1 + 6 ln7 – 6 ln6 + – 2 +

+ 6 ln 8 + 1 – 6 ln 7 + 3 = + 1.

5

Рис. 2.5

.5. В этой задаче мы рассмотрим в качестве функции x, а y будет аргументом (рис. 2.5). Ищем точки пересечения графиков функций y² = y² + 1. Находим y₁ = – 2, y₂ = 2. Вычисляем площадь

= =

= = = .

При вычислении интеграла по отрезку [–2, 2] мы учли четность функции x = .

5

Рис. 2.6

.6. Здесь, как и в предыдущей задаче, удобнее считать y аргументом, а x – функцией. Тогда при вычислении площади нам потребуется только один интеграл, в то время как при вычислении площади фигуры, ограниченной графиками y₁ = = 2^x–3 + 1, y₂ = 2^3–x + 1, y₃ =  , понадобится два интеграла, что хорошо видно из рис. 2.6.

Найдем выражение x через y. Получаем x₁ = , x₂ = =  , ≤ y ≤ 2, так как точкой пересечения графиков функций x₁ = и x₂ = = будет точка (3, 2).

Вычисляем площадь фигуры

S = = .

Вычислим интеграл, применяя формулу интегрирования по частям, полагая

u = , du = , v = y – 1.

Тогда

S = – 2 = =

= = – 1 = .

5.7. Найти площадь фигуры (рис. 2.7), ограниченной параболой y = – x² – 2x + 3, касательной к ней в точке М(2, – 5), и осью ординат.

Решение. Найдем уравнение касательной: y = – 2x– 2, y(2) = – 6. Тогда y + 5 = – 6(x – 2) – уравнение касательной, проходящей через точку М(2, – 5). Перепишем уравнение в виде y = – 6x + 7.

В

Рис. 2.7

ычислим площадь фигуры:

S = =

= = =

= = .

Вычислить площади криволинейных трапеций, образованных графиками следующих функций.

5.8. y = , x  [0, 1).

5.9. y = х⁴e^–x, x  [0, ).

Решение.

5.8. При x[0,1) ≥ 0 и, следовательно,

S = = = =

= = + = 2.

Отметим, что в этом примере площадь вычислена с помощью несобственного интеграла.

5.9. Имеем

.

Вычислим интеграл с помощью формулы интегрирования по частям, примененной несколько раз. Воспользуемся обобщенной формулой интегрирования по частям (см. гл. I, § 3). Положим u = x⁴. Тогда u = 4x³, u = 12x², u = 24x, = 24. Далее v = e^-x, v₁ = = – e^–x, v₂ = = e^–x, v₃ = – e^–x, v₄ = e^–x.

Получим

S = = – – –

–  + .

Поскольку , m = 1, 2, … (это доказывается последовательным применением правила Лопиталя), то мы получаем

S = = = 24.

Найти площадь фигуры, ограниченной кривыми, заданными в следующих полярных координатах.

5.10. r = a cos3, (a = 2).

5.11. r = 2 – cos , r = cos .

5.12. r = , r = (внутри окружности).

5.13. r = 2,  = 0 (0 ≤  ≤ 2π).

5.14. r² = 4 cos 2, r² = 4 sin 2 (пересечение областей, ограниченных этими кривыми).

Решение.

5.10. Так как функция r = a cos 3 имеет период T = , то при изменении  от 0 до 2π радиус-вектор описывает три равных лепестка кривой (рис. 2.8). Допустимыми для  являются те значения, при которых cos 3 ≥ 0, откуда

Рис. 2.8

≤  ≤ ,

k = 0, ±1, ±2, …

При k = 0 имеем первый лепесток, соответствующий – ≤  ≤ . При k = 1 получаем пределы для , соответствующие второму лепестку, ≤  ≤ . Если k = 2, то третий лепесток линии соответствует изменениям  : ≤  ≤ . В этих трех промежутках заключена кривая, соответствующая изменению  от 0 до 2π (полный оборот). Если брать k = 3, 4, … , то мы не получим новой линии, а будем каждый раз проходить одну и ту же линию.

Поскольку лепестки одинаковы, то достаточно найти площадь одного из них и затем утроить.

Имеем

S = = 3a² = =

=  = .

При вычислении интеграла мы учли четность функции cos²3 .

5

Рис. 2.9

.11. r = cos – это уравнение окружности в полярных координатах (рис. 2.9). Найдем площадь фигуры между линией r = 2 – cos  и окружностью. Ясно, что площадь фигуры есть разность площадей, ограниченных двумя линиями:

S = S₁ – S₂, где S₁ = ,

S₂ = .

Вычисляем эти интегралы.

S₁ = =

= = ,

S₂ = = = = .

Окончательно получаем S = = .

При вычислении S₂ мы использовали четность функции cos² .

5.12. Найдем все значения , при которых cos 2 ≥ 0. Имеем

≤  ≤ , k = 0, ±1, ±2,…

П

Рис. 2.10

ри k = 0 получаем ≤  ≤ , при k = 1 : ≤  ≤ . Далее при k = 2, 3, … мы будем получать один из этих двух лепестков (рис. 2.10). Итак, фигура ограничена двумя одинаковыми лепестками. Нас интересует площадь фигуры внутри окружности r = .

Найдем полярные координаты точек пересечения кривой r =  с окружностью r = . Решая уравнение =  , получаем  = ± , k = 0, ±1, …

Выберем значения  из отрезка [–π, π] такие, что cos 2 ≥ 0. Ясно, что достаточно рассмотреть = , = , что соответствует первому лепестку. Вычислим соответствующую площадь и удвоим ее, что даст нам искомую площадь. Имеем

S = + = + = +

= + 4 – 2 .

П

Рис. 2.11

ри вычислении второго интеграла мы учли симметрию фигуры относительно полярной оси.

5.13. Линия r = 2 – спираль, раскручивающаяся из начала координат O. Нам требуется определить площадь, ограниченную одним витком спирали и полярной осью.

Вычисляем площадь.

S = = = .

5

Рис. 2.12

.14. Линия r² = 4 cos 2 представляет собой два одинаковых лепестка (рис. 2.12). Одному из них соответствуют углы ≤  ≤ , другому ≤  ≤ . Линия r² = 4 sin 2 образует два равных лепестка, один вписан в угол 0 ≤  ≤ , второй – в угол π ≤  ≤ . Найдем точки пересечения линий:

4 sin 2 = 4 cos 2, = , = .

Луч делит часть нашей области в первом квадранте пополам, луч делает то же самое с частью области в третьем квадранте. Достаточно найти площадь общей части

0 ≤ r ≤ , ≤  ≤

и умножить на четыре. Это и будет искомое решение. Вычисляем

S = = = 4 =

= = 2(2 – ).

Перейдя к полярным координатам, найти площадь области, ограниченной кривыми (рис. 2.13 и 2.14).

Рис. 2.13 Рис. 2.14

5.15. x² + y² = 6x, x² + y² = 6y, точка принадлежит области.

5.16. x² + y² = 9, x² + y² = 2 x, x + y = 0, x – y = 0,

x > 0, x² + y² ≤ 9.

Решение.

5.15. Линии являются окружностями (x – 3)² + y² = 9 и x² + (y – 3)² = 9. Пересечение кругов делится биссектрисой y = x первого квадранта на две равные половины. Найдем площадь одной, затем удвоим.

В полярных координатах x = r cos , y = r sin , уравнение x² + y² = 6x окружности принимает вид r = 6 cos , уравнение второй окружности имеет вид r = 6 sin .

Вычисляем площадь:

S = = 18 = = (π – 2).

5.16. Перейдем к полярным координатам x = r cos , y = r sin . Тогда граница области будет задаваться уравнениями r = 3, r = 2 cos ,  = – ,  = .

Наша область – фигура, симметричная относительно полярной оси (оси Ox). Найдем площадь заштрихованной области и результат удвоим. Получим искомый ответ.

Полярные координаты точки пересечения окружностей находятся из уравнения

3 = 2 cos , cos  = ,  = ± .

Вычисляем площадь:

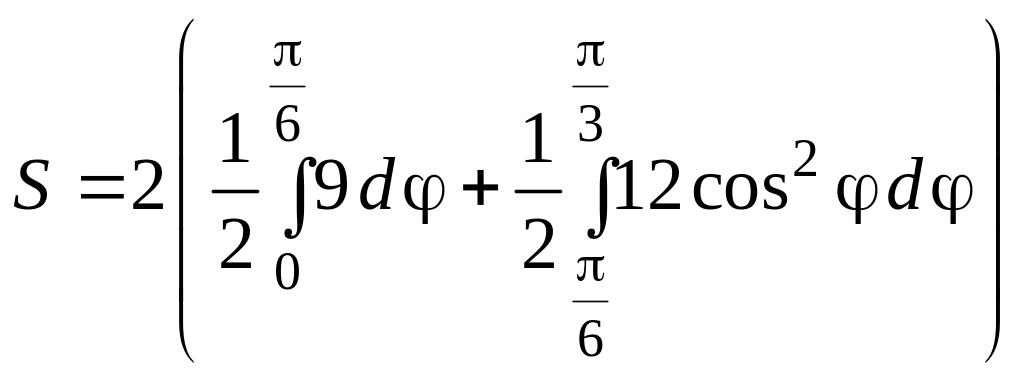= π + 6 =

= π + π + 3 = + 3 – 3 = .

Найти площадь фигуры, ограниченной кривой, заданной параметрически.

5.17. x = a cos t, y = b sin t.

5.18. x = 3 cos t, y = 3 sin 2t.

Решение.

5.17. Данная линия есть эллипс + = 1. Используя формулу для вычисления площади, находим

= =

=  = π ab.

5.18. Выражая y через x, получаем

y = ± 2x .

П

Рис. 2.15

ри x ≥ 0 и y = 2x ≥ 0.

Таким образом, при изменении t от 0 до π точка (x, y) описывает на плоскости xOy замкнутую кривую, симметричную относительно оси Ox. При изменении t от π до 2π x изменяется сначала от 0 до –3 (t изменяется от π до ), затем от –3 до 0 . Ордината y = –2x ≥ 0 при t  и y = 2x ≤ 0 – при t  , т. е. при изменении t от π до 2π мы получаем снова замкнутую кривую, симметричную первой кривой относительно оси ординат.

Мы найдем площадь фигуры, соответствующей изменению t от 0 до , а затем умножим результат на четыре. Это и даст нам искомый ответ. Вычисляем

S = = = =

= = = 24.