Признаки сходимости
Признак сравнения.
Если функции f(x)
и g(x)
удовлетворяют на полуинтервале [a,
b)
неравенству 0 ≤
f(x)
≤ g(x)
и интегрируемы на любом отрезке [a,
η], a
< η < b,
то: а) из сходимости интеграла
следует сходимость интеграла
;
б) из расходимости интеграла
вытекает расходимость интеграла
.
Предельный признак сравнения. Если g(x) > 0 на [a, b), f и g интегрируемы на [a, η] для всех a < η < b и существует
= ,
причем 0, , то интегралы и сходятся или расходятся одновременно.
Если функция f(x) незнакопостоянна на промежутке [a, b), то кроме сходимости несобственного интеграла рассматривают еще и абсолютную сходимость интеграла.
Несобственный интеграл
называется абсолютно сходящимся, если сходится интеграл
.
Абсолютно сходящийся интеграл сходится. Обратное верно не всегда. Сходящийся несобственный интеграл, расходящийся абсолютно, называется условно сходящимся.
Для исследования на сходимость интегралов от незнакопостоянных функций часто применяются признаки Абеля и Дирихле.
Признак Абеля. Пусть функции f(x) и g(x) определены на промежутке [a, b) и интегрируемы на любом отрезке [a, η] при a < η < b. Несобственный интеграл
сходится, если выполняются условия:
а) интеграл сходится;
б) функция g(x) монотонна на [a, b) и ограничена, т.е. |g(x)| ≤ M при x [a, b), где M – постоянная.
Признак Дирихле. Пусть функции f(x) и g(x) определены на [a, b) и интегрируемы на [a, η] для всех η (a, b). Тогда несобственный интеграл
сходится, если выполняются условия:
а) функция F(η)
=
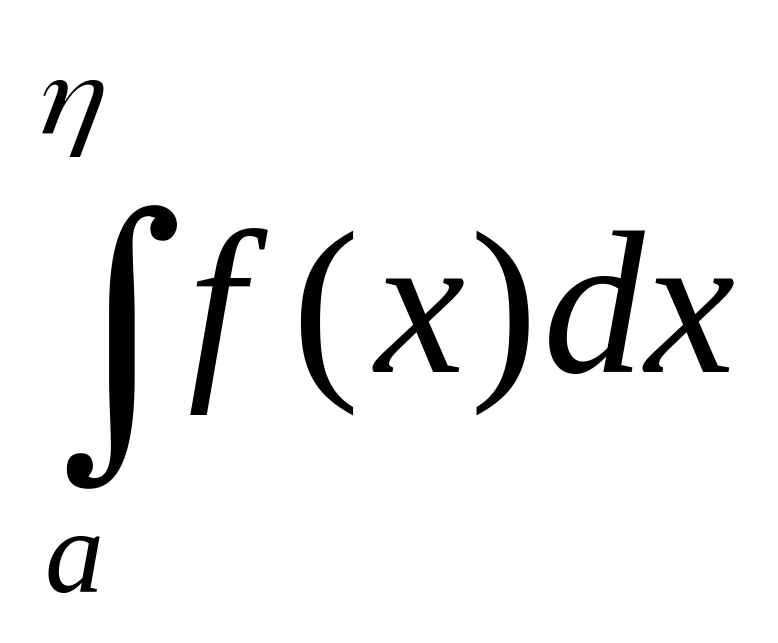ограничена на [a,
b),
т.е.
| F(η)|
=
≤ L,
где L – постоянная, η (a, b);
б) функция g(x) ограничена, монотонна на [a, b) и
=
0.
Замечание. Аналогично рассматривается случай, когда особой точкой является x = a. Для этого случая все признаки переформулируются с очевидными изменениями.
Рассмотрим примеры.
Исследовать на сходимость следующие интегралы.
3.6.
. 3.7.
.
3.8.
.
3.9.
. 3.10.
.
Решение.
3.6.
Применим признак Абеля. Интеграл
сходится (см. задачу 3.1), функция g(x)
= cos x
на [0, π]
монотонна и ограничена. По признаку
Абеля интеграл сходится.
3.7. Так как
f(x)
=
=
≤
=
g(x),
то по признаку сравнения интеграл сходится. Сходимость интеграла от g(x) = следует из задачи 3.1.
3.8. Подынтегральная функция имеет особую точку в нуле, так как не определена там. Поэтому запишем интеграл в виде суммы
=
+
.
Второй интеграл
рассмотрен в задаче 2.19. Рассмотрим
первый. Так как
=
1, то, положив
f(x)=
мы получаем непрерывную на [0,1] функцию. Так как непрерывная на отрезке функция интегрируема в обычном (собственном) смысле, то первый интеграл существует и, следовательно, наш интеграл сходится.
3.9. Применим предельный признак сравнения. Рассмотрим
f(x)
=
и g(x)
=
.
Вычисляем предел
=
=
=
= 1.
Следовательно,
наш интеграл может сходиться только
вместе с интегралом
.
Но этот интеграл расходится, значит, и
наш интеграл расходится.
3.10. Применим признак Дирихле. Перепишем подынтегральную функцию в виде
и положим
f(x)
=
,
g(x)
= 1 – x.
Имеем
=
=
=
=
= cos1 –
.
Отсюда следует
≤ 2, 0 < η < 1,
и так как g(x)
= 1 – x
монотонна на [0,1] и
=
0, то по признаку Дирихле наш интеграл
сходится.