Задачи для самостоятельного решения

Исследовать на сходимость следующие интегралы.

2.24. . 2.25. . 2.26. .

2.27. 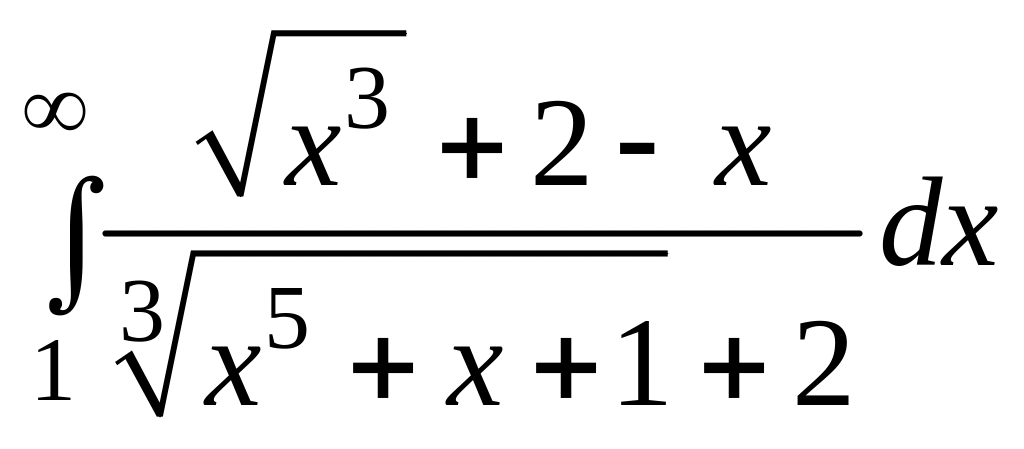. 2.28. . 2.29. .

2.30. . 2.31. . 2.32. .

§ 3. Несобственные интегралы от неограниченных функций

Пусть функция f(x) определена на полуинтервале [a, b), интегрируема на любом отрезке [a, η] [a, b) и . Если существует

,

то этот предел называется несобственным интегралом функции f(x) на промежутке [a,b) и обозначается

.

В этом случае говорят также, что несобственный интеграл сходится, а функция f(x) интегрируема в несобственном смысле по полуинтервалу [a, b). Если предел не существует, то говорят, что интеграл расходится.

Аналогично определяется несобственный интеграл функции f(x) на промежутке (a, b]:

= .

Пусть c(a, b) и функция f(x) в окрестности точки c не ограничена и пусть для любых ζ  (a, c), η  (c, b) функция f(x) интегрируема на отрезках [a, ζ] и [η, b]. Тогда несобственным интегралом f(x) на отрезке [a, b] называется сумма

= + ,

где справа стоит сумма двух несобственных интегралов:

= , = .

Если существуют оба предела, то несобственный интеграл сходится, если не существует хотя бы один предел, то расходится.

Если функция f(x) имеет на отрезке [a,b] несколько особых точек: a < c₁ < c₂ < … < c_k < b, то несобственным интегралом f(x) на [a, b] называют сумму несобственных интегралов:

= + +…+ .

Если расходится хотя бы один из интегралов в сумме, то расходится и интеграл .

Основные формулы

Линейность интеграла. Если несобственные интегралы и сходятся, то для любых постоянных C₁ и C₂ сходится интеграл , причем

= C₁ + C₂ .

Формула Ньютона–Лейбница. Если функция f(x) непрерывна на [a, b) и F(x), x[a, b), – какая-либо ее первообразная, то

= = F(b – 0) – F(a),

где F(b – 0) = .

Формула замены переменной. Пусть функция f(x) непрерывна на [a, b), а функция x =  (t), t[, ), непрерывно дифференцируема, причем

a =  () ≤  (t) <  (t) = b,

тогда

= .

Если функция x =  (t) убывает на (, ], причем

a =  () ≤  (t)< = b,

то

= .

Формула интегрирования по частям. Если u(x) и v(x) – непрерывно дифференцируемые функции на [a, b) и существует

,

то

= – ,

где

= .

Приведенные формулы справедливы и для случая, когда особая точка – левый конец промежутка x = a и функции определены на (a, b].

Рассмотрим примеры.

Вычислить интегралы или установить их расходимость.

3.1. . 3.2. . 3.3. .

3.4. . 3.5. .

Решение.

3.1. Если  = 1, то

= = ln1 – = .

Если   1, то

= = – .

При  > 1 предел бесконечный, значит, в этом случае интеграл расходится. При  < 1

= = 0,

следовательно, интеграл сходится только при  < 1 и в этом случае

= .

3.2. Сделаем замену переменной x – a = t, dx = dt, a0, bb – a. Тогда

= = , p < 1.

При остальных p интеграл расходится.

Аналогично рассматривается интеграл

,

который сходится только при p < 1. Здесь надо сделать замену b – x = t и использовать задачу 3.1.

3.3. Применим формулу интегрирования по частям:

= = – = ln1 – – = –1,

так как = 0, что устанавливается с помощью правила Лопиталя.

3.4. Вычислим интеграл, сделав замену переменной:

= = = =

= = = .

3.5. Если сделать замену переменной 4 + x = t², dx = 2t dt, –1 , 2 , то мы получим интеграл

= = ,

в то время как интеграл не существует. Действительно, особой точкой для подынтегральной функции является x = 0. Поэтому необходимо было представить наш интеграл в виде суммы

= +

и исследовать на сходимость каждый интеграл. Рассмотрим второй интеграл в сумме:

= = = =

= – = .

Следовательно, наш интеграл расходится.