Расчет зубчатых передач редуктора.

Расчёт цилиндрической косозубой передачи.

1. Определим главный параметр – межосевое расстояние , мм:

где - вспомогательный коэффициент, =43; - коэффициент ширины венца колеса, ; - передаточное число передачи; - вращающий момент на тихоходном валу ; - коэффициент неравномерности нагрузки по длине зуба. - для прирабатывающихся зубьев, -допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение .

мм.

Полученное значение округлим до ближайших значений из ряда нормальных линейных размеров [см. 1. табл. 13.15], мм.

2. Определим модуль зацепления , :

где - вспомогательный коэффициент ; мм - делительный диаметр колеса; - ширина венца колеса,

-допускаемое напряжение изгиба материала колеса с менее прочным зубом, .

Полученное значение округлим в большую сторону до стандартного из ряда чисел [см.1.табл.13.15].

мм.

3. Определяем угол наклона зуба:

4. Определим суммарное число зубьев шестерни и колеса:

П олученное число округляем до целого.

5. Уточняем угол наклона зубьев:

6. Определим число зубьев шестерни:

Полученное число округляем до z₁=31

7. Определим число зубьев колеса:

8. Определим фактическое передаточное число и проверить его отклонение от заданного :

9. Определим фактическое межосевое расстояние:

,

мм

10. Определим основные геометрические параметры передачи,

а) Делительный диаметр шестерни: мм;

б) Делительный диаметр колеса: мм;

в) Диаметр вершин зубьев колеса:

мм;

г) Диаметр вершин зубьев шестерни:

мм;

д) Диаметр впадин зубьев шестерни:

мм;

е) Диаметр впадин зубьев колеса:

мм;

ж) Ширина венца шестерни: мм;

Значения ширины зубчатых венцов округлим до целого числа по нормальным линейным размерам [см. 1 табл.13.15]. b₁=28 мм, b₂=25 мм.

Проверочный расчет.

11. Проверим межосевое расстояние: мм

12. Проверим контактные напряжения :

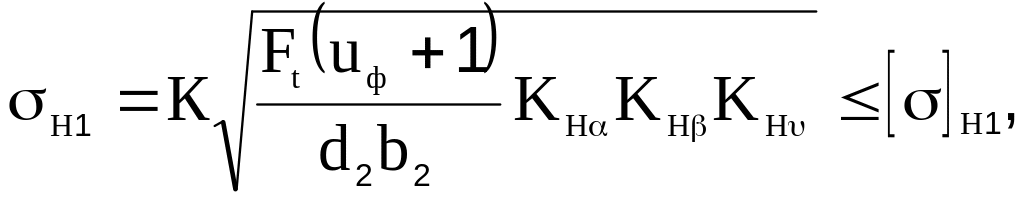
где - вспомогательный коэффициент. ; Н- окружная сила в зацеплении,

Н

- коэффициент, учитывающий распределение нагрузки между зубьями, ; - коэффициент динамической нагрузки, зависящий от окружной скорости м/с колес и степени точности передачи (см. 1. табл.4.3). , по 8 степени точности

Допускаемая перегрузка составляет не более 5%.

13. Проверим напряжения изгиба зубьев шестерни и колеса :

где - модуль зацепления; - ширина зубчатого венца колеса, - окружная сила в зацеплении, - коэффициент учитывающий распределение нагрузки между зубьями. , - коэффициент неравномерности нагрузки по длине зуба, , для прирабатывающихся колес, -коэффициент динамической нагрузки, зависящий от окружной скорости колес и от степени точности передачи [см. 1 табл.4.3] - по 9 степени точности, и - коэффициенты формы зуба шестерни и колеса.(см. 1 табл.4.4) ; , - коэффициент, учитывающий наклон зуба. , и - допускаемые значения изгиба колеса и шестерни

Н/мм²

Н/мм²

При проверочном расчете значительно меньше , это допускается, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью.

Расчёт цилиндрической шевронной передачи.

1. Определим главный параметр – межосевое расстояние , мм:

где - вспомогательный коэффициент, =43; - коэффициент ширины венца колеса, ; - передаточное число передачи; - вращающий момент на тихоходном валу ; - коэффициент неравномерности нагрузки по длине зуба. - для прирабатывающихся зубьев, -допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение .

мм

Полученное значение округлим до ближайших значений из ряда нормальных линейных размеров [см. 1. табл. 13.15], мм.

2. Определим модуль зацепления , :

где - вспомогательный коэффициент ; мм - делительный диаметр колеса; - ширина венца колеса,

мм

-допускаемое напряжение изгиба материала колеса с менее прочным зубом, .

Полученное значение округлим в большую сторону до стандартного из ряда чисел [см.1.табл.13.15].

3. Определяем угол наклона зуба:

4. Определим суммарное число зубьев шестерни и колеса:

П олученное число округляем до целого.

5. Уточняем угол наклона зубьев:

6. Определим число зубьев шестерни:

Полученное число округляем до z₃=31

7. Определим число зубьев колеса:

8. Определим фактическое передаточное число и проверить его отклонение от заданного :

9. Определим фактическое межосевое расстояние:

,

мм

10. Определим основные геометрические параметры передачи,

а) Делительный диаметр шестерни: мм;

б) Делительный диаметр колеса: мм;

в) Диаметр вершин зубьев колеса:

мм;

г) Диаметр вершин зубьев шестерни:

мм;

д) Диаметр впадин зубьев шестерни:

мм;

е) Диаметр впадин зубьев колеса:

мм;

ж) Ширина венца шестерни: мм.

Значения ширины зубчатых венцов округлим до целого числа по нормальным линейным размерам [см. 1 табл.13.15]. b₃=42 мм , b₄=40 мм.

Проверочный расчет.

11. Проверим межосевое расстояние: мм

12. Проверим контактные напряжения :

где - вспомогательный коэффициент. ; - окружная сила в зацеплении,

Н

- коэффициент, учитывающий распределение нагрузки между зубьями, ,05 ; - коэффициент динамической нагрузки, зависящий от окружной скорости м/с колес и степени точности передачи [см. 1. табл.4.3]. , по 9 степени точности

Допускаемая перегрузка передачи составляет не более 5%.

13. Проверим напряжения изгиба зубьев шестерни и колеса :

где - модуль зацепления; - ширина зубчатого венца колеса, - окружная сила в зацеплении, - коэффициент учитывающий распределение нагрузки между зубьями. , - коэффициент неравномерности нагрузки по длине зуба, , для прирабатывающихся колес, -коэффициент динамической нагрузки, зависящий от окружной скорости колес и от степени точности передачи [см. 1 табл.4.3] - по 9 степени точности, и - коэффициенты формы зуба шестерни и колеса.[см. 1 табл.4.4] ; , - коэффициент, учитывающий наклон зуба. , и - допускаемые значения изгиба колеса и шестерни

Н/мм²

Н/мм²

При проверочном расчете значительно меньше , это допускается, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью.