Контрольная работа №6.
Кратные, криволинейные, поверхностные интегралы. Элементы теории поля.
Задача 1: С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями. Сделать рисунок к задаче.
1.1.
1.2.
1.3.
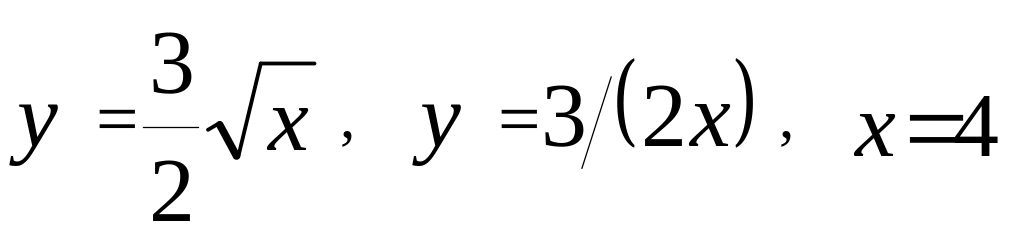
1.4.
1.5.
1.6.
1.7.
1.8.
1.9.
1.10.
1.11.
1.12.
1.13.
1.14.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
Задача 2: С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями. Сделать рисунок к задаче.
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
2.11.
2.12.
2.13.
2.14.
2.15.
2.16.
2.17.
2.18.
2.19.
2.20.
Задача 3: Вычислить криволинейный интеграл вдоль L. Сделать чертеж к задаче.
3.1.
,
где L
– дуга параболы y=2x2+4x+3,
заключенная между точками А(-2;3) и В(0;3);
3.2.
,
где L
– дуга параболы y=x2-2x-3,
заключенная между точками А(0;-3) и В(3;0);
3.3.
,
где L
– дуга параболы x=y2,
заключенная между точками А(1;1) и В(4;-2);
3.4.
,
где L
– отрезок прямой, соединяющей точки
А(1;2) и В(3;6);
3.5.
,
где L
– отрезок прямой, соединяющей точки
А(0;0) и В(3;4);
3.6.
,
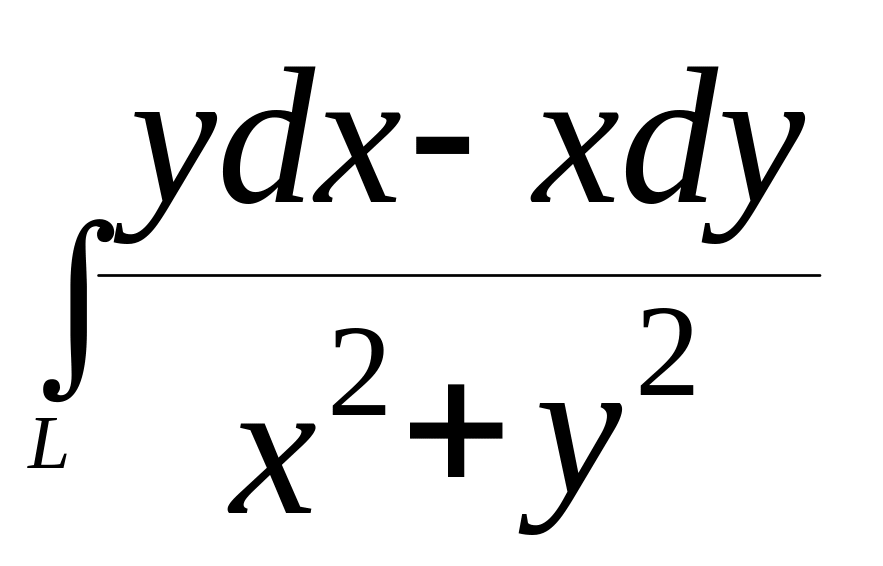где L
– окружность
,
пробегаемая по ходу часовой стрелки;
3.7.
,
где L
– отрезок прямой, соединяющей точки
А(1;2) и В(2;4);
3.8.
,
где L
– дуга параболы y2=x
от точки А(1;1) до точки В(4;2);
3.9.
,
где L
– есть треугольник с вершинами в точках
О(0;0), А(1;0) и В(0;1), пробегаемыми против
хода часовой стрелки;
3.10.
,
где L
– верхняя половина эллипса,
,
,
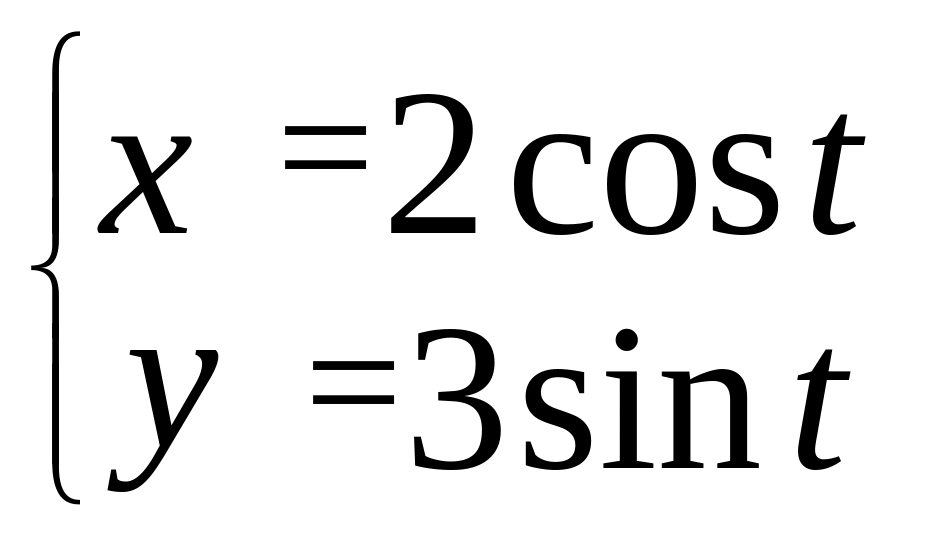пробегаемая против часовой стрелки;
3.11.
,
где L
– дуга параболы y=2x2,
заключенная между точками А(0;0) и В(1;2);
3.12.
,
где L
– дуга кривой y=ln(x)
от точки А(1;0) до точки В(e;1);
3.13.
,
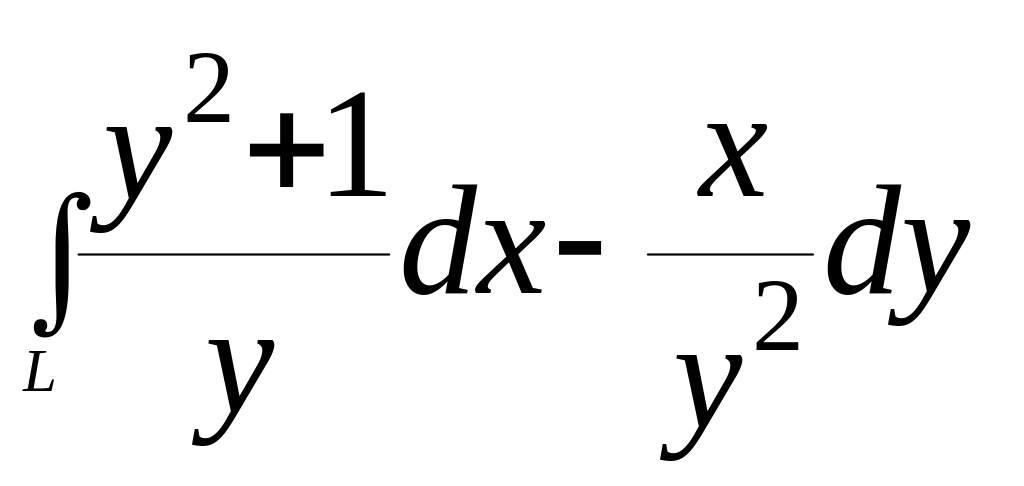где L=АВ
– отрезок прямой от точки А(1;2) до точки
В(2;4);
3.14.
,
где L
– дуга параболы y=x2
от точки А(-1;1) до точки В(1;1);
3.15.
,
где L
– ломанная, соединяющая точки
А(1;2),В(1;5) и С(3;5);
3.16.
,
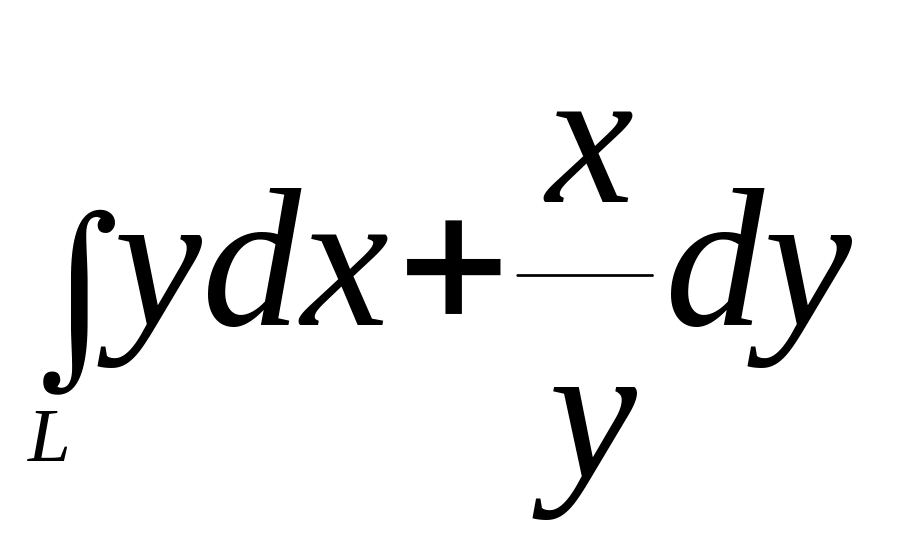где L
– дуга кривой y=e-x
от точки А(0;1) до точки
В(-1;e);
3.17.
,
где L
– верхняя половина эллипса,
,
,
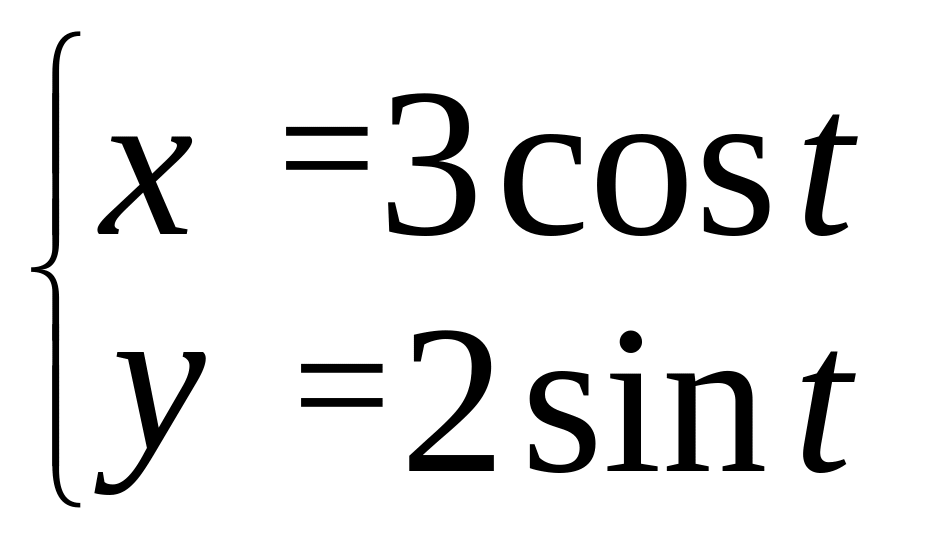пробегаемая против часовой стрелки;
3.18.
,
где L
– дуга окружности
,
от точки А(5;0) до точки В(0;5);
3.19. , где L – граница треугольника АВС, пробегаемая против хода часовой стрелки, А(1;0), В(1;1), С(0;1);
3.20.
,
где L
– ломанная ОАВ, где 0(0;0), А(2;0), В(4;5);
Задача
4: Вычислить
поток векторного поля
через внешнюю поверхность пирамиды,
образуемой плоскостью (р) совместно с
координатными плоскостями, используя
формулу Остроградского-Гаусса. Сделать
чертеж к задаче.
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
4.7.
4.8.
4.9.
4.10.
4.11.
4.12.
4.13.
4.14.
4.15.
4.16.
4.17.
4.18.
4.19.
4.20.
Задача 5: Проверить, является ли векторное поле потенциальным, соленоидальным и гармоническим. В случае потенциальности поля найти его потенциал.
5.1.
5.2.
5.3.
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10.
5.11.
5.12.
5.13.
5.14.
5.15.
5.16.
5.17.
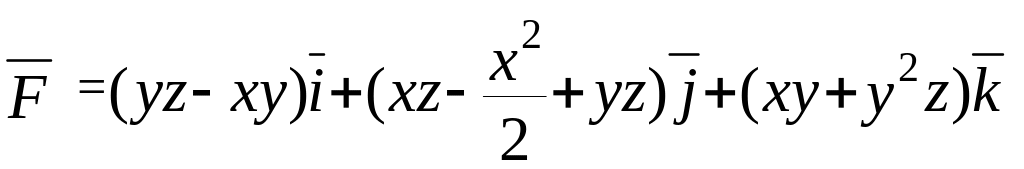
5.18.
5.19.
5.20.
