Способы задания отношений

Существуют три основных способа задания отношений:

• матрицей,

• графом,

• сечениями.

Матричный способ. Общее правило задания матрицы отношения формулируется так:

,

где , если выполнено ,

, если не выполнено .

Задание графом Элементы конечного множества  – вершины графа. От элемента к элементу проводится дуга тогда и только тогда, когда выполнено (при i = j дуга ( ) превращается в петлю при вершине ).

Задание сечениями. Этот способ менее распространён, чем предыдущие, однако он пригоден и для задания отношений на бесконечных множествах.

Определение 2

Верхним сечением называется множество элементов таких, что ; . (1.11) Аналогично определяется нижнее сечение: . (1.12)

Таким образом, множество – это множество всех элементов , с которыми фиксированный элемент находится в отношении .

Множество – это множество всех элементов , которые находятся в отношении с фиксированным элементом

Определение 3

Отношение называется дополнением отношения , если оно выполняется для тех и только тех пар, для которых не выполняется отношение . Очевидно, что \

Опреде-ление 4

Отношение Парето ( Р ) определяется следующим образом: (1.13) где множество – n-мерное пространство .

На рис 1.1 изображены верхнее и нижнее сечения отношения Р в точке

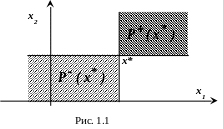
Определение 5

Множеством Парето на называется множество: . (1.14)

Из определения множества следует, что содержит те и только те элементы х^* для которых .

Пример 1.2

Пусть ;

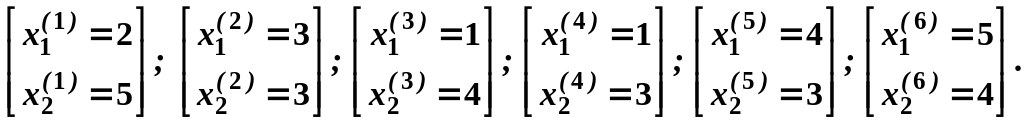
М 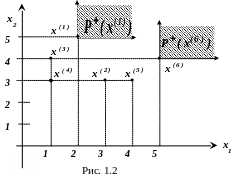ножества и изображены на рис. 1.2.

Легко видеть, что

, ,

,

,

, .

Таким образом, множество Парето включает только точки и .

Переходя к многокритериальному пространству , где и множеству решений х  Х,

где х^Т = [ х₁ , х₂ , ... , х _j , .,. х_n ], отношение Парето в соответствии с определением 4 представляет собой следующее отношение доминирования:

(1.15)

О пределение 6

Если для некоторой точки не существует более предпочтительной по Парето точки, т.е. такой точки х, что , тогда называется эффективным или Парето-оптимальным решением многокритериальной задачи: .

Множество, включающее в себя все эффективные элементы х множества , называется множеством Парето и обозначается .

Отображение множества в пространстве критериев обозначается и называется множеством эффективных оценок. Смысл введённого понятия состоит в том, что оптимальный исход следует искать среди элементов множества недоминируемых элементов ) (принцип Парето).В противном случае всегда найдётся точка , оказывающаяся более предпочтительной с учётом всех частных целевых функций

Заметим, что принцип Парето не выделяет единственного решения, он только сужает множество альтернатив, окончательный выбор остаётся за ЛПР на основе дополнительной информации о его предпочтениях.