1.4.1. Выделение главного критерия

Предположим, что введена некоторая система показателей относительно которых должен удовлетворять ограничениям:

(1.2)

Среди показателей выделим некоторый основной Тогда переходим к однокритериальной задаче:

(1.3)

при ограничениях (1.2), где .

Такая схема редукции многокритериальной задачи к однокритериальной является, вероятно, самой простой и наиболее употребительной в практике. При этом следует заметить следующее [32]:

1. Переход от исходной задачи (1.1) к задаче (1.3) не есть переход от одной эквивалентной задачи к другой.

2. Не всегда ясен алгоритм определения границ

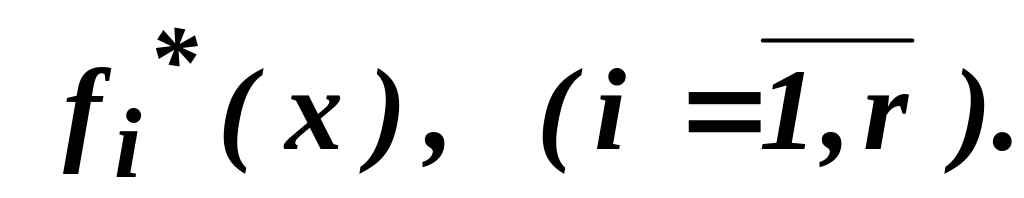
3. Возможно наличие нескольких «главных» критериев, находящихся в противоречии друг с другом.

1.4.2. Методы формирования свёртки критериев

В случае использования аддитивных преобразований свёртка выглядит следующим образом:

(1.4)

где b _i ( x ) – коэффициент важности соответствующего критерия

Аддитивное преобразование для построения единого критерия очень часто используется, если объединение различных частных критериев проводится на экономической основе.

В случае использования мультипликативной свёртки обобщённый критерий формируется следующим образом:

(1.5)

где – некоторые вещественные числа.

Использование преобразования (1.5) характерно для тех задач принятия решений, где частными критериями являются некоторые вероятностные характеристики или где возможно использование в качестве некоторых удельных характеристик.

Например, обобщённый критерий технико-экономической эффективности ЭВМ, предложенный в [36], построен следующим образом:

(1.6)

где и отражает эффективное быстродействие ЭВМ, причём является критерием оценки технической эффективности ЭВМ и зависит от её важнейших технических характеристик (системы операций, номинального быстродействия, ёмкости памяти, надёжности, скорости работы устройств ввода-вывода);

– суммарные затраты на изготовление, амортизацию и эксплуатацию ЭВМ за время Т;

– объём работы, выполненной ЭВМ за время её живучести, в пересчёте на число операций типового набора;

Т – время живучести ЭВМ.

Если критерии измеряются в различных шкалах, то необходимо привести их к единой шкале. Для этого обычно формируют следующий критерий:

(1.7)

где

К недостаткам данного метода можно отнести существование возможных неоднозначных компенсаций значений критериев.

1.4.3. Введение метрики в пространстве целевых функций

Предположим, что решена система однокритериальных задач:

(1.8)

Совокупность скалярных величин определяет в пространстве критериев некоторую точку, которую назовём точкой «абсолютного максимума». Если найденные векторы х^* в каждой из задач (1.8) различны, то не существует такого выбора, который позволил бы достичь этой точки. Точка является недостижимой в пространстве критериев.

Введём метрику в виде эвклидова расстояния от точки

до точки

в пространстве критериев:

(1.9)

В качестве нового скалярного критерия можно принять функцию (1.9). Её минимизация даёт исследователю определённую полезную информацию и показывает предельные возможности достижения абсолютного максимума.