
- •1.Введение
- •1.1 Задачи и методы сопротивления материалов.
- •1.2 Классификация сил, действующих на элементы конструкций.
- •1.3 Основные предпосылки науки о сопротивлении материалов.
- •1.4 Реальный объект и расчетная схема.
- •1.5 Внутренние силы. Метод сечений.
- •1.6 Напряжения.
- •1.7 Деформации и перемещения.
- •1.8 План решения основной задачи сопротивления материалов.
- •2. Растяжение и сжатие
- •2.1 Продольная сила
- •2.2 Вычисление напряжений по площадкам, перпендикулярным и наклонным к оси стержня.
- •2.3 Допускаемые напряжения. Подбор сечений.
- •2.4 Продольные и поперечные деформации
- •2.5 Диаграммы растяжения и сжатия
- •2.6 Основные механические характеристики материала
- •2.7 Работа силы при ее статическом действии. Потенциальная энергия деформации
- •2.9 Перемещения поперечных сечений брусьев
- •2.10 Допускаемые напряжения. Расчеты на прочность.
- •2.11 Статически неопределимые системы
- •3.Сложное напряжённое состояние.
- •3.1Виды напряженного состояния.
- •3.2Напряжения по наклонным сечениям при осевом растяжении или сжатии (линейное напряжённое состояние).
- •3.3Понятие о главных напряжениях. Виды напряжённого состояния материала.
- •3.4Напряжения при плоском напряжённом состоянии.
- •3.5 Графическое определение напряжений (круг Мора).
- •3.6 Нахождение наибольших напряжений для объёмного напряжённого состояния.
- •3.8 Понятие о теориях прочности.
- •3.9 Проверка прочности по различным теориям.
- •4.1 Понятие о сдвиге. Расчёт заклепок на перерезывание.
- •4.2 Проверка заклёпок на смятие и листов на разрыв.
- •4.3 Расчёт сварных соединений.
- •4.4 Чистый сдвиг. Определение главных напряжений и проверка прочности.
- •4.5 Связь между напряжениями и деформацией при чистом сдвиге. Потенциальная энергия сдвига.
- •5.1 Основные понятия. Крутящий момент.
- •5.2 Определение напряжений при кручении круглого вала.
- •5.3 Вычисление полярных моментов инерции и моментов сопротивления сечения вала.
- •5.4 Условие прочности при кручении.
- •5.5 Определение деформаций при кручении.
- •5.6 Потенциальная энергия при кручении.
- •5.7 Определение предельной грузоподъёмности скручиваемого стержня.
- •6.8 Напряжения и деформации в винтовых пружинах с малым шагом.
- •5.9 Статически неопределимые задачи при кручении
- •6. Изгиб
- •§ 6.1. Внутренние силовые факторы, возникающие в поперечных сечениях бруса при изгибе
- •§ 6.2. Напряжения в брусе при чистом изгибе
- •§ 6.3. Напряжения при поперечном изгибе
- •§ 6.4. Дифференциальное уравнение упругой линии балки. Перемещения при изгибе
- •§ 6.5. Универсальное уравнение упругой линии балки
- •§6.6 Контроль правильности построения эпюр q и m.
- •§6.7. Способ сложения действия сил при построении эпюр.
- •§6.8. Графический метод построения эпюр изгибающих моментов и поперечных сил.
- •7. Вычисление моментов инерции плоских фигур.
- •§7.1. Вычисление моментов инерции и моментов сопротивления для простейших сечений.
- •§7.2. Общий способ вычисления моментов инерции сложных сечений.
- •§ 7.3. Подбор сечения балок по допускаемым нагрузкам.
- •§7.4. Применение понятия о потенциальной энергии к определению деформаций.
- •§ 7.5. Вычисленние потенциальной энергии.
- •§7.6. Теорема Кастильяно.
- •§7.7 Статически неопределимые балки.
- •§7.8. Способ сравнения деформаций.
- •§7.9. Применение теоремы Кастильяно, теоремы Мора
- •§7.10. Выбор лишней неизвестной и основной системы.
- •§7.11. План решения статически неопределимой задачи.
- •8. Косой изгиб
- •§8.1. Основные понятия.
- •§8.2. Косой изгиб. Вычисление напряжений.
- •§8.3. Определение деформаций при косом изгибе
- •9. Совместное действие изгиба и растяжения или сжат
- •9.1 Изгиб балки при действии продольных и поперечных сил.
- •9.3. Ядро сечения
- •10.Совместное действие кручения и изгиба
- •11.3 Зависимость критической силы от условий закрепления стержня
- •12.1. Введение»
- •12.2 Вычисление напряжений при равноускоренном движении
- •12.3 Расчёт вращающегося кольца (обод маховика)
§7.2. Общий способ вычисления моментов инерции сложных сечений.
При проверке частей конструкций нам приходится встречаться с сечениями довольно сложной формы, для которых нельзя вычислять моментов инерции таким простым путем, каким мы пользовались для прямоугольника и круга.
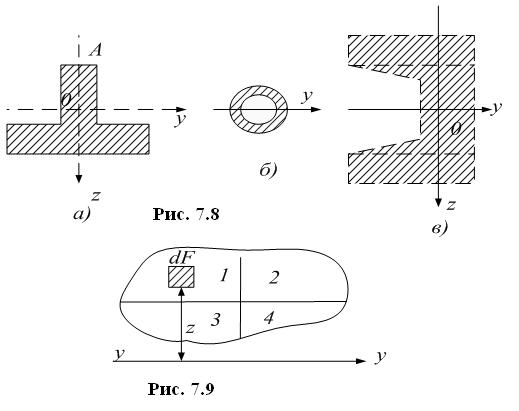
Таким сечением может быть, например, тавр (Рис. 7.8, а), кольцевое сечение трубы, работающей на изгиб (авиационные конструкции) (Рис. 7.8, б), кольцевое сечение шейки вала или ещё более сложное сечение (Рис. 7.8, в). Все эти сечения можно разбить на простейшие, как-то: прямоугольники, треугольники, круги и т.д. Можно сказать что момент инерции такой сложной фигуры является суммой моментов инерции частей, на которые мы её разбиваем.
Возьмем
(Рис. 7.9) какую угодно фигуру, изображающую
поперечное сечение балки; в её плоскости
проведена ось у – у .Момент инерции этой
фигуры относительно у-у равен:
 ,где
z
расстояние элементарных площадок dF
до оси у-у.
,где
z
расстояние элементарных площадок dF
до оси у-у.
Разобьем
взятую площадь на четыре части:
, ,
, ,
, .
.
Теперь при вычислении момента инерции можно сгруппировать слагаемые в подынтегральной функции так, чтобы отдельно произвести суммирование для каждой из выделенных четырех площадей, а затем эти суммы сложить. Величина интеграла от этого не изменится.
Наш интеграл разобьется на четыре интеграла, каждый из которых будет охватывать одну из площадей F1, F2,F3 или F4:

Каждый из интегралов представляет собой момент инерции соответствующей части площади относительно оси у – у; поэтому

где
 момент инерции относительно оси у –у
площади
,
момент инерции относительно оси у –у
площади
,
 -
то же для площади
и т д.
-
то же для площади
и т д.
Полученный результат можно формулировать так: момент инерции сложной фигуры равен сумме моментов инерции составных её частей.
Поэтому, чтобы вычислить например, момент инерции сечения, изображенного на Рис. 7.8, в, относительно оси Оу, необходимо найти моменты инерции прямоугольников и треугольников относительно оси Оу и затем сложить их. Таким образом, нам необходимо уметь вычислять момент инерции любой фигуры относительно любой оси, лежащей в её плоскости. Решение этой задачи и составляет содержание настоящей главы.
§ 7.3. Подбор сечения балок по допускаемым нагрузкам.
Все предыдущее изложение было построено на методе подбора сечения и проверки прочности балок по допускаемым напряжениям. Но уже на примере скручиваемого стержня мы видели, что при неравномерном распределении напряжений по сечению метод подбора размеров сечения по допускаемым нагрузкам даёт иной результат. Подобный же случай мы имеем и при изгибе. В методе расчета по допускаемым напряжениям мы пользовались для подбора сечения балок условием:
 .
.
Здесь для материалов, имеющих площадку текучести (мягкая сталь), было равно

Где
 -
предел текучести, а
-
предел текучести, а
 -
соответствующий коэффициент запаса.
-
соответствующий коэффициент запаса.
Таким
образом, опасным мы представляем себе
здесь то состояние, когда наибольшее
напряжение в опасном сечении балки
дойдет до предела текучести. Изгибающий
момент при этом состоянии назовем дойдет
до предела текучести. Изгибающий момент
при этом состоянии назовем дойдет до
предела текучести. Изгибающий момент
при этом состоянии назовем
 ;
он соответствует достижению грузоподъёмности
материала в наиболее напряженных
волокнах опасного сечения балки. Однако
этому состоянию не будет отвечать
исчерпание грузоподъёмности всей балки,
как конструкции.
;
он соответствует достижению грузоподъёмности
материала в наиболее напряженных
волокнах опасного сечения балки. Однако
этому состоянию не будет отвечать
исчерпание грузоподъёмности всей балки,
как конструкции.
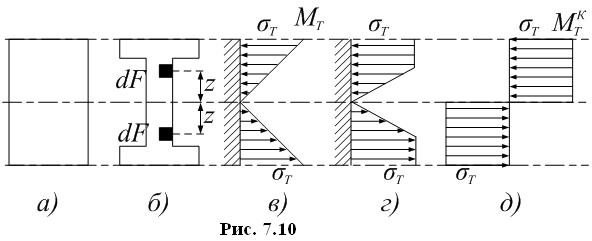
Возьмем стальную балку симметричного (например прямоугольного или двутаврового) сечения (Рис. 7.10, а и б). При моменте, равном , распределение напряжений в опасном сечении показано на Рис. 7.10, в, напряжение дошло до предела текучести лишь в крайних волокнах, вся остальная часть балки находится в упругом состоянии. Поэтому для дальнейшей деформации балки необходимо новое увеличение нагрузки и изгибающего момента: грузоподъёмность балки ещё не исчерпана.
При увеличении момента зона текучести будет распространяться внутрь балки, эпюра напряжений примет вид, показанный на Рис. 7.10, г, и в пределе, когда материал по всей высоте сечения потечёт и грузоподъемность балки будет полностью исчерпана, эпюра напряжений примет форму двух прямоугольников (Рис. 7.10, д). Изгибающий момент на этой стадии работы балки и будет предельным, разрушающим для балки в целом. Дальнейшая деформация балки пойдет еже без увеличения момента, в опасном сечении образуется так называемый пластический шарнир.
Определим
величину этого предельного момента
 .
Он будет равен сумме моментов относительно
нейтральной оси усилий по Рис. 7.10, д. На
площадку dF
на расстоянии z
от нейтральной оси будет действовать
сила
dF,
момент этой силы относительно нейтральной
оси равен
dF
*z.
По симметрии сечения достаточно вычислить
сумму моментов этих сил для верхней и
нижней половины сечения и результат
удвоить; тогда
.
Он будет равен сумме моментов относительно
нейтральной оси усилий по Рис. 7.10, д. На
площадку dF
на расстоянии z
от нейтральной оси будет действовать
сила
dF,
момент этой силы относительно нейтральной
оси равен
dF
*z.
По симметрии сечения достаточно вычислить
сумму моментов этих сил для верхней и
нижней половины сечения и результат
удвоить; тогда
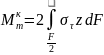 ,
,
где F-площадь всего сечения. Так как постоянно для всех точек сечения, то
 ,
,
поскольку интеграл
 ,
,
Представляет собой статический момент половины сечения относительно нейтральной оси. Условие прочности имеет вид
 ;
;
При
коэффициенте запаса
 получаем:
получаем:
 И
И
 .
.
Следовательно, при расчете по допускаемым нагрузкам вместо подбора сечения симметричной балки по её моменту сопротивления W приходится подбирать размеры по величине удвоенного статического момента полу сечения балки. Для прямоугольного сечения высотой h и шириной b.
