3.6 Нахождение наибольших напряжений для объёмного напряжённого состояния.

Для случая объёмного напряжённого состояния напряжения по любой площадке можно представить также графически.

Пусть мы имеем выделенный из тела элемент кубической формы, на грани которого действуют три главных напряжения: σ1,σ2,σ3(рис.3.15). Поставим задачу нахождения нормального и касательного напряжений по любой площадке, пересекающей выделенный кубик.

Сначала будем искать эти напряжения по площадкам, параллельным одному из главных напряжений, например σ1. На рис.3.15, а эта площадка заштрихована.

Как мы видели выше, главное напряжение, параллельное проведенной площадке, не вызывает по ней ни нормальных, ни касательных напряжений. Поэтому напряжения по рассматриваемым площадкам будут зависеть лишь от σ2 и σ3— для них мы будем иметь дело с плоским напряженным состоянием. Тогда этим площадкам будут соответствовать точки круга напряжений, построенного на главных напряжениях σ2 и σ3 (рис.3.15, б).

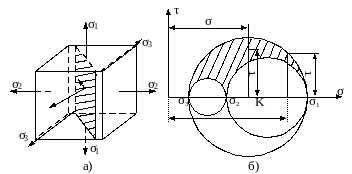
Рис.3.15

Точно так же напряжения по площадкам, направленным параллелью σ2, будут изображаться коордипатами точек круга, построепиого на напряжениях σ1 и σ3; для площадок, параллельных σ3 — на напряжениях σ1 и σ3.

Таким образом, координаты точек трёх кругов напряжения (рис.3.15, б) изображают нормальные и касательные напряжения по сечениям кубика, параллельным одному из главных напряжений.

Что же касается площадок, пересекающих все три оси главных напряжений, то в теории упругости показано, что для них на напряжения σ и 𝜏 изображаются координатами точек D заштрихованной на рис.3.15, б площади.

Значения этих напряжений могут быть вычислены по формулам:

σα=σ1cos2α1+σ2cos2α2+σ3cos2α3, (3.15)

τα=σ12cos2α1+σ22cos2α2+σ32cos2α3-σα. (3. 16)

Здесь α1, α2 и α3 — углы, составленные нормально к площадке с направлениями соответствующих главных напряжений σ1,σ2 и σ3.

Из рис.3.15 ясно, что в случае объёмного напряжённого состояния наибольшее и наименьшее нормальные напряжения равны соответственно наибольшему и наименьшему главным напряжениям.

Наибольшее касательное напряжение равно радиусу наибольшего круга, следователю, полуразности наибольшего и наименьшего главных напряжений. Оно действует по площадкам, наклоненным под углом 45° к направлению этих главных напряжений, причём нормальные напряжения на таких площадках равны полусумме наибольшего и наименьшего главных напряжений (σ1 > σ2 > σ3).

Таким образом, в общем случае напряжённого состояния материала, когда в рассматриваемой точке все три главных напряжения не равны нулю, получаем:

max σα=σ1; max σα=σ3; max τα=σ1-σ22; (3.17)

По площадкам, параллельным одному из главных напряжений и наклонённым к двум другим на угол 45°, касательные напряжения будут: max τ формуле (3.17), далее

σ1,2=σ1-σ22 ; τ2,3=σ2-σ32 (3.17')

Вычисление деформаций при плоском и объёмном напряжённом состояниях.

При проверках прочности элемента (рис.3.15), на грани которого действуют напряжения σ1,σ2 и σ3 нам придётся столкнуться с вопросом о величинах соответствующих деформаций. Называя ребро, параллельное главному напряжению σ1 первым, а рёбра, параллельные главным напряжениям σ2 и σ3 вторым и третьим, определим относительные продольные деформации элемента в направлении этих рёбер, отдельно рассматривая влияние каждого из напряжений и складывая результаты.

Под действием напряжений σ1 элемент в направлении первого ребра получит относительное удлинение, равное ε1'=σ1E.

В то же время по отношению к напряжениям σ2 и σ3 первое ребро является поперечным размером, а потому под действием напряжений σ2 и отдельно σ3 элемент в направлении первого ребра испытывает относительные ускорения, равные:

ε1''=-μσ2E; ε1'''=-μσ3E.

Полная относительная деформация элемента в направлении первого ребра выразится суммой

ε1=ε1'+ε1''+ε1'''=σ1E=-μσ2E=-μσ3E.

Если σ1=σ2=σ3=σ, то

θ=(1-2μ)E3σ.

Величину E3(1-2μ) называют модулем объёмной деформации и обозначают буквой К. Тогда, вводя это обозначение находим:

θ=ε1+ε2+ε3=σ1+σ2+σ33К.

Мы видим, что изменение объема зависит лишь от суммы главных напряжений, а не от их соотношения. Поэтому кубик получит одно и то же изменение объема, будут ли по его граням действовать различные по величине главные напряжения σ1,σ2 и σ3 или одинаковые напряжения:

σn=σ1+σ2+σ33;

В последнем случае все ребра кубика получат одинаковую деформацию:

εn=ε1+ε2+ε33=σ1+σ2+σ33К*3=σn3К .