§ 6.4. Дифференциальное уравнение упругой линии балки. Перемещения при изгибе

Форму изогнутой оси бруса или, как говорят, форму упругой линии можно определить при помощи выражения (6.5)

В неподвижной системе координат yz (рис. 6.28)

Ограничимся рассмотрением случая малых перемещений. Тогда тангенс угла 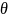между касательной к упругой линии и осью (рис. 6.28) весьма мал. Поэтому квадратом величины у' по сравнению с единицей можно пренебречь и принять

откуда

(6.14)

Рис. 6.28

Сопоставляя выражение (4.14) с формулами (4.1), получаем очевидную цепочку дифференциальных соотношений:

(6.15)

или для бруса с постоянным сечением:

(6.16)

Из этих формул видно, что в случае нагружения бруса постоянного сечения равномерно распределенной нагрузкой имеем

Следовательно, форма оси изогнутого бруса описывается кривой четвертого порядка.

Если на некотором участке бруса интенсивность , то ось бруса будет изогнута по кривой третьего порядка.

Понятно, что все написанные выше соотношения являются точными в той мере, в какой перемещения можно считать малыми. Подавляющее большинство задач, связанных с расчетами на прочность и жесткость при изгибе, решается в указанном предположении, причем с весьма высокой степенью точности, поскольку величина , отброшенная в выражении (6.13), действительно ничтожно мала.

В некоторых случаях возникает необходимость решить задачу при больших упругих перемещениях. Такого рода задачи встречаются в основном при исследовании специальных пружин приборов.

Если упругая система при больших перемещениях способна сохранять упругие свойства, то она называется гибкой, независимо от того, идет ли речь об изгибе, кручении или растяжении. При изгибе величина предельных упругих перемещений определяется не только свойствами материала, но в равной мере величиной отношения длины бруса к размеру поперечного сечения в плоскости изгиба.

Наибольшее удлинение при изгибе согласно формуле (6.2) будет

А напряжение –

Большие перемещения брус сможет получить при условии большого изменения кривизны Но в области напряжений, не превышающих предела упругости, это возможно только при достаточно малом , т.е. при малой высоте сечения. Гибкий брус имеет поэтому обычно форму тонкой ленты или тонкой проволоки и часто называется тонким гибким стержнем.

Рис. 6.28

Рис. 6.29

Дифференциальное уравнение упругой линии гибкого стержня имеет вид

Отличие этого уравнения от уравнения (6.14) заключается не только в том, что здесь сохраняется нелинейный член в знаменателе. Для гибкого стержня выражение должно составляться с обязательным учетом перемещений, возникающих в стержне, что при обычном построении эпюр моментов не делается. Указанная особенность гибких стержней наглядно иллюстрируется примером консоли (рис. 6.28). Видно, что с ростом прогибов вертикальная сила Р получает горизонтальное смещение. В результате этого изгибающий момент в каждой точке бруса изменится на некоторую величину, зависящую как от местного горизонтального смещения, так и от горизонтального смещения точки приложения силы Р.

Общие методы изучения больших перемещений бруса при изгибе объединяются так называемой теорией гибких стержней. Эта теория выходит за рамки сопротивления материалов и в настоящем курсе рассматриваться не будет.

Рассмотрим некоторые примеры определения формы упругой линии изогнутого бруса в области малых перемещений.

После двукратного интегрирования находим

где и — постоянные интегрирования, определяемые из граничных условий. В данном случае при имеем Тогда

Наибольший прогиб имеет место в точке приложения силы Р, т. е. при , и равен