5.1 Основные понятия. Крутящий момент.

Кручением называется такой вид деформации, при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор- крутящий момент Mк. Кручение возникает в валах, винтовых пружинах и других элементах конструкций. Кручение прямого бруса происходит при нагружении его внешними скручивающими моментами (парами сил), плоскости действия которых перпендикулярны в его продольной оси. Эти моменты обозначим М. Кручение криволинейных брусьев может возникать и при других видах нагружения.

Если прямой брус находится в состоянии покоя или равномерного вращения, то алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, равна нулю.

При расчете валов в ряде случаев величины внешних скручивающих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов, то угол поворота вала за 1 сек, выраженный в радианах, равен n602π, или πn30. Работа скручивающего момента за 1 сек, т.е. мощность N, передаваемая валом, равна произведению величины момента на угол поворота вала ( в радианах) за 1 сек:

N=Mπn30

Откуда

M=30Nπn кГм

Где мощность N выражена в кГм/сек.

Если мощность N задана в лошадиных силах (л.с.), то

M=30*75Nπn=716,2Nπ кГм=71620Nπ кГм (5.1)

Если мощность N задана в киловаттах, то, учитывая, что 1 л. с. равна 0,736 квт, получаем

M=973,6Nπ кГм=97360Nπ кГм (5.2)

Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются по внешним скручивающим моментам с помощью метода сечений. В простейшем случае, когда брус нагружен только двумя внешними моментами (эти моменты из условия равновесия бруса ∑Mx=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент Mк в любом поперечном сечении бруса (на участке между внешними моментами) по величине равен внешнему моменту M1=M2.

Рис. 5.1

В более сложных случаях, когда к брусу приложено кесколько внешних моментов, крутящие моменты в поперечных сечениях различных участков бруса неодинаковы.

На основании метода сечений крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.

Рис. 5.2

При расчетах па прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эпюр Mк примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2). В частности, в сечении 1 бруса, изображенного на рис. 1.6,а, крутящий момент отрицателен (рис. 5.1,б) и численно равен внешнему моменту M1 или M2.

На рис. 5.3 изображен брус, к которому приложены четыре внешних скручивающих момента. Крутящий момент M1к в сечении 1-1 численно равен M1 и, согласно принятому правилу знаков, отрнцателен. Крутящий момент в сечении 2-2 численно равен разности моментов M1 и M2, т. е.; M2к=M1-M2,а его знак зависит от соотношения этих моментов: если M2>M1, то момент M2к положителен, а если M2<M1, то отрицателен.

Рис. 5.3

Абсолютная величина крутящего момента в сечении 3-3 бруса, если его вычислять по внешним моментам, приложенным слева от рассматриваемого сечения, определится из выражения

M3к=M1-M2-M3

В данном случае крутящий момент M3к удобнее определять по внешним нагрузкам, приложенным справа от сечения 3-3,так как с этой стороны приложен лишь один внешний момент m4 (вместо трех внешних моментов, приложенных слева от сечения). Момент M3к, действующий на правую отсеченную часть бруса, направлен противоположно моменту M4, что следует из условия равновесия этой части, следовательно, по принятому правилу знаков он положителен.

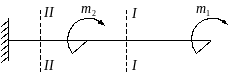
Рис.5.4

Для брусьев, имеющих один неподвижно закрепленный (заделанный) и один свободный конец, крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные с той стороны от рассматриваемого сечения, с которой расположен свободный конец. Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке. Так, например, крутящие моменты MIк и MIIк I-I и II-II бруса, изображенного на рис. 5.4,можно определить без вычисления реактивного момента левой заделки:

MIк=m1

MIIк=m1+m2

Оба момента MIк и MIIк положительны.

Изменение крутящих моментов по длине бруса удобно изображать графически — с помощью так называемой эпюры крутящих моментов. На рис. 5.5, а показана такая эпюра для бруса, изображенного на рис. 5.1,а. На рис. 5.6,в показана эпюра крутящих моментов для бруса, изображенного на рис. 5.5,б.

Каждая ордината эпюры крутящих моментов в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината. В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента (рис. 5.5,б,в).

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость. Так, например, на рис 5.6,б наибольший внешний момент равен 300 кГ см, а наибольший ( по абсолютной величине) крутящий момент (внутренний) равен 250 кГ см (рис.5.6,в)

Рис. 5.5