
- •1.Введение
- •1.1 Задачи и методы сопротивления материалов.
- •1.2 Классификация сил, действующих на элементы конструкций.
- •1.3 Основные предпосылки науки о сопротивлении материалов.
- •1.4 Реальный объект и расчетная схема.
- •1.5 Внутренние силы. Метод сечений.
- •1.6 Напряжения.
- •1.7 Деформации и перемещения.
- •1.8 План решения основной задачи сопротивления материалов.
- •2. Растяжение и сжатие
- •2.1 Продольная сила
- •2.2 Вычисление напряжений по площадкам, перпендикулярным и наклонным к оси стержня.
- •2.3 Допускаемые напряжения. Подбор сечений.
- •2.4 Продольные и поперечные деформации
- •2.5 Диаграммы растяжения и сжатия
- •2.6 Основные механические характеристики материала
- •2.7 Работа силы при ее статическом действии. Потенциальная энергия деформации
- •2.9 Перемещения поперечных сечений брусьев
- •2.10 Допускаемые напряжения. Расчеты на прочность.
- •2.11 Статически неопределимые системы
- •3.Сложное напряжённое состояние.
- •3.1Виды напряженного состояния.
- •3.2Напряжения по наклонным сечениям при осевом растяжении или сжатии (линейное напряжённое состояние).
- •3.3Понятие о главных напряжениях. Виды напряжённого состояния материала.
- •3.4Напряжения при плоском напряжённом состоянии.
- •3.5 Графическое определение напряжений (круг Мора).
- •3.6 Нахождение наибольших напряжений для объёмного напряжённого состояния.
- •3.8 Понятие о теориях прочности.
- •3.9 Проверка прочности по различным теориям.
- •4.1 Понятие о сдвиге. Расчёт заклепок на перерезывание.
- •4.2 Проверка заклёпок на смятие и листов на разрыв.
- •4.3 Расчёт сварных соединений.
- •4.4 Чистый сдвиг. Определение главных напряжений и проверка прочности.
- •4.5 Связь между напряжениями и деформацией при чистом сдвиге. Потенциальная энергия сдвига.
- •5.1 Основные понятия. Крутящий момент.
- •5.2 Определение напряжений при кручении круглого вала.
- •5.3 Вычисление полярных моментов инерции и моментов сопротивления сечения вала.
- •5.4 Условие прочности при кручении.
- •5.5 Определение деформаций при кручении.
- •5.6 Потенциальная энергия при кручении.
- •5.7 Определение предельной грузоподъёмности скручиваемого стержня.
- •6.8 Напряжения и деформации в винтовых пружинах с малым шагом.
- •5.9 Статически неопределимые задачи при кручении
- •6. Изгиб
- •§ 6.1. Внутренние силовые факторы, возникающие в поперечных сечениях бруса при изгибе
- •§ 6.2. Напряжения в брусе при чистом изгибе
- •§ 6.3. Напряжения при поперечном изгибе
- •§ 6.4. Дифференциальное уравнение упругой линии балки. Перемещения при изгибе
- •§ 6.5. Универсальное уравнение упругой линии балки
- •§6.6 Контроль правильности построения эпюр q и m.
- •§6.7. Способ сложения действия сил при построении эпюр.
- •§6.8. Графический метод построения эпюр изгибающих моментов и поперечных сил.
- •7. Вычисление моментов инерции плоских фигур.
- •§7.1. Вычисление моментов инерции и моментов сопротивления для простейших сечений.
- •§7.2. Общий способ вычисления моментов инерции сложных сечений.
- •§ 7.3. Подбор сечения балок по допускаемым нагрузкам.
- •§7.4. Применение понятия о потенциальной энергии к определению деформаций.
- •§ 7.5. Вычисленние потенциальной энергии.
- •§7.6. Теорема Кастильяно.
- •§7.7 Статически неопределимые балки.
- •§7.8. Способ сравнения деформаций.
- •§7.9. Применение теоремы Кастильяно, теоремы Мора
- •§7.10. Выбор лишней неизвестной и основной системы.
- •§7.11. План решения статически неопределимой задачи.
- •8. Косой изгиб
- •§8.1. Основные понятия.
- •§8.2. Косой изгиб. Вычисление напряжений.
- •§8.3. Определение деформаций при косом изгибе
- •9. Совместное действие изгиба и растяжения или сжат
- •9.1 Изгиб балки при действии продольных и поперечных сил.
- •9.3. Ядро сечения
- •10.Совместное действие кручения и изгиба
- •11.3 Зависимость критической силы от условий закрепления стержня
- •12.1. Введение»
- •12.2 Вычисление напряжений при равноускоренном движении
- •12.3 Расчёт вращающегося кольца (обод маховика)
2.9 Перемещения поперечных сечений брусьев
Определим
вертикальное продольное перемещение
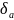 точка а
оси бруса, растянутого силой Р,
изображенного на рис. 2.17. Оно равно
абсолютной деформации части бруса ad,
заключенной между заделкой и сечением,
проведенным через точку а, т.е.
точка а
оси бруса, растянутого силой Р,
изображенного на рис. 2.17. Оно равно
абсолютной деформации части бруса ad,
заключенной между заделкой и сечением,
проведенным через точку а, т.е.
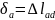 .
.

Рис. 2.17
Продольная
деформация бруса определяется по
формуле:
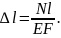 Это формула применима, лишь когда в
пределах всего участка длиной l
продольные силы N
и жесткости EF
поперечных сечений бруса постоянны. В
рассматриваемом случае на участке ab
продольная сила N
равна нулю (собственный вес бруса не
учитываем), а на участке bc
она равна Р; кроме того, площадь поперечного
сечения бруса на участке cd.
Поэтому продольную деформацию участка
ad
следует определять как сумму продольных
деформаций трех участков ab,
bc
и cd,
для каждого из которых значения N
и EF
постоянны по всей его длине:
Это формула применима, лишь когда в
пределах всего участка длиной l
продольные силы N
и жесткости EF
поперечных сечений бруса постоянны. В
рассматриваемом случае на участке ab
продольная сила N
равна нулю (собственный вес бруса не
учитываем), а на участке bc
она равна Р; кроме того, площадь поперечного
сечения бруса на участке cd.
Поэтому продольную деформацию участка
ad
следует определять как сумму продольных
деформаций трех участков ab,
bc
и cd,
для каждого из которых значения N
и EF
постоянны по всей его длине:
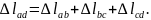
Продольные силы на рассматриваемых участках бруса
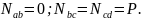
Следовательно,
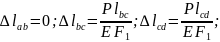
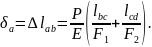
Аналогично можно определить перемещения δ любых точек оси бруса, а по их значениям построить эпюру продольных перемещений (эпюру δ), т.е. график, изображающий изменение этих перемещений по длине оси бруса.
Продольные перемещения точек оси равны продольным перемещениям проходящих через эти точки поперечных сечений бруса.
При продольной нагрузке, распределенной по длине оси бруса, продольная сила N в поперечных сечениях его непрерывно изменяется. В этих случаях, а также в случае, когда жесткость EF бруса переменна по длине его оси, для определения продольной деформации необходимо рассматривать брус, состоящий из бесчисленного множества бесконечно малых участков длиной dl. Продольная деформация каждого такого участка вызывает продольную силу N=G
Потенциальную энергию деформации бруса найдем по формуле:
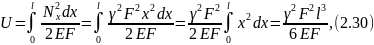
или
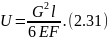
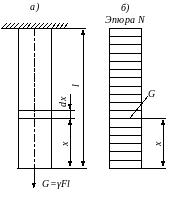
Рис. 2.18
Найдем
теперь перемещение поперечного сечения
I-I
того же бруса (рис. 2.16, г). Это сечение
перемещается вниз на величину
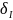 ,
равную удлинению
,
равную удлинению
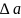 верхней части бруса длиной а.
верхней части бруса длиной а.
Удлинение
участка длиной а определяем от собственного
веса этого участка
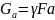 и веса
и веса
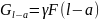 нижерасположенной части бруса длиной
l-a
(рис. 2.16, д). Деформацию от веса
нижерасположенной части бруса длиной
l-a
(рис. 2.16, д). Деформацию от веса
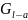 определяем по формуле (2.15), так как вес
является для участка а внешней силой,
а деформацию от веса
определяем по формуле (2.15), так как вес
является для участка а внешней силой,
а деформацию от веса
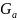 - по формуле (2.29). При этом в указанные
формулы подставляем а вместо l.
Тогда
- по формуле (2.29). При этом в указанные
формулы подставляем а вместо l.
Тогда
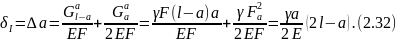
Подставляя в выражение (2.32) различные значения а, можно получить величины вертикальных (продольных) перемещений δ различных поперечных сечений рассматриваемого бруса и построить по ним эпюру продольных перемещений (эпюру δ), изображенную на рис. 2.16, е.
2.10 Допускаемые напряжения. Расчеты на прочность.
Основной задачей расчета конструкции является обеспечение ее прочности в условиях эксплуатации.
Прочность конструкции, выполненной из хрупкого металла, считается обеспеченной, если во всех поперечных сечениях всех ее элементов фактические напряжения меньше предела прочности материала. Величины нагрузок, напряжения в конструкции и предел прочности материала нельзя установить совершенно точно (в связи с приближенностью методики расчета, способов определения предела прочности и т.д.). Поэтому необходимо, чтобы наибольшие напряжения, полученные в результате расчета конструкции (расчетные напряжения), не превышали некоторой величины, меньшей предела прочности, называемой допускаемым напряжением. Значение допускаемого напряжения устанавливается путем деления предела прочности на величину, большую единицы, называемую коэффициентом запаса. В соответствии с изложенным условие прочности конструкции, выполненной из хрупкого материала, выражается в виде
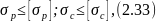
где
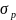 и
и
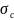 - наибольшие расчетные растягивающие
и сжимающие напряжения в конструкции;
- наибольшие расчетные растягивающие
и сжимающие напряжения в конструкции;
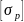 и
и
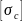 – допускаемые напряжения при растяжении
и сжатии соответственно.
– допускаемые напряжения при растяжении
и сжатии соответственно.
Допускаемые напряжения и зависят от пределов прочности материала на растяжение и сжатие и определяются выражениями
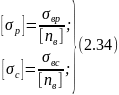
где
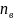 - нормативный (требуемый) коэффициент
запаса прочности по отношению к пределу
прочности.
- нормативный (требуемый) коэффициент
запаса прочности по отношению к пределу
прочности.
В
формулы (2.33) и (2.34) подставляются абсолютные
значения напряжений
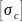 ,
,
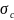 и
.
и
.
Для конструкций из пластичных материалов (у которых пределы прочности на растяжение и сжатие одинаковы) используется следующее условие прочности:
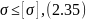
где
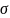 - наибольшее по абсолютной величине
сжимающее или растягивающее расчетное
напряжение в конструкции.
- наибольшее по абсолютной величине
сжимающее или растягивающее расчетное
напряжение в конструкции.
Допускаемое
напряжение
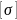 для пластичных материалов определяется
по формуле
для пластичных материалов определяется
по формуле
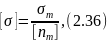
где
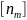 - нормативный (требуемый) коэффициент
запаса прочности по отношению к пределу
текучести.
- нормативный (требуемый) коэффициент
запаса прочности по отношению к пределу
текучести.
Использование при определении допускаемых напряжений для пластичных материалов предела текучести (а не предела прочности, как для хрупких материалов) связано с тем, что после достижения предела текучести деформации могут весьма резко увеличиваться даже при незначительном увеличении нагрузки и конструкции могут перестать удовлетворять условиям их эксплуатации.
Расчет прочности, выполняемый с использованием условий прочности (2.33) или (2.35), называется расчетом по допускаемым напряжениям. Нагрузка, при которой наибольшие напряжения в конструкции равны допускаемым напряжениям, называется допускаемой нагрузкой.
Следует стремиться к тому, чтобы допускаемые напряжения были полностью использованы, т.е. чтобы удовлетворялось условие σ=[ σ]; если это по ряду причин (например, в связи с необходимостью стандартизации размеров элементов конструкции) не удается, то расчетные напряжения должны как можно меньше отличаться от допускаемых. Возможно незначительное превышение расчетных допускаемых напряжений и, следовательно, некоторое снижение фактического коэффициента запаса прочности (по сравнению с нормативным).
Расчет центрально растянутого или сжатого элемента конструкции на прочность должен обеспечить выполнение условия прочности для всех поперечных сечений элемента. При этом большое значение имеет правильное определение так называемых опасных сечений элемента, в которых возникают наибольшие растягивающие и наибольшие сжимающие напряжения. В тех случаях, когда допускаемые напряжения на растяжение или сжатие одинаковы, достаточно найти одно опасное сечение, в котором имеются наибольшие по абсолютной величине нормальные напряжения.
При постоянной по длине бруса, величине продольной силы, опасным является поперечное сечение, площадь которого имеет наименьшее значение. При брусе постоянного сечения опасным является то поперечное сечение, в котором возникает наибольшая продольная сила.
При расчете конструкций на прочность встречаются три вида задач, различающихся формой использования условий прочности:
а) проверка напряжений (проверочный расчет);
б) подбор сечений (проектный расчет);
в) определение грузоподъемности (определение допускаемой нагрузки). Рассмотрим эти виды задач на примере растянутого стержня из пластичного материала.
а) При проверке напряжений площади поперечных сечений F и продольные силы N известны и расчет заключается в вычислении рабочих (фактических) напряжений σ в характерных сечениях элементов. Полученные при этом наибольшие напряжения сравнивают затем с допускаемым:
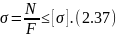
б) При подборе сечении определяют требуемые площади [F] поперечных сечений элемента (по известным продольным силам N и допускаемому напряжению [σ]). Принимаемые площади сечений F должны удовлетворять условию прочности, выраженному в следующем виде:
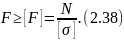
в) При определении грузоподъемности по известным значениям F и допускаемому напряжению [σ] вычисляют допускаемые величины [N] продольных сил: [N]=F[σ]. По полученным значениям [N] затем определяются допускаемые величины внешних нагрузок [P].
Для этого случая условие прочности имеет вид
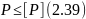
Величины нормативных коэффициентов запаса прочности устанавливаются нормами. Они зависят от класса конструкции (капитальная, временная и т.п.), намечаемого срока ее эксплуатации, нагрузки (статическая, циклическая и т.п.), возможной неоднородности изготовления материалов (например, бетона), от вида деформации (растяжение, сжатие и т.д.) и других факторов.
В ряде случаев приходится снижать коэффициент запаса в целях уменьшения веса конструкции, а иногда увеличивать коэффициент запаса- при необходимости учитывать износ трущихся частей машин, коррозию и загнивание материала.
Величины
нормативных коэффициентов запаса для
различных
материалов, сооружений и нагрузок имеют
в большинстве случаев значения:
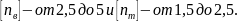
Коэффициенты запаса прочности, а следователю, и допускаемые напряжения для строительных конструкций регламентированы соответствующими нормами их проектирования. В машиностроении - обычно конструктор выбирает требуемый коэффициент запаса прочности, ориентируясь на опыт проектирования и эксплуатации машин аналогичных конструкций. Кроме того, ряд передовых машиностроительных заводов имеет внутризаводские нормы допускаемых напряжений, часто используемые и другими родственными предприятиями.
