Метод Крамера
Пусть имеется система уравнений 3-го порядка
,
(8)
где,
применительно к рассматриваемым примерам
,
,
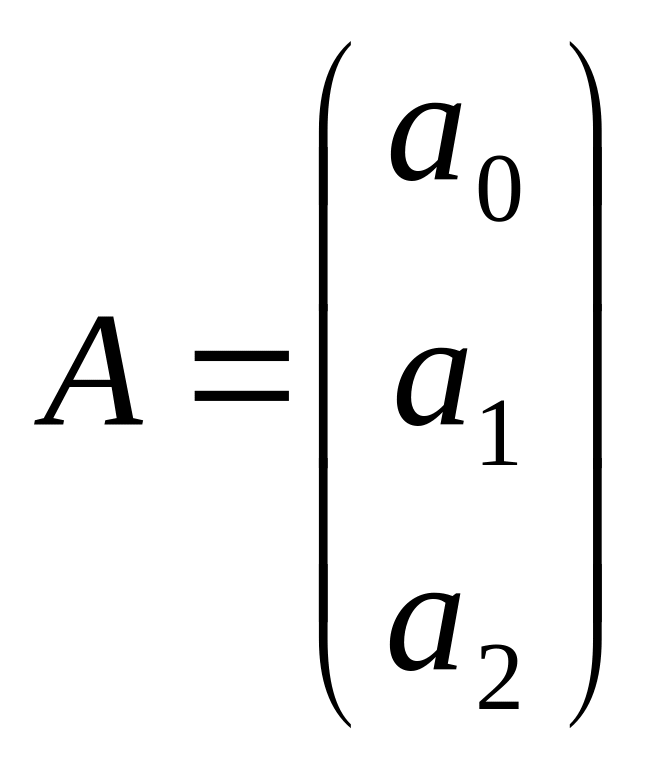
или в матричном виде
СA=Y
где C – матрица коэффициентов системы; A – вектор неизвестных; Y – вектор правых частей.
Согласно теореме Крамера решение может быть найдено из формулы:
,
(9)
где Ci – матрица C у которой i-й столбец заменен вектором свободных членов – вектором Y.
Т.е.
Найдем определители матриц С, С0,С1, С2.
,
,
.
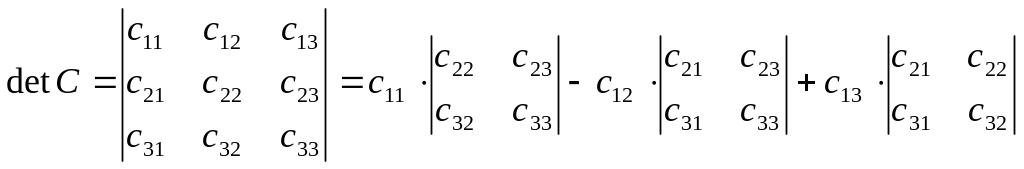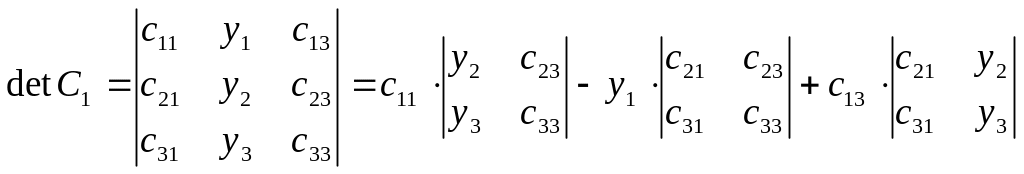Найдем a0, a1, a2.
,
,
.
Метод Гаусса
В основе метода Гаусса используются элементарные преобразования матрицы коэффициентов системы с целью приведения ее к более простому виду (например, треугольному) решение которой не представляет труда. В качестве таких преобразований используются:
а) вычитание из одной строки другой, умноженной на константу, отличную от нуля;
б) перестановка строк;
в) умножение строки на число отличное от нуля.
Пусть имеется система линейных уравнений 3-го порядка:
,
и матрица коэффициентов системы не имеет нулевых диагональных элементов и ее определитель отличен от нуля. Тогда решение может быть получено следующим образом.
Разделим все элементы первой строки на с11 (включая y):
Исключим элементы первого столбца из второго и третьего уравнений системы (элементы c21 и c31). Для этого элементы первой строки умножим на c21 и c31, т.е. получим:
и
Затем из элементов второй и третьей строки вычтем соответствующие элементы полученных уравнений, т.е.
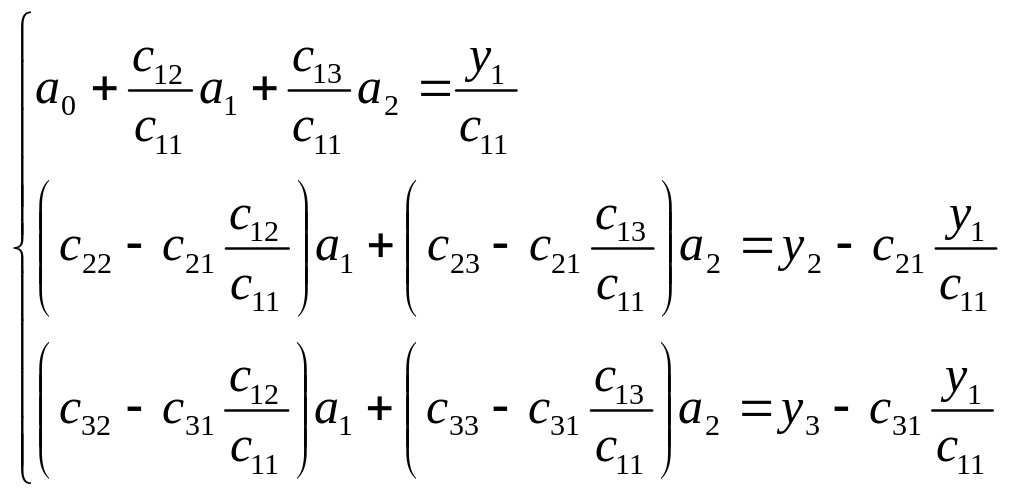или
где
,
,
,
,
,
,
,
,
.
Вновь
полученную вторую строку, разделим на
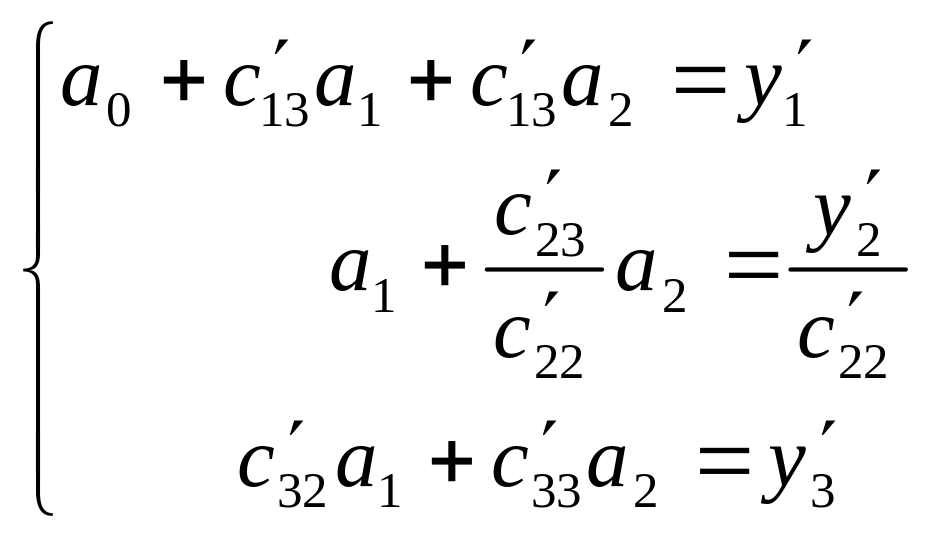
Исключим элемент
из третьей строки. Для этого элементы
второй строки умножим на
Затем из элементов третьей строки вычтем элементы полученного уравнения.
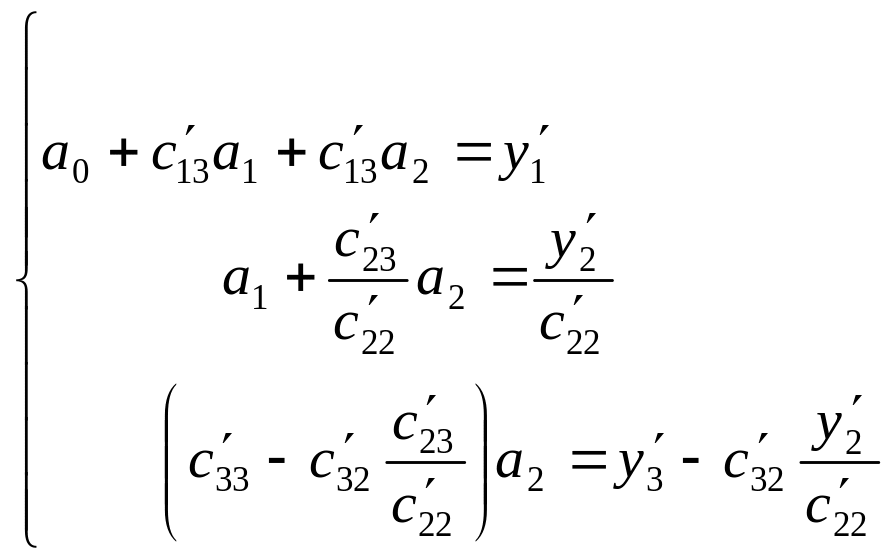или
где
,
,
,
Из последнего уравнения находим a2, из второго a1 и из первого – a0.
Метод обращения матриц
Пусть имеется система линейных уравнений СA=Y
Если это уравнение умножить слева и справа на обратную матрицу C-1
C-1 CA = C-1Y, то учитывая, что C-1 C =Е получим A= C-1Y. E – единичная матрица.
Сложность этого метода заключается в нахождении с-1, которая рассчитывается следующим образом. Находится ст, т.Е., если
,
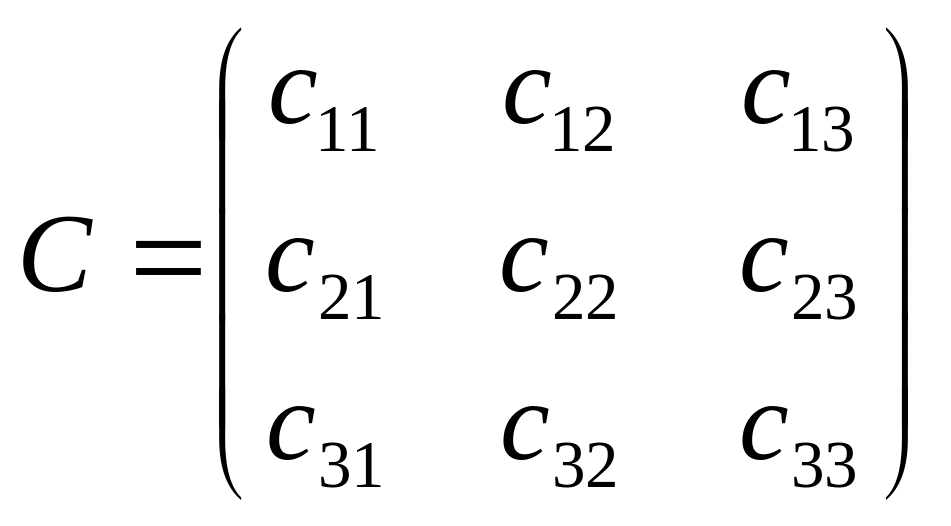то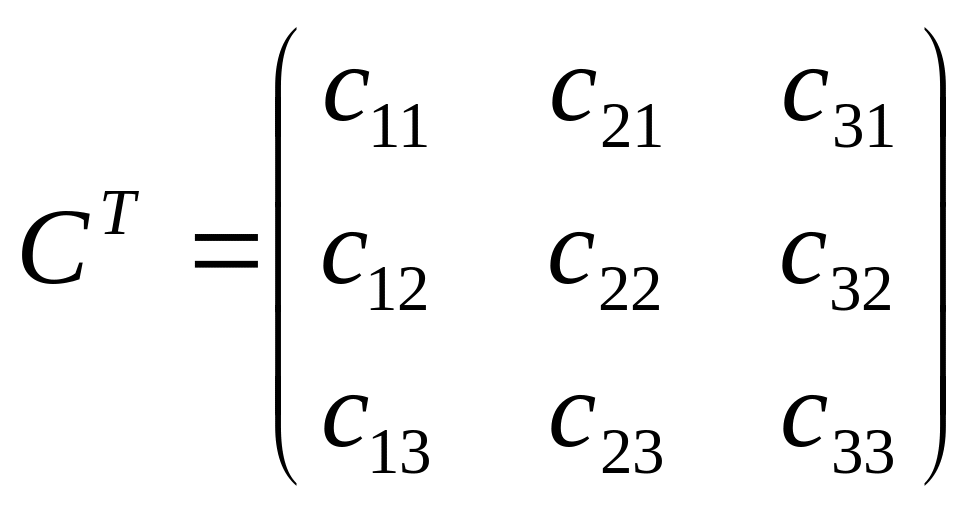
.
Затем рассчитывается матрица алгебраических дополнений:
,
где
С i,j
– алгебраические дополнения элементов
С i,j
(
),
которые находятся следующим образом
,
,
,
,
,
,
,
,
.
Знак “-” ставится перед определителем в том случае, если сумма индексов определителя является нечетным числом.
ПРИЛОЖЕНИЕ 2
Номер варианта |
Табличные зависимости
|
Контрольная температура |
Метод решения системы линейных уравнений |
|||
i |
1 |
2 |
3 |
|||
1.1 |
ti,С Ri,Oм |
32 85. |
70 92 |
100 98 |
38 |
Гаусса |
1.2 |
ti,С Ri,Oм |
5 50 |
45 56.1 |
85 63.5 |
55.5
|
Обращения матриц |
1.3 |
ti,С Ri,Oм |
5 100 |
25 105. |
45 111 |
25 |
Крамера |
1.4 |
ti,С Ri,Oм |
5 80 |
35 103 |
75 112.3 |
72 |
Обращения матриц |
1.5 |
ti,С Ri,Oм |
40 111 |
60 117 |
80 126 |
63 |
Гаусса |
1.6 |
ti,С Ri,Oм |
5 50 |
45 61 |
85 69.1 |
68 |
Обращения матриц |
1.7 |
ti,С Ri,Oм |
5 80 |
32 88 |
70 99.5 |
16 |
Крамера |
1.8 |
ti,С Ri,Oм |
5 100 |
25 113 |
45 123 |
28 |
Гаусса |
1.9 |
ti,С Ri,Oм |
20 106 |
60 116 |
100 142.5 |
88 |
Крамера |
1.10 |
ti,С Ri,Oм |
5 50 |
35 56.1 |
75 63.5 |
23 |
Обращения матриц |
1.11 |
ti,С Ri,Oм |
5 111 |
45 117 |
85 126 |
43 |
Гаусса |
1.12 |
ti,С Ri,Oм |
2 50 |
25 61. |
45 99.1 |
34 |
Крамера |
1.13 |
ti,С Ri,Oм |
40 100 |
60 113 |
80 123 |
74 |
Крамера |
Окончание прил. 2
Номер варианта
|
Табличные зависимости
|
Контрольная температура |
Метод решения системы линейных уравнений |
|||
i |
1 |
2 |
3 |
|||
2.1 |
ti,С Ri,Oм |
22 45. |
70 92 |
100 98 |
28 |
Крамера |
2.2 |
ti,С Ri,Oм |
25 52 |
55 56.1 |
85 62.5 |
55.5
|
Обращения матриц |
2.3 |
ti,С Ri,Oм |
4 1. |
14 10. |
24 101 |
5 |
Гаусса |
2.4 |
ti,С Ri,Oм |
5 88 |
32 103 |
70 110. |
16 |
Обращения матриц |
2.5 |
ti,С Ri,Oм |
40 113 |
60 115 |
80 126 |
63 |
Гаусса |
2.6 |
ti,С Ri,Oм |
5 50 |
25 61 |
85 69.1 |
68 |
Крамера |
2.7 |
ti,С Ri,Oм |
5 10 |
30 88 |
70 99.5 |
16 |
Обращения матриц |
2.8 |
ti,С Ri,Oм |
15 100 |
35 103 |
55 113 |
28 |
Гаусса |
2.9 |
ti,С Ri,Oм |
22 100 |
64 116 |
100 122.5 |
80 |
Крамера |
2.10 |
ti,С Ri,Oм |
5 10 |
35 46.1 |
65 53.5 |
23 |
Обращения матриц |
2.11 |
ti,С Ri,Oм |
25 11 |
65 14 |
105 106 |
40 |
Крамера
|
2.12 |
ti,С Ri,Oм |
2 5 |
25 6. |
45 9.1 |
7 |
Гаусса
|
2.13 |
ti,С Ri,Oм |
40 1 |
60 10 |
80 13 |
7 |
Крамера |
ПРИЛОЖЕНИЕ 3
Номер варианта |
Вещество |
Табличные зависимости |
Заданная температура |
Метод интерполирования |
||||||
I |
1 |
2 |
3 |
4 |
5 |
6 |
||||
1.1 |
Глицерин (50 %-ный) |
ti,С , кг/м3 |
0 1136 |
20 1126 |
40 1116 |
60 1102 |
80 1090 |
-
|
24 |
1-я интерполяционная формула Ньютона |
1.2 |
NaOH (50 %-ный) |
ti,С , кг/м3 |
0 1540 |
20 1525 |
60 1497 |
80 1483 |
120 1454 |
- |
36 |
Полином Лагранжа |
1.3 |
Сероугле-род |
ti,С , кг/м3 |
-20 1323 |
20 1263 |
60 1200 |
100 1125 |
- |
- |
53 |
2-я интерполяционная формула Ньютона |
1.4 |
NaOH (30 %-ный) |
ti,С , кг/м3 |
20 1328 |
40 1316 |
60 1303 |
80 1289 |
100 1276 |
- |
63 |
1-я интерполяционная формула Ньютона |
1.5 |
Толуол |
ti,С , кг/м3 |
0 884 |
20 866 |
40 847 |
60 828 |
80 808 |
- |
42 |
2-я интерполяционная формула Ньютона |
1.6 |
Фенол |
ti,С , кг/м3 |
20 1075 |
40 1058 |
60 1040 |
80 1022 |
100 1003 |
- |
63 |
2-я интерполяционная формула Ньютона |
1.7 |
Олеум (20 %-ный) |
ti,С , кг/м3 |
0 1922 |
40 1870 |
60 1844 |
100 1792 |
- |
- |
61 |
Полином Лагранжа |
1.8 |
NaOH (10 %-ный) |
ti,С , кг/м3 |
0 1117 |
40 1100 |
80 1077 |
120 1049 |
- |
- |
73 |
2-я интерполяционная формула Ньютона |
1.9 |
Аммиак жидкий |
ti,С , кг/м3 |
-20 665 |
0 639 |
20 610 |
40 580 |
- |
- |
14 |
1-я интерполяционная формула Ньютона |
1.10 |
Двуокись серы |
ti,С , кг/м3 |
0 1434 |
20 1383 |
40 1327 |
60 1264 |
80 1193 |
100 1111 |
26 |
1-я интерполяционная формула Ньютона |
1.11 |
Бутиловый спирт |
ti,С , кг/м3 |
-20 838 |
0 824 |
20 810 |
40 795 |
60 781 |
100 751 |
42 |
Полином Лагранжа |
1.12 |
NaOH (20 %-ный) |
ti,С , кг/м3 |
0 1230 |
20 1219 |
60 1196 |
80 1183 |
120 1155 |
- |
73 |
Полином Лагранжа |
1.13 |
NaOH (40 %-ный) |
ti,С , кг/м3 |
0 1443 |
20 1430 |
40 1416 |
60 1403 |
80 1389 |
100 1375 |
15 |
2-я интерполяционная формула Ньютона |