2.3. Предварительные понятия:

• Средняя длина свободного пробега

• Эффективный диаметр молекулы

Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Термин «столкновение» применительно к молекулам не следует понимать буквально и представлять себе этот процесс подобным соударению твердых шаров. Под столкновением молекул подразумевают процесс взаимодействия между молекулами, в результате которого молекулы изменяют направление своего движения.

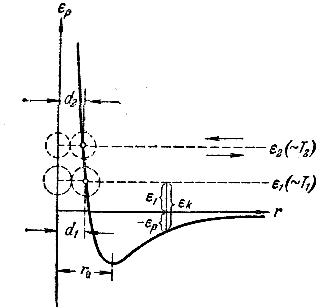
На рис.1 показана кривая, изображающая взаимную потенциальную энергию двух молекул как функцию расстояния r между их центрами.

Рассмотрим с помощью этой кривой процесс сближения (соударения) молекул.

• Поместим мысленно центр одной из молекул в начало координат, а центр второй молекулы представим перемещающимся по оси r.

• Пусть вторая молекула летит по направлению к первой из бесконечности, имея начальный запас кинетической энергии .

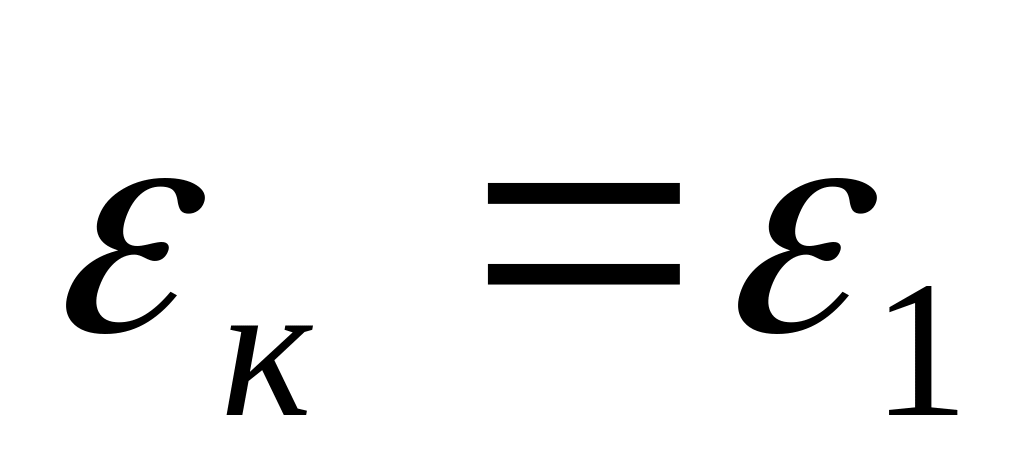• Приближаясь к первой молекуле, вторая под действием силы притяжения движется с все возрастающей скоростью. В результате:

- кинетическая энергия молекулы также растет.

- полная энергия системы, равная , остается неизменной (система двух молекул замкнута) и равной , так как одновременно уменьшается потенциальная энергия .

• При прохождении молекулой точки с координатой 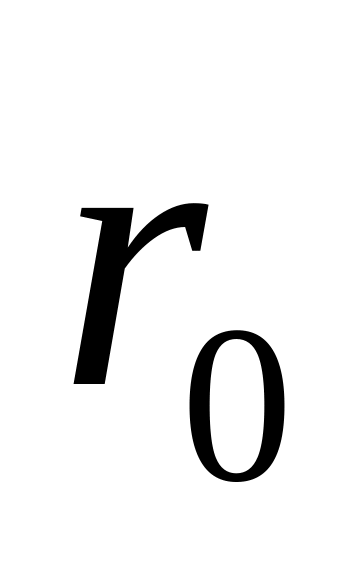силы притяжения сменяются силами отталкивания, вследствие чего молекула начинает быстро терять скорость (в области отталкивания кривая идет очень круто). В момент, когда потенциальная энергия становится равной полной энергии системы , скорость молекулы обращается в нуль. В этот момент имеет место наибольшее сближение молекул друг с другом.

• После остановки молекулы все явления протекают в обратной последовательности: сначала молекула движется с все возрастающей скоростью под действием силы отталкивания; миновав расстояние , молекула попадает под действие замедляющей ее движение силы притяжения и, наконец, удаляется на бесконечность, имея первоначальный запас кинетической энергии .

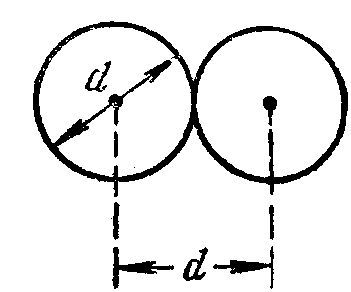
Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 2).

Величина называется эффективным сечением молекулы .

Из рис.1 видно, что в случае, когда молекула начинает свое движение из бесконечности с большим запасом энергии, минимальное расстояние, на которое сближаются центры молекул, оказывается меньшим (d₁ и d₂ на рисунке).

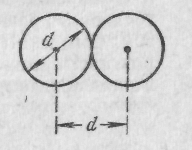
Таким образом, эффективный диаметр молекул зависит от их энергии, а следовательно, и от температуры. С повышением температуры эффективный диаметр молекул уменьшается.

За время между двумя последовательными соударениями молекула газа проходит некоторый путь , который называется длиной свободного пробега.

Длина свободного пробега — случайная величина. Иной раз молекуле удается пролететь между соударениями довольно большой путь, в другой раз этот путь может оказаться весьма малым.

Найдем вероятность различных значений .

Вероятность dP того, что молекула испытает соударение на отрезке пути ds, очевидно, пропорциональна величине этого отрезка и не зависит от того, какой путь уже прошла молекула без столкновений.

Взяв коэффициент пропорциональности в виде , получим, что

Вероятность — безразмерная величина, следовательно,

λ- имеет размерность длины.

Пусть из полного числа молекул путь s пролетели без столкновения N(s) молекул.

Из их числа претерпевает соударения на следующем за s отрезке ds количество молекул, равное .

Это количество представляет собой убыль величины N(s) на отрезке ds, т. е. – dN(s).

Таким образом,

Проинтегрировав, получаем .

Здесь = N(0) — число молекул, прошедших без столкновений путь, равный нулю, т. е. полное число молекул.

Отношение N(s) к дает вероятность P(s) того, что молекула пролетит, начиная с некоторого выбранного произвольно момента времени, путь s без столкновений:

Найдем среднее значение длины свободного пробега .

Для этого нужно знать вероятность dP_l того, что молекула, пролетев без столкновений путь , претерпит соударение на следующем за отрезке d .

Оба эти события, т. е. пролет без столкновений пути и соударение на отрезке d , статистически независимы. Следовательно, dP_l равна произведению вероятностей двух указанных событий.

Вероятность первого события равна .

Вероятность второго события в соответствии равна .

Таким образом,

Среднее значение :

Таким образом, обозначенная нами буквой λ величина совпадает со средней длиной свободного пробега.

За секунду молекула проходит в среднем путь, равный средней скорости .

Если за секунду она претерпевает в среднем столкновений, то средняя длина свободного пробега будет равна

Д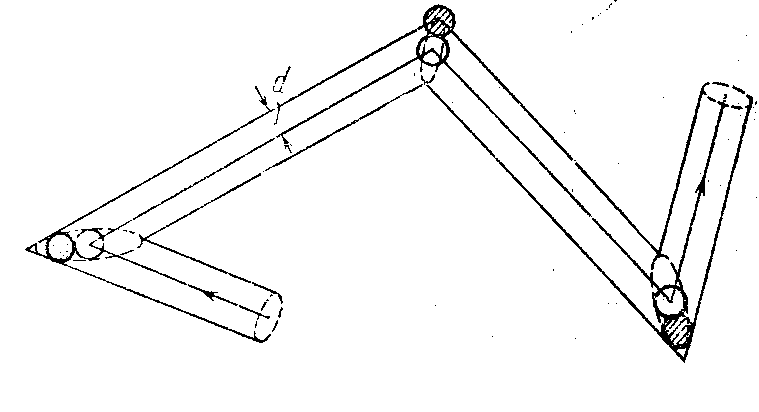 ля того чтобы подсчитать среднее число столкновений ,

• предположим вначале, что все молекулы, кроме данной, застыли неподвижно на своих местах.

• Проследим за движением выделенной нами молекулы.

- Ударившись об одну из неподвижных молекул, она будет лететь прямолинейно до тех пор, пока не столкнется с какой-либо другой неподвижной молекулой (рис.3).

- Это соударение произойдет в том случае, если центр неподвижной молекулы окажется от прямой, вдоль которой летит молекула, на расстоянии, меньшем эффективного диаметра молекулы d.

- В результате столкновения молекула изменит направление своего движения, после чего некоторое время опять будет двигаться прямолинейно, пока на ее пути снова не встретится молекула, центр которой будет находиться в пределах показанного на рис.3 цилиндра радиуса d.

• За секунду молекула проходит путь, равный .

• Число происходящих за это время соударений с неподвижными молекулами равно количеству молекул, центры которых попадают внутрь коленчатого цилиндра длины и радиуса d.

• Средняя длина свободного пробега много больше, чем эффективный диаметр молекул d.

• Поэтому объем цилиндра можно считать равным πd² .

• Умножив этот объем на число молекул в единице объема n, получим среднее число столкновений за секунду движущейся молекулы с неподвижными:

В действительности все молекулы движутся, и число соударений определяется средней скоростью движения молекул по отношению друг к другу, а не средней скоростью молекул относительно стенок сосуда.

Относительная скорость двух произвольно взятых молекул равна

Возведя это соотношение в квадрат, получим

Начало формы

Конец формы

(мы воспользовались тем, что ).

Среднее значение суммы нескольких величин равно сумме средних значений складываемых величин. Поэтому

События, заключающиеся в том, что первая молекула имеет скорость , а вторая — скорость , являются статистически независимыми.

Поэтому .

Для газа, находящегося в равновесии, каждый из сомножителей равен нулю. Таким образом,

(среднее значение квадрата скорости всех молекул одинаково и равно ).

Среднее число столкновений за секунду

и средняя длина свободного пробега:

Заменив πd² через σ (где эффективное сечение молекулы) , получаем

При постоянной температуре n пропорционально р (р=nkT).

Следовательно, средняя длина свободного пробега обратно пропорциональна давлению:

Эффективный диаметр молекул убывает с ростом температуры, поэтому при повышении температуры длина свободного пробега увеличивается.