
- •Содержание
- •Тема 1 6
- •Введение
- •Тема 1 Матрицы
- •Примеры решения задач
- •Тема 2 Свойства определителей
- •Примеры решения задач
- •Тема 3 Обратная матрица. Матричные уравнения.
- •Примеры решения задач
- •Тема 4 Система линейных алгебраических уравнений (слау)
- •Примеры решения задач
- •Тема 5 Ранг матрицы слау.
- •Примеры решения задач
- •Тема 6 Однородная система линейных уравнений. Фср.
- •Примеры решения задач
- •Тема 7 Линейная зависимость векторов. Базис и размерность линейного пространства.
- •Примеры решения задач
- •Тема 8 Линейные операторы.
- •Тема 9 Квадратичные формы.
- •Тема 10 Аналитическая геометрия на плоскости. Простейшие задачи.
- •Тема 11 Кривые второго порядка.
- •Тема 12 Прямая и плоскость в пространстве.
- •Тема 13 Векторная алгебра.
- •Справочные материалы
- •Перечень умений
- •Литература
Тема 2 Свойства определителей
Контрольные вопросы.
Что значить разложить определитель по элементам строки (столбца).
Запишите схематично «правило треугольника».
Запишите теорему Лапласа.
Сформулируйте свойства определителя и на примере определителя 3-го порядка, написанного в общем виде докажите их.
Примеры решения задач
Пример 1.
Вычислит величину определителя
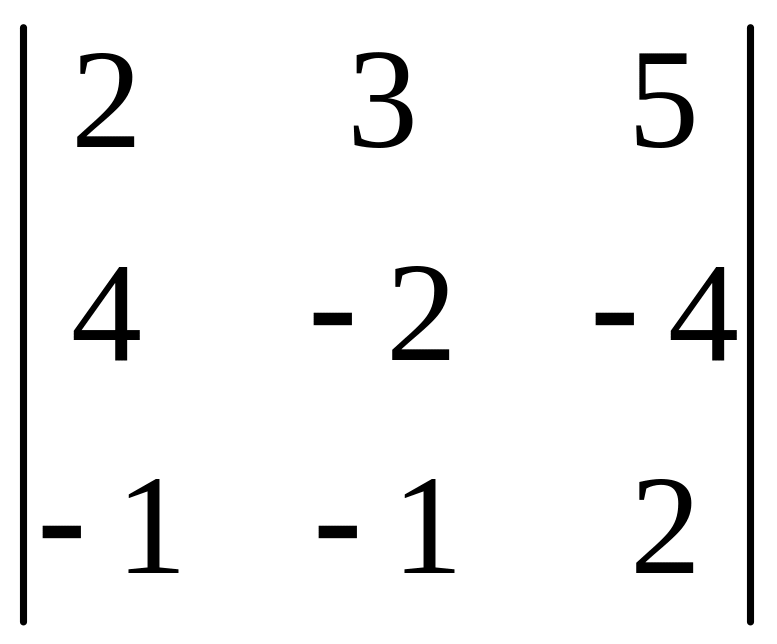 .
.
Решение. Рассмотрим три способа нахождения величины определителя.
1 способ основан на разложении определителя (теорема Лапласа), например, по первой строке.
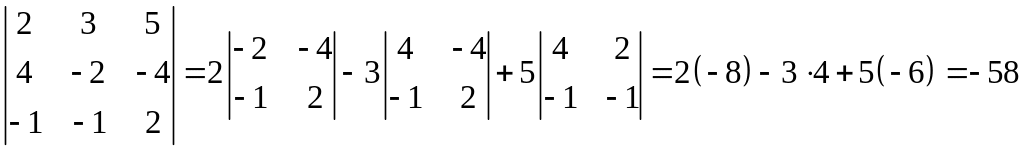 .
.
2 способ использует правило треугольников (правило Саррюса).
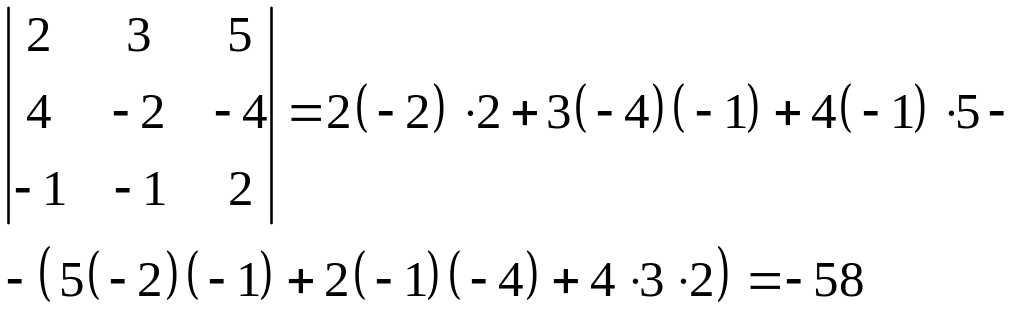
3 способ основан на приведении определителя к треугольному виду. Определитель же треугольной матрицы равен произведению её диагональных элементов.
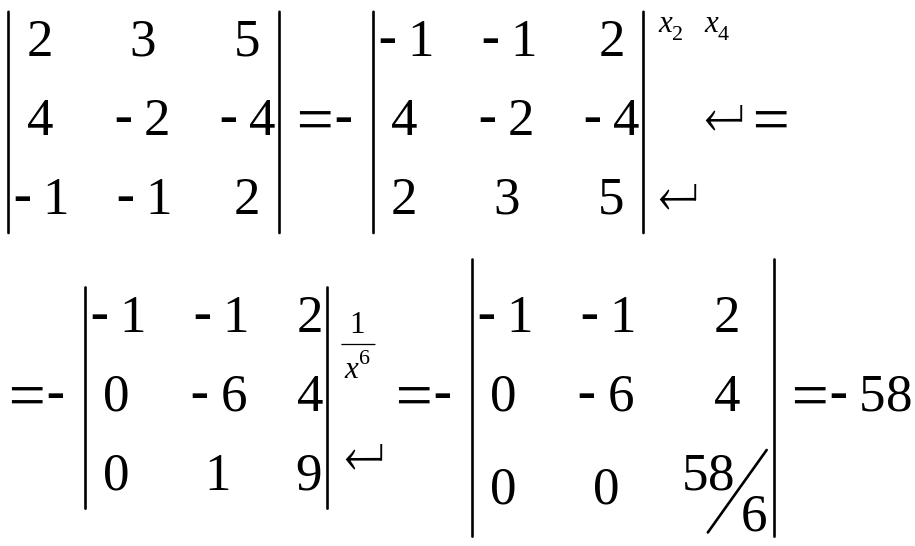
Последний способ прекрасно работает с большими определителями.
Задания.
Вычислите определители 2-го порядка
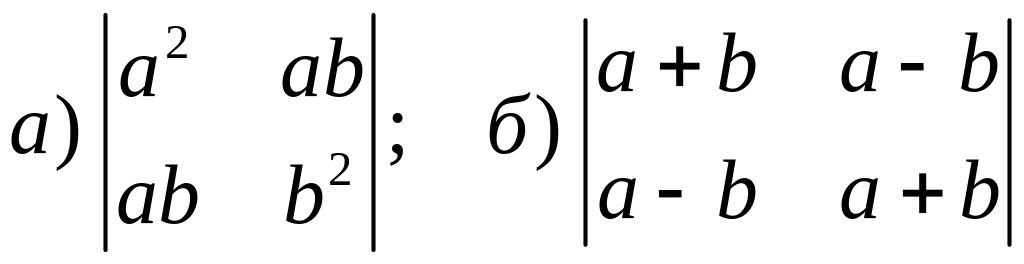
Вычислите определитель 3-го порядка
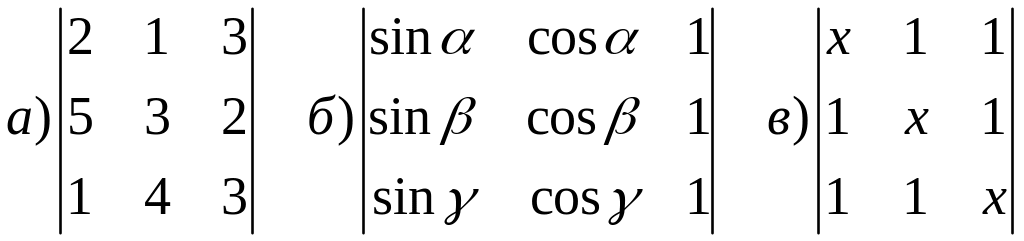
Решите уравнение
![]()
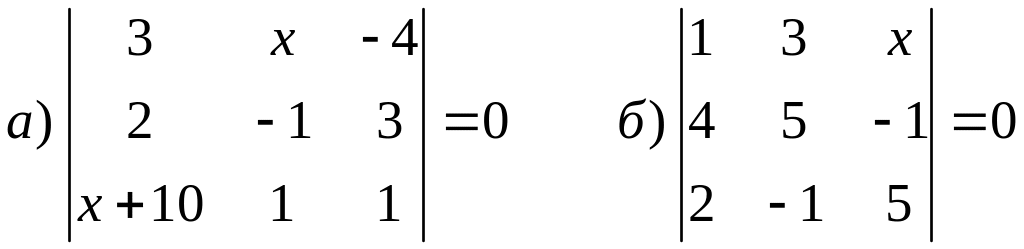
Решите неравенство
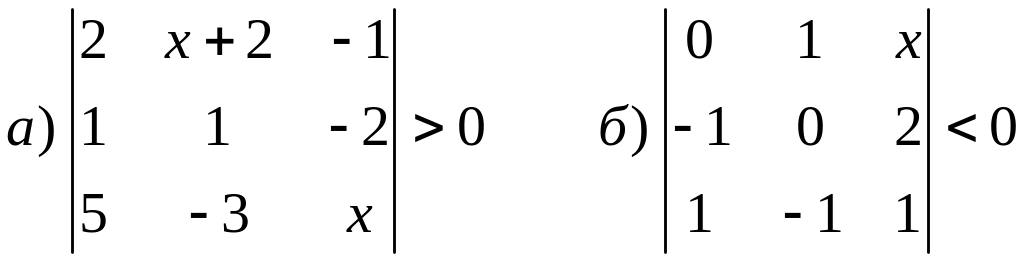
Используя свойства определителя доказать следующие тождества (определители не развертывать):
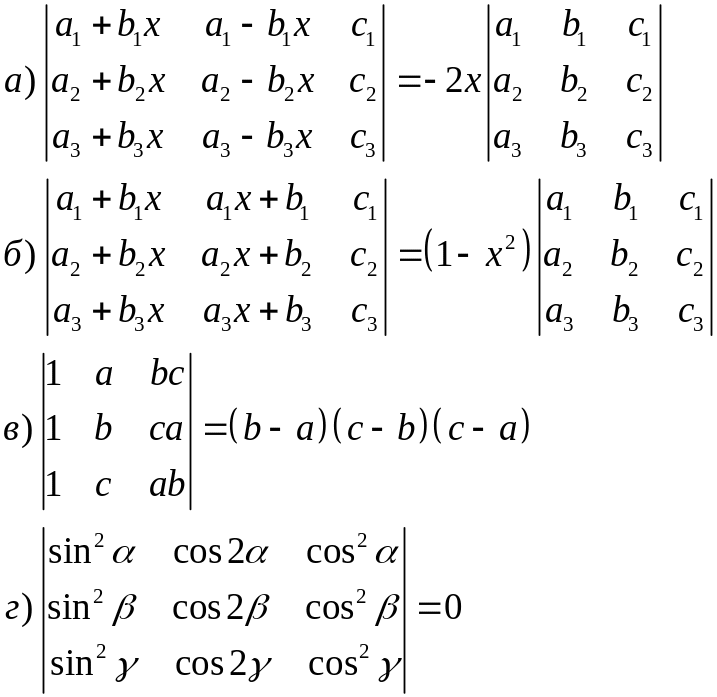
Вычислить следующие определители используя свойства
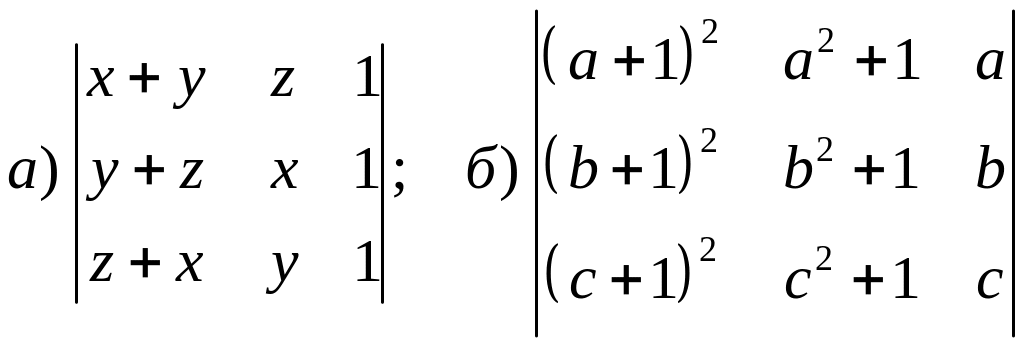
Вычислить определители; получив максимальное число нулей в строке или столбце:
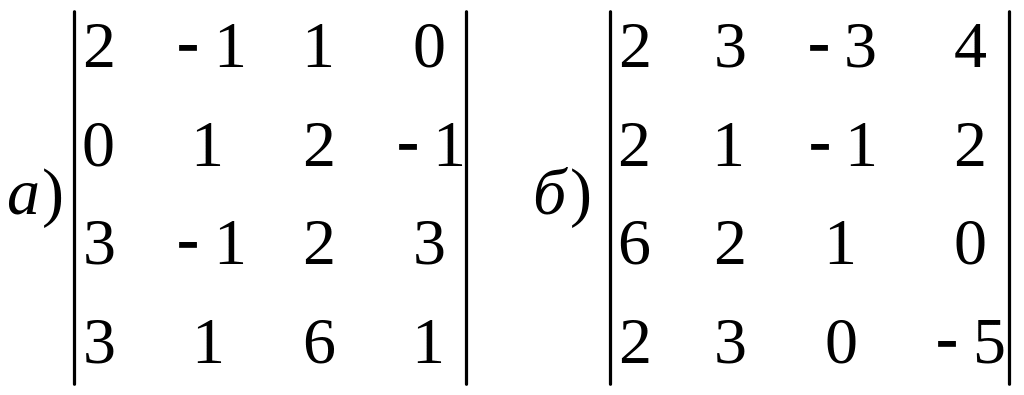
Вычислить определитель 6-го порядка, элементы которого заданы условиями
 .
.Вычислить определитель 6-го порядка, элементы которого заданы условиями
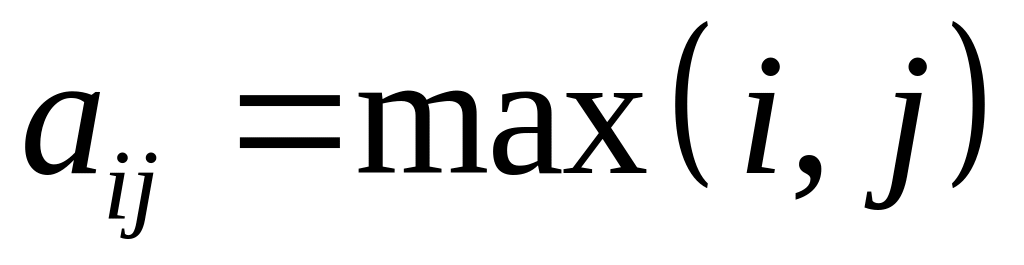
Найти значение параметра С, при котором величина определителя матрицы
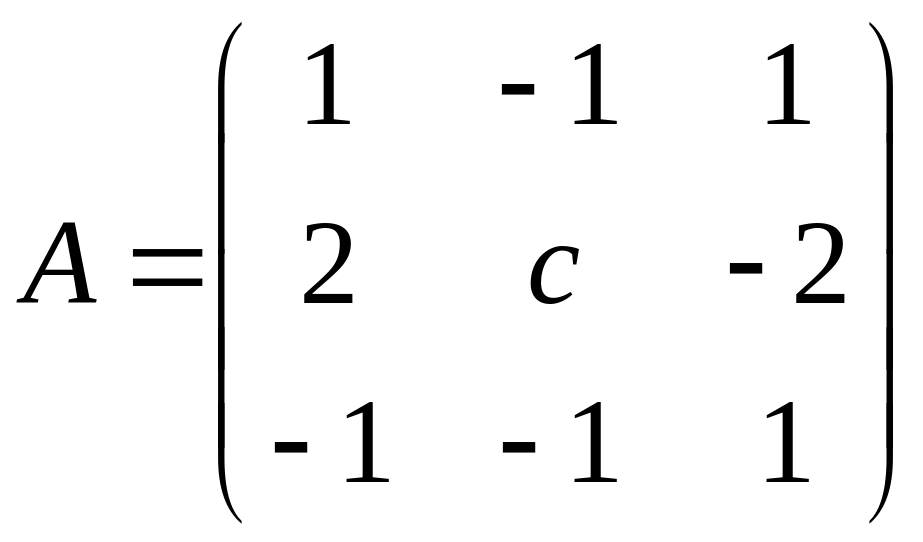 станет равной
станет равной
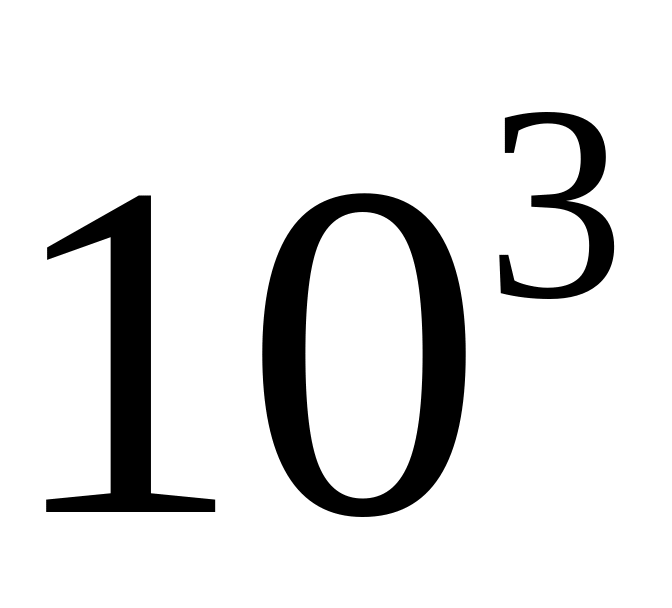 .
.
Тема 3 Обратная матрица. Матричные уравнения.
Контрольные вопросы.
Какая матрица называется обратной по отношению к матрице .
Свойства обратных матриц.
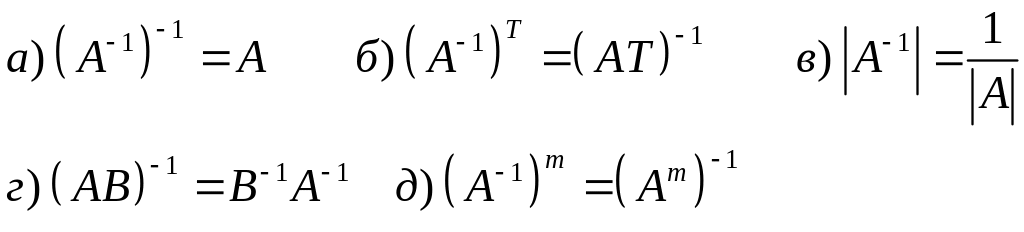
Какая матрица имеет обратную?
Формула для вычисления
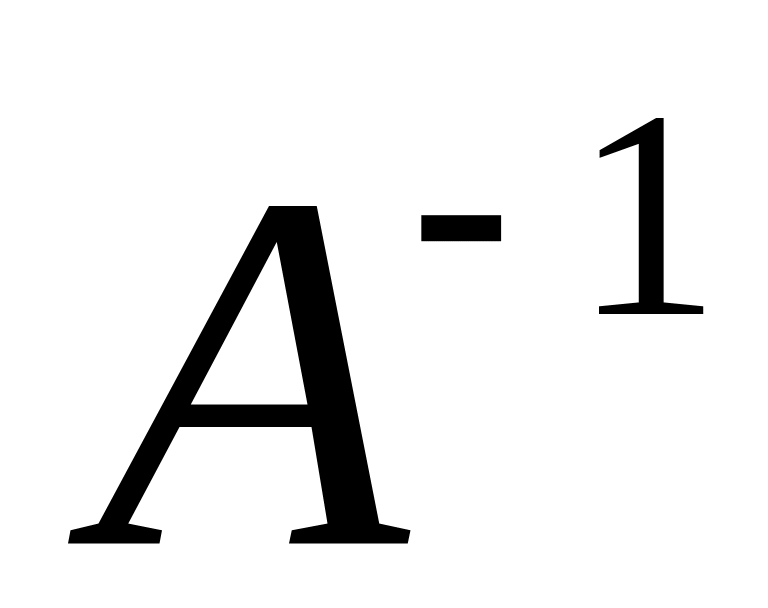 .
.Запишите решение для матричных уравнений вида:
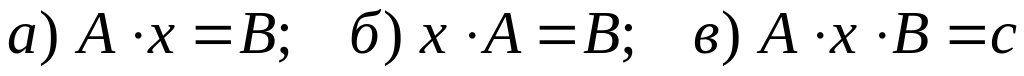 .
.
Примеры решения задач
Пример 1.
Для матрицы
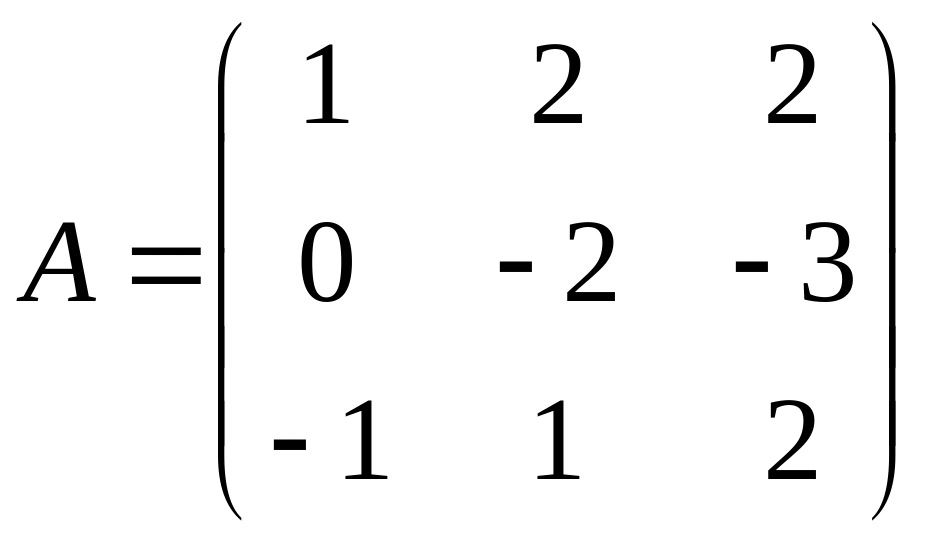 найти обратную
найти обратную
![]() .
.
Решение.
Метод присоединенной матрицы. Найдем
определитель матрицы
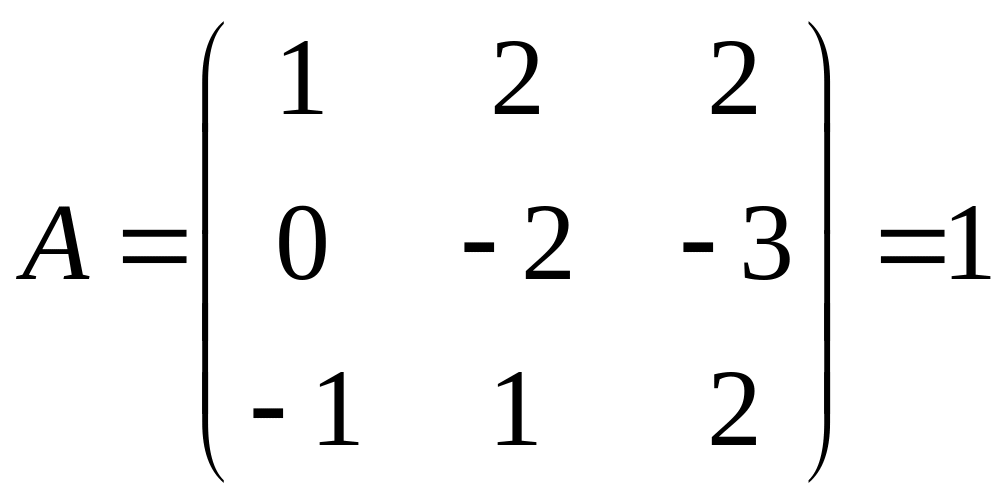 .
Транспонируем матрицу А.
.
Транспонируем матрицу А. 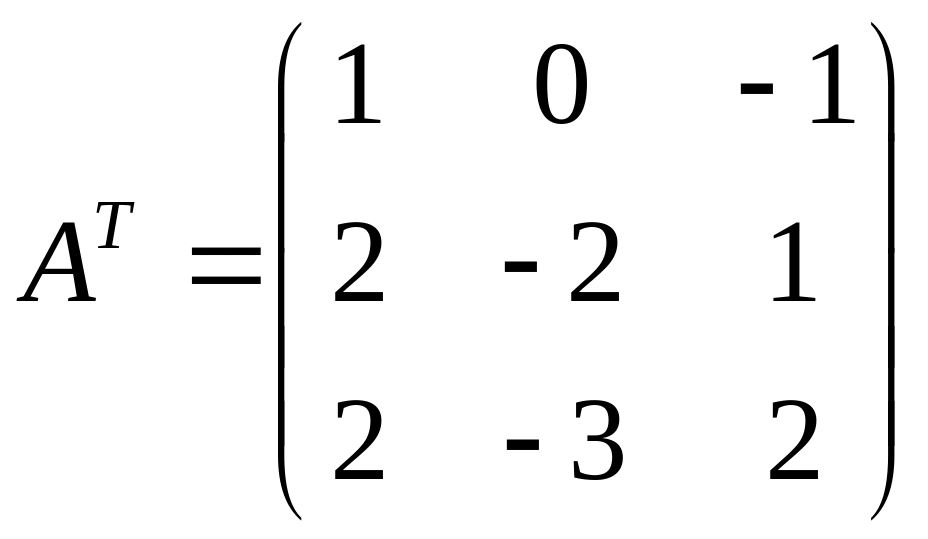 .
.
Составим
присоединенную матрицу из алгебраических
дополнений к элементам транспонированной.
Например,
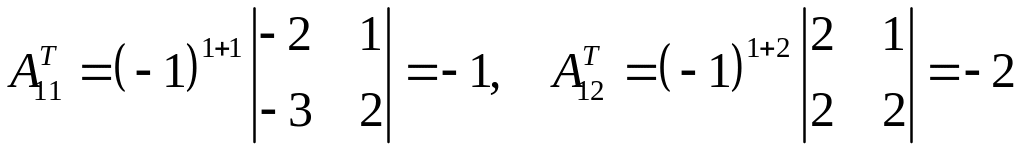 и так далее. Тогда
и так далее. Тогда
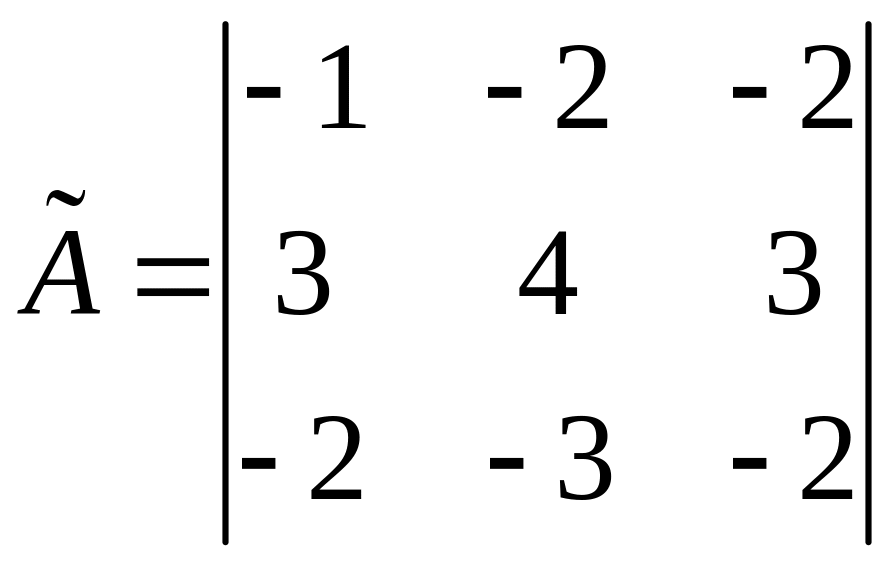 обратная матрице вычисляется по такой
формуле:
обратная матрице вычисляется по такой
формуле:
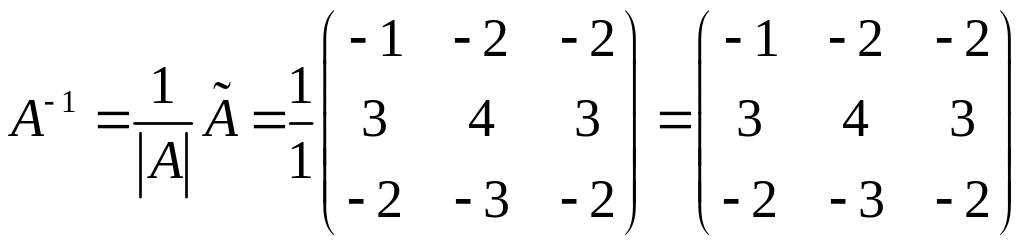 .
.
Пример 2.
Решить матричное уравнение, считая все
матрицы, участвующие в преобразованиях,
невырожденными.
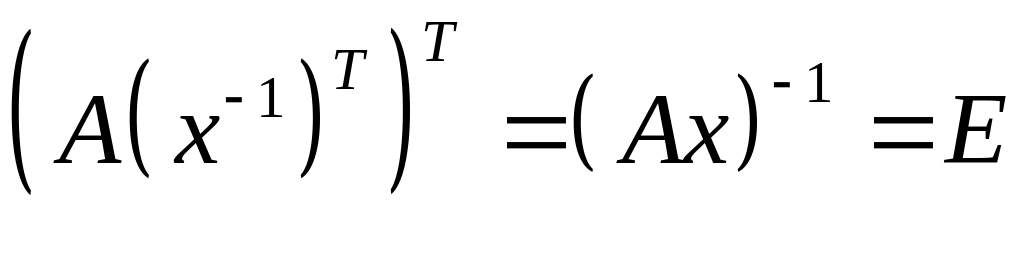 .
.
Решение.
Воспользуемся свойствами транспонированной
и обратной матриц:
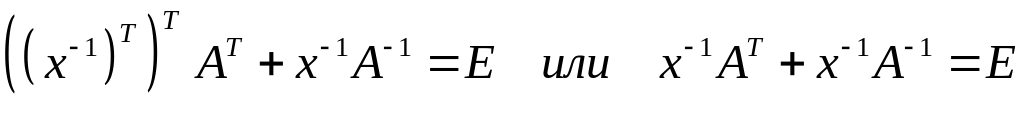 Вынесем
матрицу
Вынесем
матрицу
![]() за скобки и умножим уравнение слева на
матрицу
.
за скобки и умножим уравнение слева на
матрицу
.
![]() .
Таким образом, решением матричного
уравнения является матрица
.
Таким образом, решением матричного
уравнения является матрица
![]() .
.
Задания.
При каких значениях
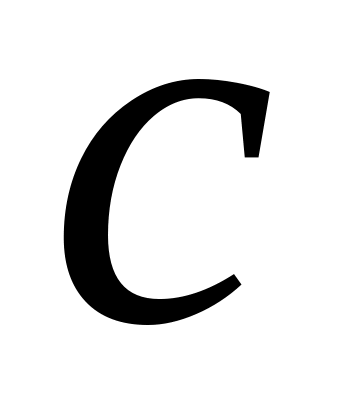 матрица
не имеет обратной
матрица
не имеет обратной
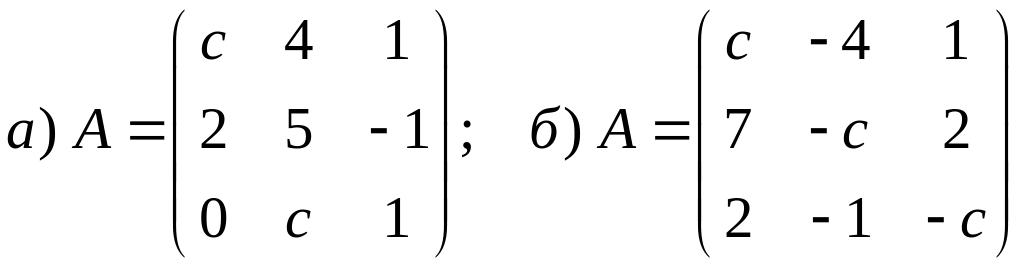
Найти
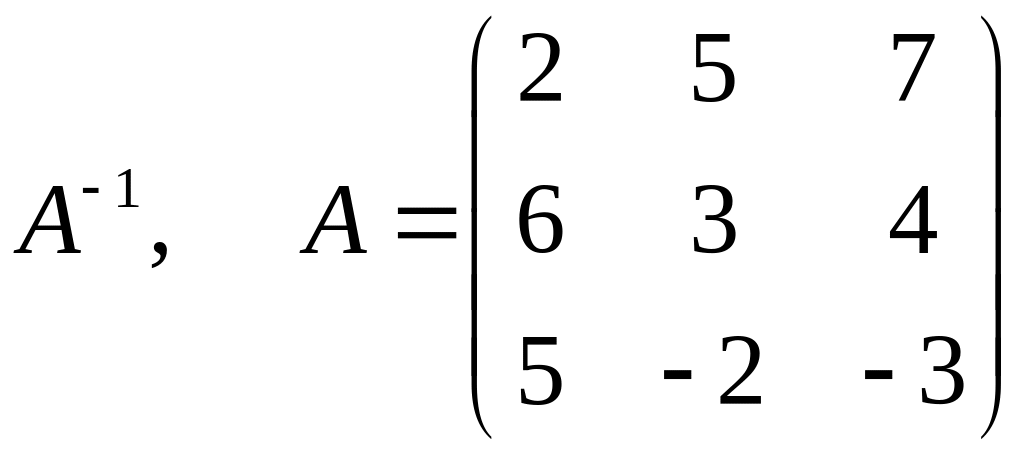
Решить матричные уравнения
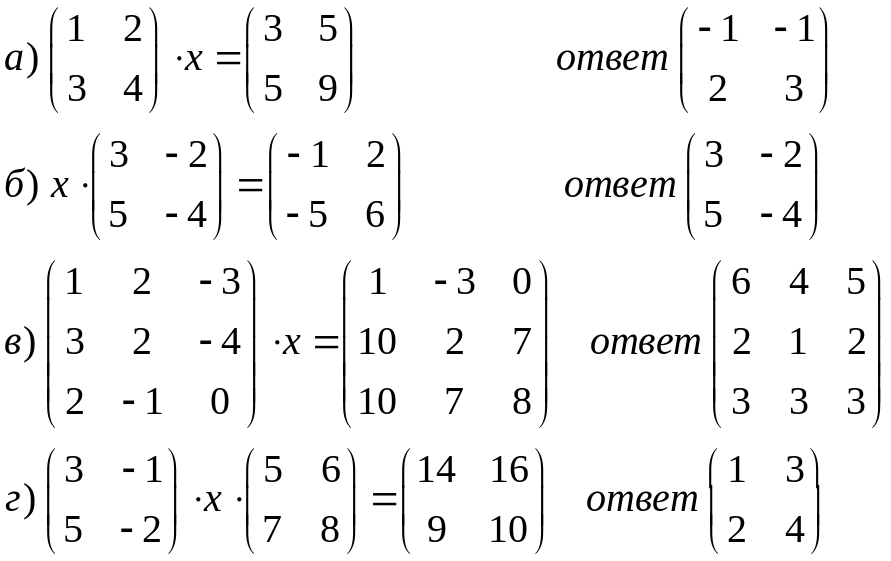
Вычислить значение
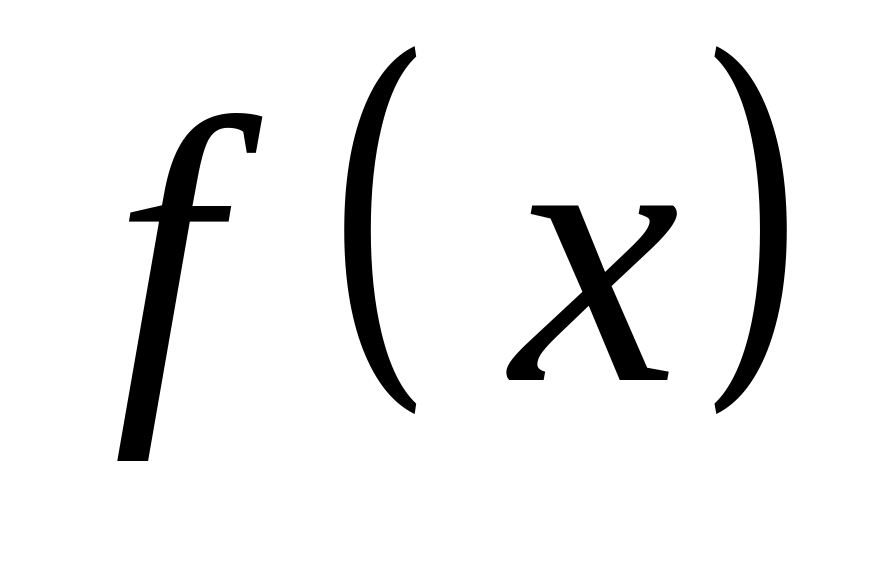 при
при
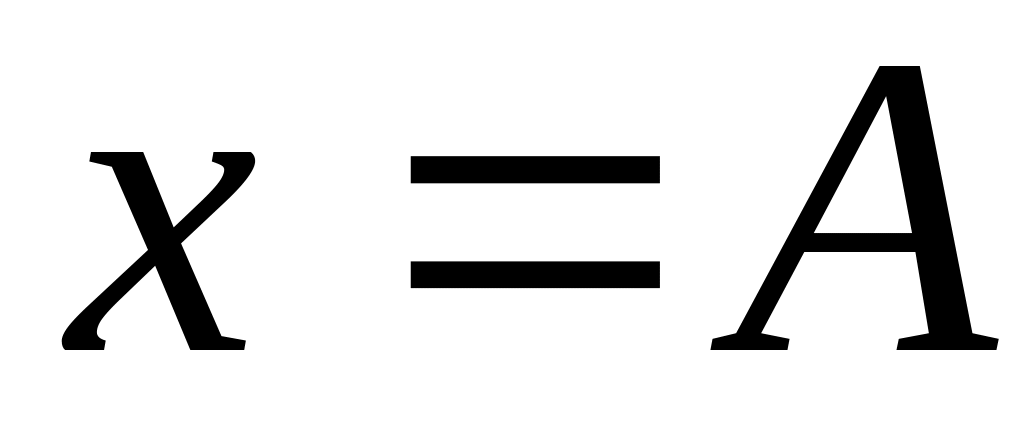
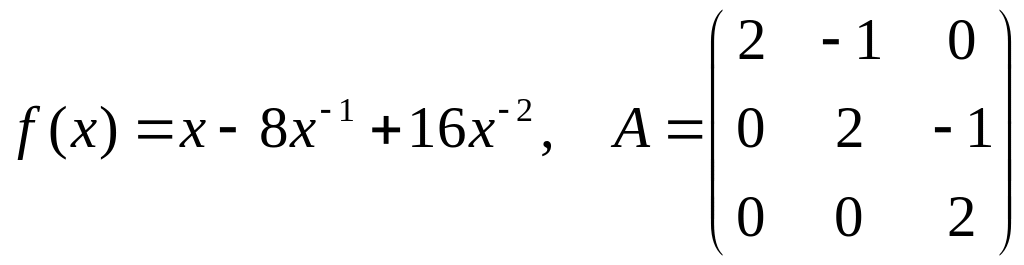
Решить систему матричных уравнений
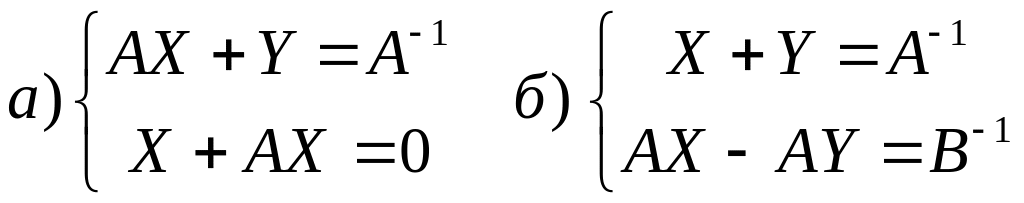
Решить матричные уравнения
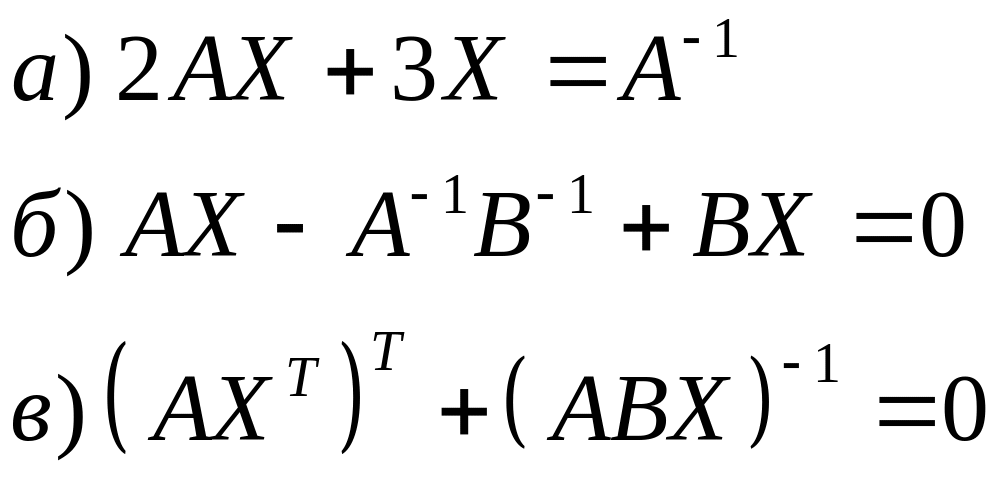
Тема 4 Система линейных алгебраических уравнений (слау)
Контрольные вопросы.
Когда система линейных уравнений называется Крамеровской?
Запишите формулы для нахождения решения такой системы.
Запишите в развернутом виде матричное уравнение:
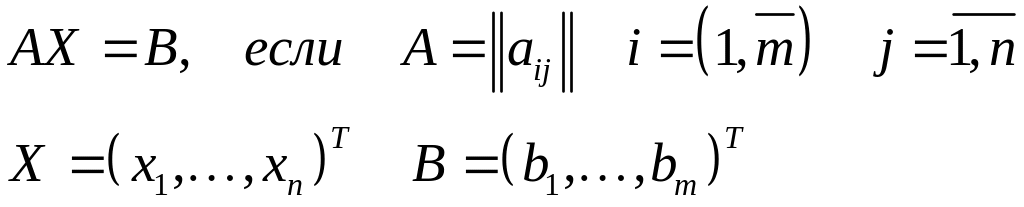
Что такое «прямой» ход метода Гаусса?
