Скорость упругой волны в однородном шнуре.

Рассмотрим поперечные колебания в однородном шнуре, плотность вещества которого - .

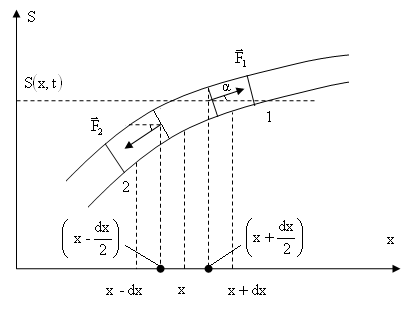
Выделим элемент с координатой и соседние с ним элементы: 1-й с координатой и 2-й с координатой .

Со стороны 1 и 2 элементов на выбранный элемент действуют силы натяжения и , причем

.

Запишем 2-й закон Ньютона

,

где - масса среднего элемента,

- его ускорение.

Спроецируем на ось

,

,

,

.

С учетом малости угла длина элемента шнура равна и

,

где - площадь поперечного сечения шнура.

Запишем

,

.

Мы получим волновые уравнения, из которого следует, что:

1. в шнуре распространяется волна

2. скорость волны равна

.

Колебания струны.

Закрепленный с обоих концов и натянутый шнур называется струной. При возникновении колебаний в струне устанавливаются стоячие волны.

В местах закрепления струны должны располагаться узлы стоячей волны.

Обозначим

- длина струны,

- длина бегущей волны,

- длина стоячей волны, .

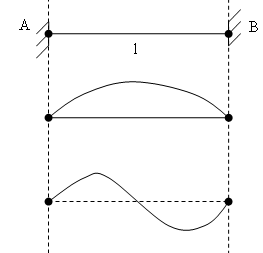
Очевидно, для того, чтобы в точках и находились узлы необходимо условие

,

Запишем для бегущей волны

,

,

,

Величина называется собственной частотой колебаний струны. Колебания струны с частотами называют собственными, нормальными или гармониками.

Величина называется основной частотой.

Звук.

Звуком или звуковыми волнами называются упругие волны, распространяющиеся в воздухе и имеющие частоту в интервале

.

Инфразвуком называют звуковые волны с частотой

.

Ультразвуком называют звуковые волны с частотой

.

Звуковые волны, достигая человеческого уха вызывают специфические ощущения, которые и называются звуком. С точки зрения воздействия на организм важное значение имеет интенсивность звуковых волн.

.

Для плоской гармонической звуковой волны

,

где - круговая частота колебаний частиц воздуха, ,

- амплитуда волны,

- плотность невозмущенного газа,

- скорость звуковой волны.

Минимальная интенсивность звуковой волны, которую человек еще ощущает как звук называется порогом слышимости

.

При значениях интенсивности звуковой волны, превышающих некоторое значение человек получает болевые ощущения. Значения называется порогом болевого ощущения

.

Уровнем громкости называется величина

, ,

, ,

Можно получить формулу, связывающую интенсивность звука с амплитудой избыточного давления

,

где - амплитуда избыточного давления.

Эффект Доплера для звуковых волн.

Пусть имеются источник и приемник звуковых волн. Пусть покоящийся источник излучает волну с частотой , которую принимает покоящийся приемник. Частота звука, регистрируемого приемником, будет также .

Пусть расстояние между и равно , скорость звука .

Найдем, сколько длин волн «укладывается» на расстоянии

, , ,

, , ,

где - время, за которое волна от источника дойдет до приемника.

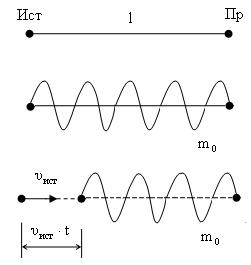
Пусть движется на встречу приемнику. За время источник пройдет расстояние и длин волн укладываются на меньшем расстоянии . Найдем длину волны

.

Запишем

,

где - частота звука, который регистрирует приемник

, .

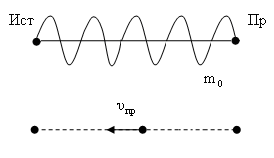
Пусть теперь приемник движется навстречу источнику со скоростью . За некоторое время приемник зарегистрирует колебаний

,

где - частота регистрируемых колебаний. Это число равно

.

Здесь - число колебаний, которое зарегистрировал бы за время неподвижный приемник, - число колебаний, которые приемник зарегистрирует дополнительно, вследствие своего движения навстречу источнику

, ,

, ,

Объединим , получим

.

, считается положительной, если движение происходит навстречу и отрицательной, если при движении источник и приемник удаляются друг от друга.