Интенсивность волны.

В случае гармонической волны есть периодическая функция времени

.

Следовательно,

.

Средние за период значение вектора плотности потока энергия, есть вектор равный:

,

,

.

Для гармонической волны

,

.

Интенсивность волны называется скалярная величина, равная модулю среднего за период значения, вектора плотности потока энергии волны

, .

Для гармонической волны:

,

,

.

Найдем среднее за период значение потока энергии гармонической волны

,

.

Пусть - плоский участок, перпендикулярный скорости волны.

,

.

Пусть имеет одно и тоже значение во всех точках поверхности .

,

.

Запишем отсюда

, .

Интенсивность волны есть величина равная энергии, переносимой в среднем за период в единицу времени через единичную площадку, перпендикулярную скорости волны.

Стоячие волны.

Опыт дает, что если в среде одновременно распространяется несколько упругих волн, то смещение частиц среды равно геометрической сумме смещений, которые частицы среды совершали бы при распространении каждой волны в отдельности.

Этот закон называется принципом суперпозиции для волн в среде. Пусть в точке оси находится источник волны, совершающий колебания по закону

.

В точке , находящейся на расстоянии от источника возбуждаются колебания

.

Далее, распространяясь вдоль , волна достигает границы среды, расположенной перпендикулярно на расстоянии от источника. Для границы можем записать в общем случае

,

где - плотность вещества среды.

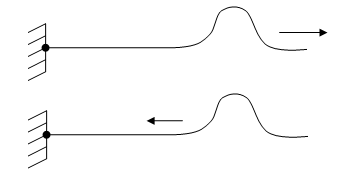
После того, как волна достигает точку , возникает волна, распространяющаяся в обратном направлении, которая приходит в точку

Здесь учитывает возможное изменение фазы волны в результате отражения. В точку приходят колебания как от волны , распространяющейся к границе раздела сред, так и волна , возникающая при отражении и распространяющейся в обратном направлении.

Выберем момент отсчета времени так, чтобы .

Первый множитель, содержащий косинус, не зависит от времени .

Обозначим

.

Тогда

,

.

Выражение определяет стоячую волну, - амплитуда стоячей волны.

Волны и называются бегущими.

Узлы и пучности стоячей волны.

Выражение для стоячей волны описывает гармонические колебания частиц среды в разных точках.

Запишем

.

Точки, в которых амплитуда стоячей волны максимальна, называется пучностями.

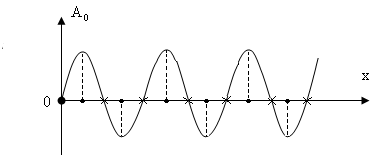
Найдем координаты пучностей

,

,

,

,

.

Точки, в которых амплитуда стоячей волны равна нулю, называется узлами.

,

,

,

.

Расстояние между соседними пучностями или соседними узлами называется длиной стоячей волны

,

.

Значения определяется следующими условиями

, ,

, .

Поток энергии в стоячей волне.

Найдем среднее за период значение потока энергии для стоячей волны в произвольной точке .

.

Очевидно, что для падающей и отраженной волн:

,

.

Отсюда

.

Средний по времени поток энергии в любом сечении стоячей волны равен нулю.