
- •П.2 Математический маятник.
- •П.3 Физический маятник.
- •Свободные колебания.
- •Период и частота колебаний.
- •Кинематика и динамика свободных гармонических колебаний.
- •Вектор – амплитуда.
- •Сложение гармонических колебаний.
- •П.1 Одинаково направленные колебания различной частоты.
- •Взаимно перпендикулярные колебания.
- •Ангармонические (негармонические) колебания.
- •Свободные затухающие колебания.
- •Энергия затухающих колебаний.
- •Характеристики затухающих колебаний.
- •Апериодическое движение.
- •Дифференциальное уравнение для колебательного контура.
- •Свободные колебания в контуре без сопротивления.
- •Свободные затухающие колебания в контуре с сопротивлением.
- •Заряд, напряжение, ток, энергия в колебательном контуре с сопротивлением.
- •Переменный ток.
- •Мощность в цепи переменного тока.
- •Возникновение и распространение упругой волны.
- •Уравнение волны.
- •П.1 уравнение плоской гармонической волны.
- •П.2 Уравнение сферической гармонической волны.
- •П.3 Уравнение плоской гармонической волны, распространяющейся в произвольном направлении.
- •Волновое уравнение.
- •Скорость упругой волны в твердой среде.
- •Скорость упругой волны в газе.
- •Скорость упругой волны в однородном контуре.
- •Энергия упругой волны.
- •Плотность потока энергии.
- •Интенсивность волны.
- •Стоячие волны.
- •Узлы и пучности стоячей волны.
- •Поток энергии в стоячей волне.
- •Скорость упругой волны в однородном шнуре.
- •Колебания струны.
- •Эффект Доплера для звуковых волн.
- •Электрические волны.
- •Плоская электромагнитная волна.
- •Энергия электромагнитной волны.
- •Плотность потока энергии электромагнитной волны.
- •Интенсивность волны.
- •Импульс электромагнитной волны.
- •Давление электромагнитной волны.
- •Излучение электромагнитных волн.
- •Эффект Доплера для электромагнитных волн.
Скорость упругой волны в однородном контуре.
Рассмотрим
поперечные колебания в однородном
контуре, плотность вещества которого
-
![]() .
.
Выделим элемент
с координатой
и соседние с ними элементы: 1-й с координатой
и 2-й с координатой
![]() .
.
Со стороны 1 и 2
элементов на выбранный элемент действуют
силы натяжения
![]() и
и
![]() ,
причем
,
причем
![]() .
.
Запишем 2-й закон Ньютона
![]() ,
,
где
![]() -
масса среднего элемента,
-
масса среднего элемента,
![]() - его ускорение.
- его ускорение.
Спроецируем на ось
![]() ,
,
![]() ,
,
![]() ,
,
 .
.
С учетом скорости угла длина элемента шнура равна и
![]() ,
,
где - площадь поперечного сечения шнура.
Запишем
![]() ,
,
![]() .
.
Мы получили волновое уравнение, из которого следует, что:
в шнуре распространяется волна
![]() ,
,
скорость волны равна
![]() .
.
Энергия упругой волны.
В среде, в которой
распространяется продольная упругая
волна, выделим элемент массой
![]()
![]() ,
,
где - плотность вещества среды,
![]() -
объем элемента.
-
объем элемента.
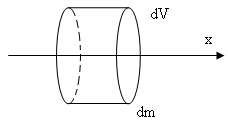
Обозначим
- смещение элемента вследствие его колебаний,
![]() -
скорость элемента.
-
скорость элемента.
Кинетическая энергия данного элемента равна
![]() ,
,
![]() .
.
Вследствие деформации элемент обладает такой потенциальной энергией упругой деформации
![]() ,
,
где
![]() - жесткость,
- жесткость,
![]() - деформация
элемента.
- деформация
элемента.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Для твердой упругой среды
,
![]() ,
,
где - фазовая скорость упругой волны
![]() .
.
Полная механическая энергия элемента равна
![]() ,
,
![]() .
.
Объемная плотность энергии равна
![]() ,
,
![]() ,
,
![]() .
.
Для плоской гармонической волны:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Энергия волны в объеме среды равна
![]() .
.
Средним значением объемной плотности энергии упругой волны за период колебаний называется величина
![]() .
.
Для плоской гармонической волны
 ,
,
![]() .
.
Плотность потока энергии.
Поток энергии через некоторую поверхность есть скалярная величина, равная отношению энергии, переносимый через поверхность за некоторый элементарный промежуток времени и длительности этого промежутка.
![]() ,
,
![]() .
.
В случае, если поверхность - элементарная, говорят об элементарном потоке энергии
![]() .
.
При распространении упругой волны частиц среды приобретают дополнительную энергию. Следовательно, при этом происходит перенос энергии волной.
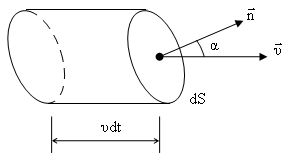
В среде распространяется упругая волна со скоростью . Выделим элемент среды в виде элементарного объема
![]() ,
,
- угол между вектором нормали к элементу и вектором скорости волны.
Колебания от всех
частиц среды внутри объема достигнут
элемента
за время
![]() .
Вместе с ними через
переносится энергия, равная энергии
колебаний в данном элементарном объеме.
.
Вместе с ними через
переносится энергия, равная энергии
колебаний в данном элементарном объеме.
![]() .
.
Поток энергии через элементарный участок равен
![]() ,
,
![]() .
.
Поток энергии через поверхность , проведенную в среде, равен
![]() ,
,
![]() .
.
Найдем элементарный
поток энергии через элементарный участок
![]() ,
перпендикулярный скорости волны
.
,
перпендикулярный скорости волны
.

![]() .
.
Запишем
![]() ,
,
![]()
![]() ,
,
![]() .
.
Вектор
![]() называется плотностью потока энергии
илли вектором Умова.
называется плотностью потока энергии
илли вектором Умова.
Плотнось потока энергии есть вектор, направление которого совпадает с вектором скорости упругой волны, а модуль равен энергии,переносимый упругой волной в единицу времени через единичную площадку, перпендикулярную скорости волны.
Теперь можем записать:
![]() ,
,
![]() .
.
