Переменный ток.

Пусть в контуре действует переменная э.д.с

.

Сила тока в контуре

,

,

Для можно получить

.

Обозначим

, Ом

Величина называется полным электрическим сопротивлением или

Электрическое сопротивление называется активным сопротивлением

, Ом

, Ом

Величина называется реактивным индуктивным сопротивлением.

Величина называется реактивным емкостным сопротивлением

,

, Ом

Величина есть реактивное сопротивление.

Можно записать для амплитуды силы тока.

,

Для величины запишем

= .

Величина имеет смысл закона Ома для амплитудных значений напряжения и тока.

Мощность в цепи переменного тока.

Найдем мощность переменного тока

,

,

.

Среднее за период значение мощности:

,

,

,

,

,

,

,

, .

Такую же мощность может развивать постоянный ток для некоторого

, ,

,

.

Величина , называются амплитудными значениями , а - действующими (эффективными) значениями силы тока и напряжения.

Глава: Волны в среде.

Тело, непрерывно распределенное в пространстве, называется средой. Элемент среды называется частицей среды.

Возникновение и распространение упругой волны.

Пространственная модель среды – это одномерная цепочка атомов с упругими связями между ними.

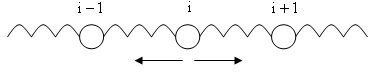
Пусть -ый атом под действием внешней силы совершает колебания, например, вдоль цепочки. Вследствие деформации «пружинок» на соседние и атомы начинает действовать переменная сила, вызывающая их вынужденные колебания с той же частотой. В свою очередь эти атомы вовлекают в колебательный процесс соседние с ними и т.д. в них происходит распространение колебательного процесса вдоль цепочки атомов.

Процесс распространения колебаний в среде называется упругой волной.

Частица среды, колебания которой приводят к возникновению волны, называется источником волны.

Упругая волна называется продольной, если колебания частиц среды происходят в направлении перпендикулярном направлению распространения волны.

Совокупность точек среды, до которых в данный момент дошли колебания, называется волновым фронтом или фронтом волны.

Среди множества частиц, совершающих колебания, можно выделить частицы имеющие одинаковую фазу колебаний.

Совокупность точек среды, совершающих колебания с одинаковой фазой, называются волновой поверхностью.

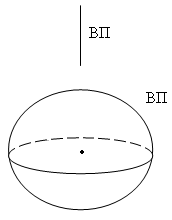
Если волновая поверхность представляет собой плоскость, то волна называется плоской.

Если волновая поверхность – сфера, то волна называется сферической.

Уравнение волны.

Обозначим:

- смещение частицы среды из положения равновесия, м.

в общем случае смещение является функцией координат точек среды и времени:

.

Это выражение имеет смысл уравнения волны.

П.1 уравнение плоской гармонической волны.

Пусть колебания частиц среды носят гармонический характер и распространяются вдоль оси .

Все точки волновой поверхности совершают колебания одинаковым образом. В то же время эти точки имеют одинаковые координаты и различные и .

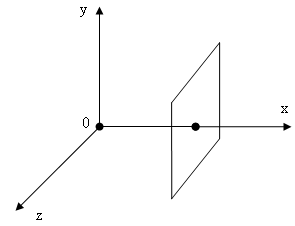
Для того чтобы уравнение было справедливым для всех точек волновой поверхности необходимо, чтобы в нем не было зависимости от и ., т.е.

.

Пусть колебания точек в плоскости имеют вид:

,

.

Найдем колебания точек в плоскости с произвольной координатой .

Обозначим

- скорость распространения колебаний или скорость волны.

Для того, чтобы колебания от дошли до плоскости требуется время

.

Колебания точек, лежащих в плоскости будут отставать по времени на от колебаний частиц в плоскости и будут иметь вид:

,

,

.

Здесь:

- амплитуда волны,

- круговая (циклическая) частота волны,

- частота волны,

- период колебаний, - фаза волны,

- начальная фаза источника волны,

Уравнение есть уравнение плоской гармонической волны.

Зафиксируем значение фазы

,

.

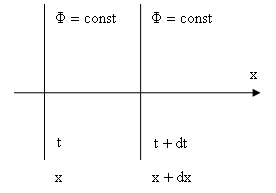
Для выполнения этого условия необходимо, чтобы с увеличением времени происходило увеличение значения , а это означает, что поверхность перемещается вдоль оси .

Продифференцируем по

,

,

.

Скорость распространения волны есть скорость перемещения поверхности постоянной фазы. Скорость волны называется фазовой скоростью.

Т.к. , то . Следовательно, уравнение описывает волну, распространяющуюся в положительном направлении оси

,

,

.

Перепишем уравнение

.

Длиной волны называется расстояние, которое волна проходит за время, равное периоду колебаний

,

.

Волновым числом называется величина

, ,

,

.

Очевидное соотношение

.

Запишем уравнения, определяющие колебания в двух точках с координатами и

,

.

Разностью фаз колебаний точек среды называется величина

.

Вычислим величину

.

Обозначим

,

,

.

Рассмотрим два случая.

Пусть ,

.

Длина волны равна расстоянию между двумя ближайшими точками, лежащими на прямой вдоль которой распространяется волна, разность фаз колебаний которых равна .

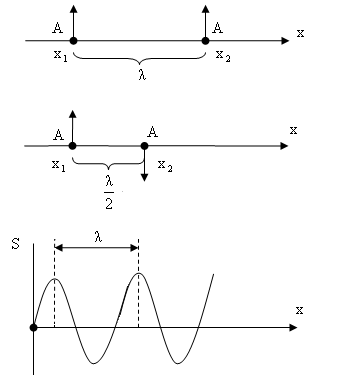
Пусть теперь ,

.

Частицы совершают колебания с противоположными фазами. В случае если при распространении колебаний энергия волны поглощается средой, то амплитуда колебаний уменьшается и происходит затухание волны.

,

где - коэффициент затухания волны,

- амплитуда в точках плоскости .