
- •П.2 Математический маятник.
- •П.3 Физический маятник.
- •Свободные колебания.
- •Период и частота колебаний.
- •Кинематика и динамика свободных гармонических колебаний.
- •Вектор – амплитуда.
- •Сложение гармонических колебаний.
- •П.1 Одинаково направленные колебания различной частоты.
- •Взаимно перпендикулярные колебания.
- •Ангармонические (негармонические) колебания.
- •Свободные затухающие колебания.
- •Энергия затухающих колебаний.
- •Характеристики затухающих колебаний.
- •Апериодическое движение.
- •Дифференциальное уравнение для колебательного контура.
- •Свободные колебания в контуре без сопротивления.
- •Свободные затухающие колебания в контуре с сопротивлением.
- •Заряд, напряжение, ток, энергия в колебательном контуре с сопротивлением.
- •Переменный ток.
- •Мощность в цепи переменного тока.
- •Возникновение и распространение упругой волны.
- •Уравнение волны.
- •П.1 уравнение плоской гармонической волны.
- •П.2 Уравнение сферической гармонической волны.
- •П.3 Уравнение плоской гармонической волны, распространяющейся в произвольном направлении.
- •Волновое уравнение.
- •Скорость упругой волны в твердой среде.
- •Скорость упругой волны в газе.
- •Скорость упругой волны в однородном контуре.
- •Энергия упругой волны.
- •Плотность потока энергии.
- •Интенсивность волны.
- •Стоячие волны.
- •Узлы и пучности стоячей волны.
- •Поток энергии в стоячей волне.
- •Скорость упругой волны в однородном шнуре.
- •Колебания струны.
- •Эффект Доплера для звуковых волн.
- •Электрические волны.
- •Плоская электромагнитная волна.
- •Энергия электромагнитной волны.
- •Плотность потока энергии электромагнитной волны.
- •Интенсивность волны.
- •Импульс электромагнитной волны.
- •Давление электромагнитной волны.
- •Излучение электромагнитных волн.
- •Эффект Доплера для электромагнитных волн.
Дифференциальное уравнение для колебательного контура.
Рассмотрим
колебательный контур, содержащий
конденсатор
,
катушку индуктивности
![]() ,
сопротивление проводников обозначим
,
сопротивление проводников обозначим
![]() .
Пусть в момент
от обкладки
.
Пусть в момент
от обкладки
![]() конденсатора начинает течь ток. Пусть
в этот же момент в контуре начинает
действовать э.д.с., которую обозначим
.
конденсатора начинает течь ток. Пусть
в этот же момент в контуре начинает
действовать э.д.с., которую обозначим
.

Запишем закон Ома:
![]() ,
,
![]() ,
,
где
![]() - заряд, появившийся на обкладках
конденсатора в результате протекания
в цепи тока.
- заряд, появившийся на обкладках
конденсатора в результате протекания
в цепи тока.
Далее:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если найти решение
уравнения
![]() ,
то можно определить закон силы тока
,
то можно определить закон силы тока
![]() .
.
Свободные колебания в контуре без сопротивления.
Электромагнитные колебания называются свободными, если в контуре не действует переменная э.д.с.
Итак,
![]() и
и
![]() .
.
![]() .
.
Обозначим:
![]() ,
,
![]() .
.
Решение уравнения имеет вид
![]() ,
,
![]() .
.
Величина
есть круговая частота собственных
свободных колебаний или собственная
частота контура.
![]() -
амплитуда заряда на конденсаторе.
-
амплитуда заряда на конденсаторе.
Период колебаний равен
![]() ,
,
![]() .
.
Это формула Томсона.
Напряжение на конденсаторе равно
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
амплитуда напряжения на конденсаторе.
-
амплитуда напряжения на конденсаторе.
Сила тока в контуре
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
амплитуда тока в контуре.
-
амплитуда тока в контуре.
Энергия электрического поля
![]() .
.
Энергия магнитного поля
![]() ,
,
![]() .
.
Энергия электрического и магнитного полей или энергия контура
![]() ,
,
![]() ,
,
![]() .
.
Свободные затухающие колебания в контуре с сопротивлением.
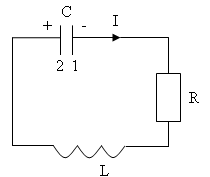
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() - коэффициент
затухания колебаний.
- коэффициент
затухания колебаний.
Решение уравнений имеет вид
![]() ,
,
,
- круговая (циклическая) частота затухающих колебаний.
![]() .
.
Периодом затухающих колебаний называется величина
,
.
Логарифмический декремент затухающих колебаний равен
![]() ,
,
![]() .
.
В случае малого затухания, т.е. если:
,
![]() ,
,
![]() .
.
Добротность контура при малых затуханиях:
![]() ,
,
![]() .
.
Заряд, напряжение, ток, энергия в колебательном контуре с сопротивлением.
Запишем для заряда конденсатора
.
Обычно затухание таково, что экспоненциальный множитель очень незначительно изменяется за достаточно большое число периодов затухающих колебаний.
Обозначим:
![]() .
.
Величина называется амплитудой заряда конденсатора затухающих колебаний.
Запишем для напряжения на обкладках конденсатора
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
амплитуда напряжения на конденсаторе.
-
амплитуда напряжения на конденсаторе.
Сила тока в цепи:
![]() ,
,
![]() ,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
- амплитуда силы тока в контуре.
Напряжение на сопротивлении
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
амплитуда напряжения на сопротивлении.
-
амплитуда напряжения на сопротивлении.
Энергия электрического поля
![]() .
.
Энергия магнитного поля
![]() .
.
Энергия электромагнитного поля (энергия контура)
.
Рассмотрим случай малого затухания
,
![]() ,
,
,

![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
где
![]() -
энергия контура в начальный (нулевой)
момент времени.
-
энергия контура в начальный (нулевой)
момент времени.
Апериодический режим в контуре с сопротивлением.
Запишем:
.
При величина становится мнимой, это означает, что колебательный процесс оказывается невозможным.
Запишем
,
![]() ,
,
![]() .
.
Обозначим
![]() .
.
Величина
![]() называется критическим сопротивлением.
называется критическим сопротивлением.
Колебания возможны (колебательный режим)
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Колебания невозможны (апериодический режим)
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Вынужденные электрические колебания.
Пусть в контуре действует гармоническое э.д.с.
![]() .
.
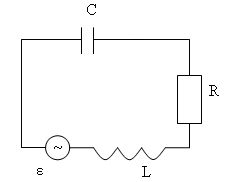
В этом случае дифференциальное уравнение имеет вид
![]() .
.
Решение уравнения имеет вид
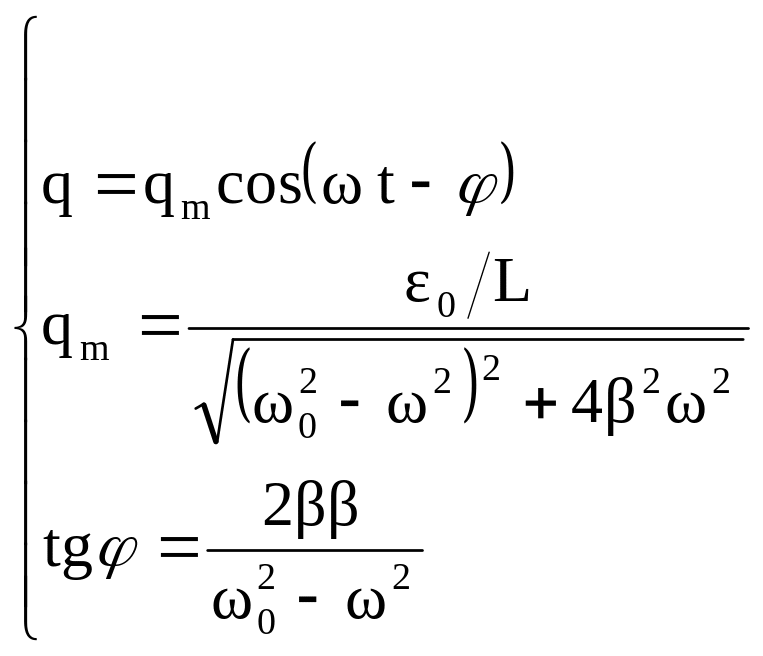
Очевидно,
![]() .
.
Резонанс в колебательном контуре.
Запишем для амплитуд
и
![]() :
:

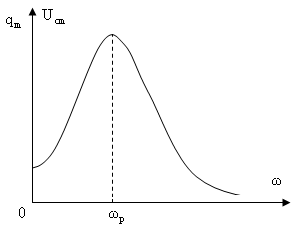
График зависимости
![]() и
и
![]() представлен на рисунке. Максимальное
значение амплитуд достигается при
резонансной частоте
представлен на рисунке. Максимальное
значение амплитуд достигается при
резонансной частоте
![]() ,
,
![]() .
.
Для амплитуд силы
тока и напряжения на сопротивлении:
![]() ,
,
![]()
 \
\

В этом случае
![]() .
.
Применение резонанса.
Пусть в колебательном контуре действует э.д.с.
![]()
Обозначим
![]() -
амплитуда напряжения на конденсаторе,
обусловленная действием эд.с.
-
амплитуда напряжения на конденсаторе,
обусловленная действием эд.с.
![]()
 .
.
Изменяя параметры контура можно добиться выполнения условий
![]() ,
,
![]() .
.
В этом случае
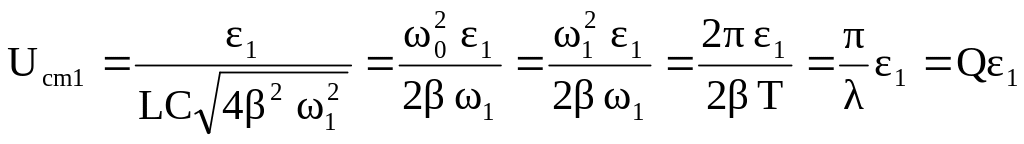 ,
,
![]() .
.
В случае малого затухания
![]() .
.
На конденсаторе
можно получить напряжение в
![]() раз превышающее
раз превышающее
![]() .
При этом напряжение, создаваемое
остальными э.д.с. будет очень малым. Тем
самым с помощью колебательного контура
можно выделять э.д.с необходимой частоты,
например, при настройке приемника.
.
При этом напряжение, создаваемое
остальными э.д.с. будет очень малым. Тем
самым с помощью колебательного контура
можно выделять э.д.с необходимой частоты,
например, при настройке приемника.
