Кинематика и динамика свободных гармонических колебаний.

Будем для определенности рассматривать пружинный маятник.

Дифференциальное уравнение колебаний имеет вид

,

,

,

.

Значение и можно найти из т.п. начальных условий, определяющих состояние системы в момент времени .

Скорость и ускорение грузика в проекции на ось .

,

,

,

,

,

.

Здесь - амплитуды скорости и ускорения грузика.

Проекция силы, действующей на грузик, на ось .

.

Сила называется возвращающей силой.

Кинетическая энергия маятника (грузика):

,

.

Потенциальная энергия упругой деформации пружины:

,

.

Полная энергия маятника

,

,

,

,

.

Полная энергия маятника, совершающего свободные гармонические колебания, остается постоянной.

Вектор – амплитуда.

Пусть частица совершает колебания вдоль оси . Положение равновесия частицы совпадает с началом оси . Частица совершает колебания по закону

.

построим окружность радиусом с центром в точке . Пусть некоторая точка движется по окружности как показано на рисунке с угловой скоростью равной . Проведем в точку радиус-вектор и обозначим его . Вектор вращается относительно точки с угловой скоростью .

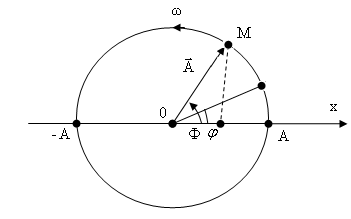
Проекция конца вектора на ось равна

,

,

.

Сравнивая видим, что колебательному движению частицы вдоль оси можно сопоставить вращательное движение вектора , который называется вектором – амплитудой. Модуль вектора – амплитуды равен амплитуде колебаний частицы . Начальное положение вектора – амплитуды таково, что угол между вектором и осью равен начальной фазе колебаний . Вектор – амплитуда вращается с угловой скоростью, равной круговой частоте колебаний частицы. Угол между вектором и осью в любой момент времени равен фазе колебаний частицы. Проекция вектора – амплитуды на ось в любой момент времени равна координате частицы, совершающей колебания вдоль оси .

Сложение гармонических колебаний.

Опыт дает, что если частица одновременно участвует в нескольких колебаниях, то смещение частицы равно геометрической сумме смещений, совершаемых частицей в каждом из колебаний, независимо от других.

П.1 Одинаково направленные колебания различной частоты.

Частица одновременно совершает два колебания вдоль оси

,

.

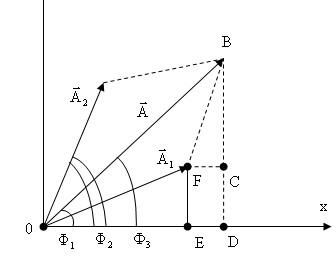
Этим колебаниям соответствуют векторы – амплитуды и , так что

,

,

,

.

Результирующее смещение частицы равно

.

Построим вектор , равный

.

Найдем проекцию на ось

,

.

Сравнивая видим, что результирующему колебанию частицы соответствует вектор – амплитуда

.

При этом

.

Будем искать и . Возведем в квадрат, запишем:

.

Далее:

,

.

Очевидно, что и не является гармонической функцией времени.

При сложении гармонических колебаний с разными частотами результирующие колебания не являются гармоническими.

п.2 Одинаково направленные колебания одинаковой частоты.

Пусть колебания происходят с одной и той же круговой частотой

,

,

,

,

, ,

,

,

, ,

.

При сложении одинаково направленных гармонических колебаний одинаковой частоты возникают гармонические колебания такой же частоты.

Когерентные колебания.

Колебания называются когерентными, если разность фаз колебаний не зависит от времени и остается постоянной.

Запишем

,

,

,

,

,

,

, ,

.

Колебания одинаковой частоты являются когерентными.

Сложение когерентных колебаний.

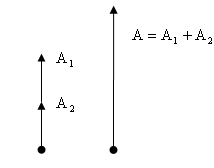
1.Синфазные когерентные колебания.

Колебания называются синфазными, если разность фаз колебаний кратна четному числу

,

Запишем

.

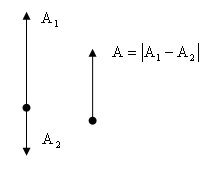
2. Колебания с противоположными фазами.

Колебания называются колебаниями с противоположными фазами (в противофазе), если разность фаз колебаний кратна нечетному числу

,

.

Биения.

Биениями называются колебания, возникающие при сложении двух одинаково направленных колебаний с близкими частотами. Разность частот колебаний называется частотой биений.

,

.

Рассмотрим случай

,

,

, ,

, .

Величина - круговая частота биений.

,

.

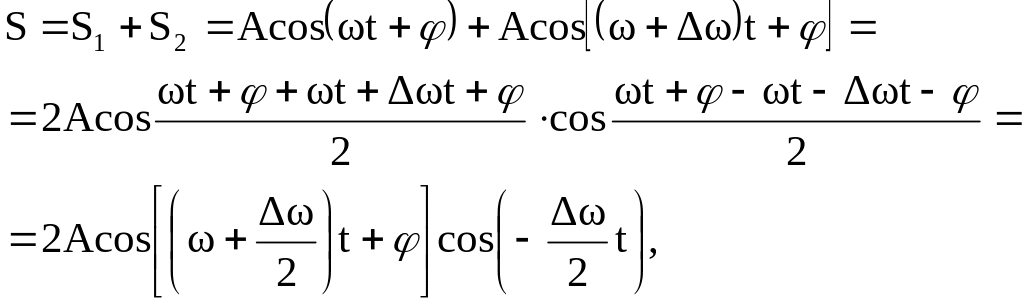
При выполнении условия

.

практически не изменяются во времени, равное периоду и имеет смысл амплитуды.

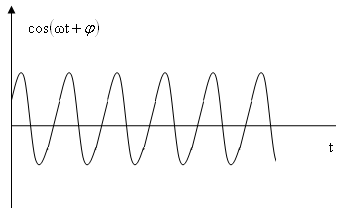
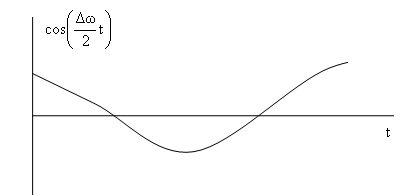
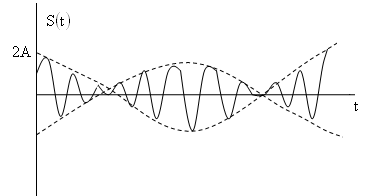
Амплитудой биений называется величина

.

График функции имеет следующий вид.