Излучение электромагнитных волн.

В соответствии с уравнением Максвелла для возникновения электромагнитной волны необходимо и достаточно, чтобы в некоторой точке пространства возникло изменяющееся со временем, например, электрическое поле, т.е.

Рассмотрим электрический диполь, в котором заряды связаны не жестко, а упруго, причем отрицательный заряд совершает колебания вблизи неподвижного положительного заряда .

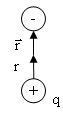
Дипольный электрический момент системы изменяется со временем по закону

напряженность электрического поля, создаваемого диполем пропорциональна дипольному электрическому моменту, следовательно:

Таким образом, диполь с дипольным моментом является источником переменного электрического поля и, следовательно, источником электромагнитной волны.

Обозначим - мощность, излучаемую диполем, т.е. энергию, излучаемую в единицу времени.

Расчеты дают, что

Запишем

где - ускорение отрицательного заряда диполя.

Из следует, что

в общем случае, всякий заряд , движущийся с ускорением излучает электромагнитные волны. Мощность излучения равна

Эффект Доплера для электромагнитных волн.

Пусть в системе отсчета , в ее начале находится приемник электромагнитного излучения. В начале системы отсчета находится источник электромагнитного излучения, покоящийся относительно .

Пусть система движется относительно системы с постоянной скоростью , направленной вдоль совпадающих осей как показано на рисунке. Источник излучает в направлении приемника плоскую электромагнитную волну с частотой .

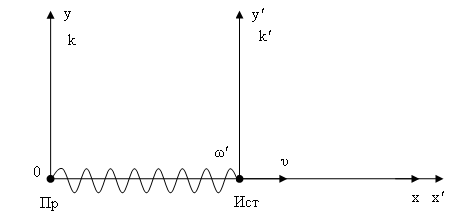
Уравнение волны в системе связанной с источником имеет вид

Согласно принципу относительности Эйнштейна все уравнения описывающие физические явления имеют одинаковый вид во всех инерциальных системах отсчета. Следовательно, уравнение плоской электромагнитной волны в системе имеет вид