
- •П.2 Математический маятник.
- •П.3 Физический маятник.
- •Свободные колебания.
- •Период и частота колебаний.
- •Кинематика и динамика свободных гармонических колебаний.
- •Вектор – амплитуда.
- •Сложение гармонических колебаний.
- •П.1 Одинаково направленные колебания различной частоты.
- •Взаимно перпендикулярные колебания.
- •Ангармонические (негармонические) колебания.
- •Свободные затухающие колебания.
- •Энергия затухающих колебаний.
- •Характеристики затухающих колебаний.
- •Апериодическое движение.
- •Дифференциальное уравнение для колебательного контура.
- •Свободные колебания в контуре без сопротивления.
- •Свободные затухающие колебания в контуре с сопротивлением.
- •Заряд, напряжение, ток, энергия в колебательном контуре с сопротивлением.
- •Переменный ток.
- •Мощность в цепи переменного тока.
- •Возникновение и распространение упругой волны.
- •Уравнение волны.
- •П.1 уравнение плоской гармонической волны.
- •П.2 Уравнение сферической гармонической волны.
- •П.3 Уравнение плоской гармонической волны, распространяющейся в произвольном направлении.
- •Волновое уравнение.
- •Скорость упругой волны в твердой среде.
- •Скорость упругой волны в газе.
- •Скорость упругой волны в однородном контуре.
- •Энергия упругой волны.
- •Плотность потока энергии.
- •Интенсивность волны.
- •Стоячие волны.
- •Узлы и пучности стоячей волны.
- •Поток энергии в стоячей волне.
- •Скорость упругой волны в однородном шнуре.
- •Колебания струны.
- •Эффект Доплера для звуковых волн.
- •Электрические волны.
- •Плоская электромагнитная волна.
- •Энергия электромагнитной волны.
- •Плотность потока энергии электромагнитной волны.
- •Интенсивность волны.
- •Импульс электромагнитной волны.
- •Давление электромагнитной волны.
- •Излучение электромагнитных волн.
- •Эффект Доплера для электромагнитных волн.
Плотность потока энергии электромагнитной волны.
Запишем
![]() ,
,
![]() .
.
В вакууме:
![]()
![]() .
.
Умножим и на скорость электромагнитной волны, получим
![]() ,
,
![]() .
.
С учетом направления векторов, запишем
![]() ,
,
![]() .
.
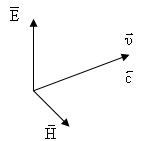
Величина в правой
части имеет смысл вектора плотности
потока энергии электромагнитной волны.
Обозначим этот вектор
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Вектор называется плотностью потока электромагнитной волны или вектором Пойнтинга.
Модуль плотности потока электромагнитной волны равен
![]() .
.
Направление вектора совпадает с направлением скорости электромагнитной волны.
Интенсивность волны.
Возьмем некоторую
произвольную поверхность
.
Поток энергии электромагнитной волны
через эту поверхность равен потоку
вектора
![]()
![]() ,
,
![]()
![]() ,
,
где
-
нормаль к элементу поверхности
![]() .
.

Найдем среднее за период значение потока энергии
 ,
,
![]() .
.
Возьмем плоский
участок поверхности
![]() ,
перпендикулярный скорости волны
.
Запишем для него из
,
перпендикулярный скорости волны
.
Запишем для него из
![]() .
.

Запишем
![]() ,
,
Величина в правой части имеет смысл энергии, переносимой в 1с в среднем за период через единичную площадку, перпендикулярную скорости электромагнитной волны.
Она называется интенсивностью электромагнитной волны.
,
 ,
,
![]() .
.
Импульс электромагнитной волны.
Плоская электромагнитная волна нормально падает на плоскую поверхность проводника. Выделим элемент проводника. Опыт дает, что волна при этом проникает на некоторую глубину и исчезает, т.е. поглощается.
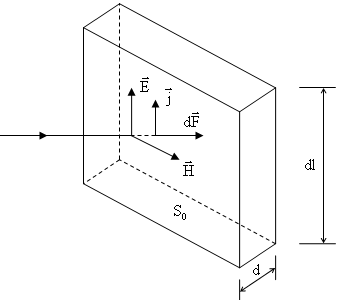
Электрическое поле волны приводит к появлению электрического тока, причем
![]() ,
,
![]() .
.
На ток со стороны магнитного поля волны действует сила Ампера
![]() ,
,
![]() ,
,
где - объем элемента.
Электрический ток совершает работу, которая идет на увеличение внутренней энергии элемента проводника
![]() ,
,
![]() .
.
Разделим
 ,
,
![]() .
.
Запишем для элемента проводника 2-й закон Ньютона
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() -
импульс, который получает элемент
проводника за время
в результате действия силы
-
импульс, который получает элемент
проводника за время
в результате действия силы
![]() .
.
Проинтегрируем по всей плоской поверхности проводника
![]() ,
,
![]() .
.
Здесь
![]() - модуль импульса, который получает
проводник за время
при падении на его поверхность
электромагнитной волны, энергия которой
- модуль импульса, который получает
проводник за время
при падении на его поверхность
электромагнитной волны, энергия которой
![]() .
Очевидно проводник может получить
импульс только от самой электромагнитной
волны.
.
Очевидно проводник может получить
импульс только от самой электромагнитной
волны.
Электромагнитная волна, падающая на поверхность проводника, поглощается в нем и при этом передает проводнику свой импульс, которым обладает, т.е. импульс электромагнитной волны равен
![]() .
.
Итак, электромагнитная волна с энергией обладает импульсом, модуль которого равен
![]() .
.
Энергию волны находим интегрированием
.
Продифференцируем по объему
![]() .
.
Обозначим
![]() ,
,
где
![]() - импульс электромагнитной волны в
единице объема пространства
- импульс электромагнитной волны в
единице объема пространства
![]() .
.
Запишем
![]() ,
,
![]() ,
,
![]() ,
,
где - вектор Пойнтинга.
Давление электромагнитной волны.
Запишем для элемента проводника на который нормально падает электромагнитная волна 2-й закон Ньютона
,
![]() ,
,
![]() ,
,
где
![]() -
импульс электромагнитной волны, падающей
в течение
на участок проводника
.
-
импульс электромагнитной волны, падающей
в течение
на участок проводника
.
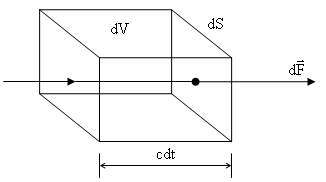
Выделим объем в
виде параллелепипеда с гранями
и ребром
![]() .
За время
волна дойдет от левой грани до грани
проводника
и поглотится. Следовательно,
.
За время
волна дойдет от левой грани до грани
проводника
и поглотится. Следовательно,
![]() ,
,
где
![]() -
объем параллелепипеда.
-
объем параллелепипеда.
![]() .
.
Сила действует перпендикулярно к , т.е. является силой давления на . Разделим на обе части
![]() ,
,
![]() .
.
Обозначим:
![]() -
давление,
-
давление,
![]() ,
,
![]() .
.
Пусть волна падает
под углом
![]() к нормали поверхности. В общем случае
к нормали поверхности. В общем случае
![]() ,
,
![]() .
.
- коэффициент отражения,
- полное поглощение,
![]() -
полное отражение.
-
полное отражение.

