2.3. Нормированное нормальное распределение (z).

Если Х – нормально распределенная случайная величина с параметрами m и σ, то величина также распределена нормально с параметрами и (кратко обозначают ).

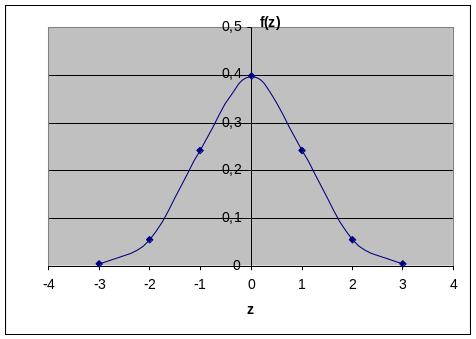
Плотность нормированного нормального распределения:

Кривая плотности распределения имеет вид:

2.4. Распределение к.Пирсона ( )

Если – нормально распределенные независимые случайные величины, причем математическое ожидание каждой из них , а среднее квадратическое значение , то сумма квадратов этих величин распределена по закону («хи»-квадрат) с степенями свободы, где z – число связей, наложенных на величины _.

Например, если величины связаны одним линейным соотношением , то число степеней свободы .

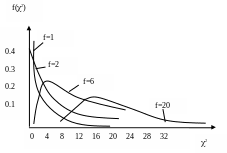
График плотности распределения закона для различных чисел степеней свободы имеет вид:

2.5. Распределение Стьюдента (t)

Если z – нормально распределенная случайная величина, причем и , а – независимая от z величина, которая распределена по закону с f степенями свободы, то величина

имеет распределение Стьюдента с f степенями свободы.

Распределение t определяется одним параметром – числом степеней свободы f.

С увеличением числа степеней свободы распределение быстро приближается к нормальному.

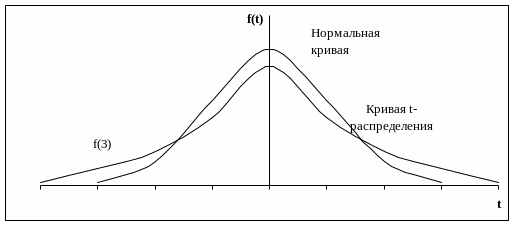
График плотности распределения t для имеет вид:

2.6. Распределение Фишера (f)

Если и - независимые случайные величины, распределенные по закону со степенями свободы f₁ и f₂ , то величина

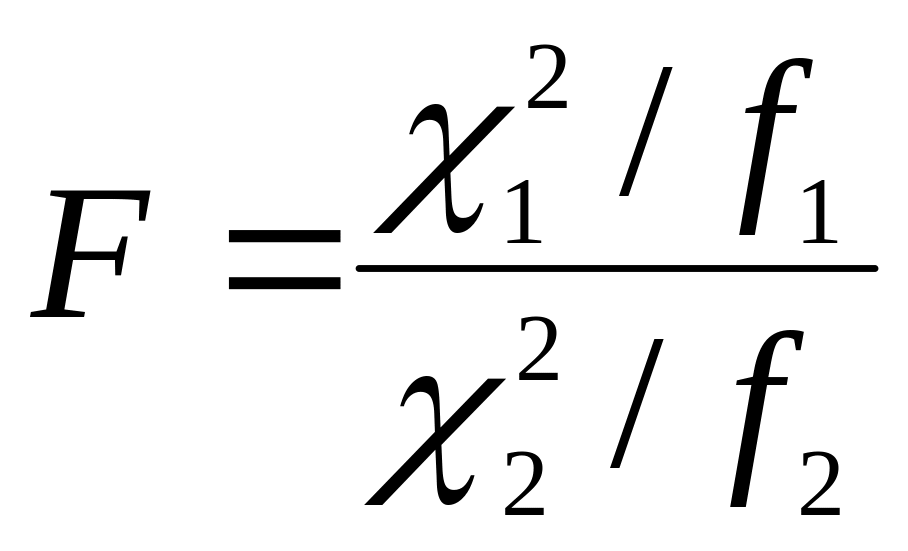
имеет распределение, называемое распределением Фишера со степенями свободы f₁ и f₂ .

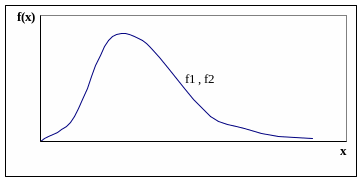
Распределение F определяется двумя параметрами – числами степеней свободы f₁ и f_2.

График плотности распределения F для чисел степеней свободы f₁ и f₂ представлен на рисунке:

Задача 2.3. По заданным параметрам распределений записать плотности распределений, построить кривые распределений, найти числовые характеристики, определить вероятность попадания значений случайной величины в интервал (α , β), т.е. :

а) нормальное распределение: , кратко обозначают N(-6 , 3).

Плотность нормального распределения

.

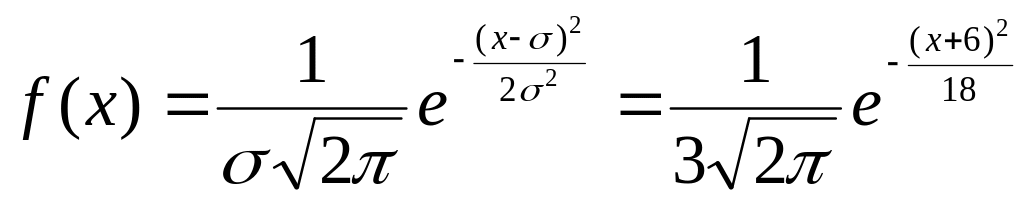Кривая нормального распределения симметрична относительно прямой , максимальное значение достигается при и равно

Точки перегиба:

;

Кривая нормального распределения (кривая Гаусса) имеет вид:

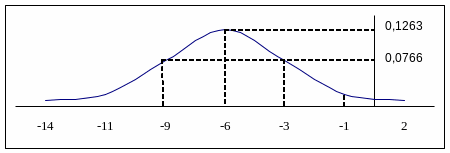
Определим теперь вероятность попадания значений случайной величины в заданный интервал (-1 ; 2):

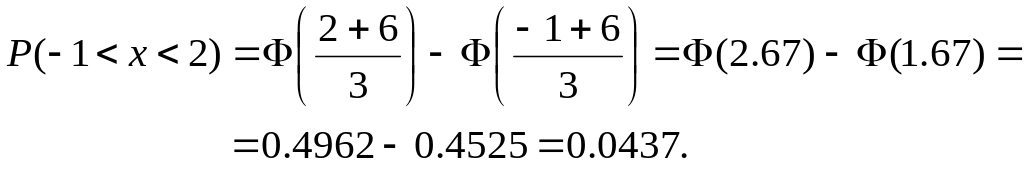
Это площадь заштрихованной области под кривой Гаусса от Х=-1 до Х=2.

Зная параметры, легко найти числовые характеристики:

; ;

б) показательное распределение: λ=1.6

Плотность показательного распределения для

.

Кривая плотности распределения имеет вид:

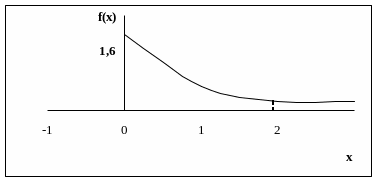
Определим Р(-1<х<2). Так как для х<0 f(х)=0, то надо взять интервал (0;2)

(площадь заштрихованной области).

Числовые характеристики этого распределения

;

в) равномерное распределение: а=-5; b=5.

Плотность равномерного распределения:

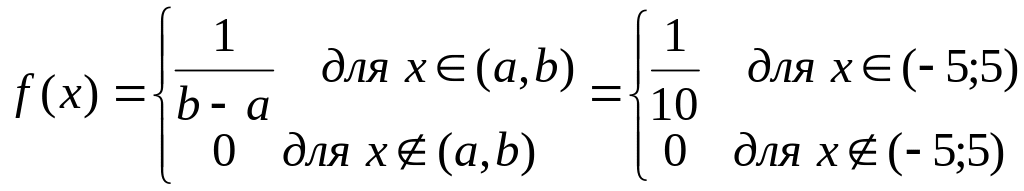
Кривая плотности:

.

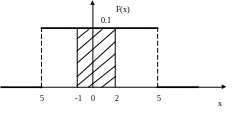
Числовые характеристики:

; .