
- •3. Основы квантовой статистики
- •3.1. Квантовый ансамбль микрочастиц
- •3.2. Фермионы и бозоны
- •3.3. Фазовое пространство. Плотность состояний
- •3.4. Распределение частиц по квантовым состояниям. Виды статистик
- •3.5. Применение статистики Ферми-Дирака к электронному газу в металлах
- •3.6. Приложение статистики Бозе-Эйнштейна к фотонному газу
3.5. Применение статистики Ферми-Дирака к электронному газу в металлах
Свободные электроны в металле можно считать невзаимодействующими частицами идеального газа. Аппроксимируя периодически изменяющуюся с координатой Х потенциальную энергию электрона в металле U(x) неким средним постоянным значением, металл можно представить как прямоугольную потенциальную яму для электронов, показанную на рис. 3.6 (см. также лекцию 5).
Поскольку электроны являются фермионами, то при абсолютном нуле температуры они будут последовательно заполнять квантовые состояния, а следовательно, и энергетические уровни. В соответствии с распределением Ферми-Дирака на каждом уровне может разместиться 0 или 1, или максимум 2 электрона с противоположными спинами. Если мы рассматриваем электроны в единице объема, то "последний" n-й электрон займет энергетический уровень, который и определит максимальную кинетическую энергию электронов в металле при Т = 0. Эта энергия, которая отсчитывается от дна потенциальной ямы и, следовательно, положительна, называется энергией Ферми ЕF(0) и определяет границу между заполненными и пустыми состояниями. Уровень Ферми ЕF для электронов играет роль уровня химического потенциала () для незаряженных частиц, и функция Ферми-Дирака записывается теперь следующим образом:
(3.24)

При абсолютном нуле из вида функции fФ-Д следует:
fФ-Д = 1 для E < EF;
fФ-Д = 0 для E > EF.
Другими словами, все состояния, лежащие ниже уровня Ферми, полностью заняты электронами, а выше него - свободны, что изображено на рис. 3.7 в виде ступенчатой функции. При любой T 0 fФ-Д = 0,5 для Е = ЕF, что отражает статистический смысл уровня Ферми: при любой температуре его заселенность равна 0,3.

Рис. 3.6. Заполнение энергетических уровней электронами в металле
Выражение для ЕF при Т = 0 легко найти из условия, что интегрирование числа частиц по веем возможным состояниям должно дать полное число частиц n в системе (при Vo = 1):
(3.25)
![]()
Подставляя полученные ранее выражения для g(Е) и fФ-Д = 1 получаем:
(3.26)
![]()
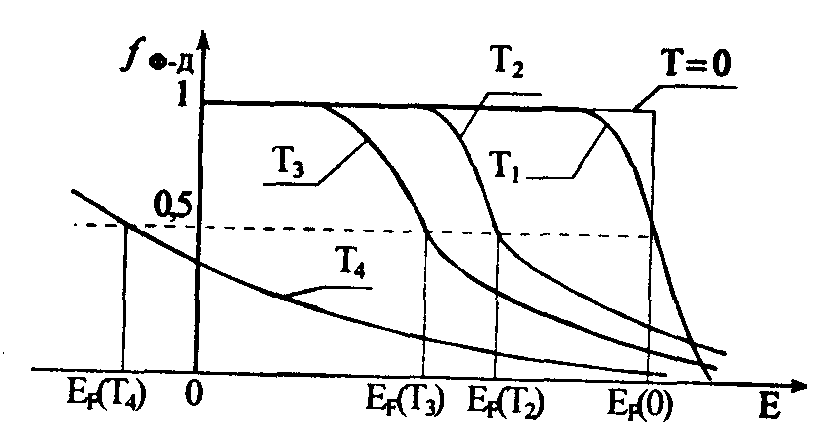
Рис. 3.7. Распределение Ферми-Дирака при различных температурах Т4 > Т3> Т2 > Т1 > 0
Таким образом, при Т = 0 величина химического потенциала (энергии Ферми) однозначно определяется концентрацией электронов. Зависимость ЕF(0) от n нелинейная, так как вследствие роста g(Е) на более высоких энергетических уровнях в данном интервале dЕ можно разместить больше электронов.
При увеличении Т часть электронов, лежащих ниже уровня Ферми, переходит в более высокие энергетические состояния за счет теплового возбуждения, освобождая состояния, лежащие ниже ЕF. В этом случае при не слишком высоких температурах Т, когда зависимостью ЕF(Т) можно пренебречь, функция распределения будет иметь вид, представленный на рис. 3.7. В области энергий, удовлетворяющих соотношению (Е – ЕF) >> kТ, выражение для fФ-Д переходит в классическую формулу Максвелла-Больцмана. Это и не удивительно, так как эти уровни очень слабо заселены (fФ-Д << 1), т.е. в этой области энергий число частиц много меньше числа возможных состояний, следовательно, квантовыми свойствами этой части электронов можно пренебречь и рассматривать их как невырожденный коллектив. При этом основная часть электронов остается совершенно нечувствительной к изменениям Т, чем объясняется тот факт, что при обычных температурах электроны практически не дают вклада в теплоемкость кристалла, поскольку тепловым возбуждением затронута лишь мизерная их часть в интервале kТ 2kТ вблизи ЕF.
Распространить теорию электронного газа на случай произвольных температур можно, используя условие:
(3.27)

которое позволяет определить температурную зависимость уровня Ферми даже в области температур, где электронный газ нельзя считать ни классическим (невырожденным), ни квантовым (вырожденным).
Однако практический интерес представляют именно предельные случаи: сильно вырожденное состояние, что соответствует всем металлам, вплоть до температуры их плавления, и невырожденное состояние, описывающее ситуацию во многих полупроводниках.
Сильное вырождение электронного газа
имеет место в металлах даже при достаточно
высоких температурах (в несколько тысяч
Кельвин), поскольку при типичной плотности
электронов около 1022 см-3
расчет по формуле (3.26) дает значение
ЕF(0) в несколько
электрон-вольт (например, 5,5 эВ - для Аg,
4,7 эВ - для Li, в то время
как, например, при Т = 5000 К величина kТ
0,4 эВ). Таким образом,
для всех значений энергии вне области
2 3kТ
влево от ЕF (cм.
рис. 3.7)
![]() ,
т.е. fФ-Д
1 и практически все состояния заняты
электронами.
,
т.е. fФ-Д
1 и практически все состояния заняты
электронами.
Использование уравнения (3.27) приводит при условии kТ << ЕF к следующему выражению для энергии уровня Ферми, отсчитываемой от дна потенциальной ямы металла:
(3.28)

Из этого выражения следует, что с ростом температуры (а также с уменьшением концентрации электронов) уровень Ферми смещается по шкале энергий влево, однако, его заселенность по-прежнему остается равной 0,5 (см. рис. 3.7). Кроме того, с ростом Т функция fФ-Д в области ЕF все более растягивается, т.е. происходит все более интенсив-ное изменение заселенности энергетических уровней.
Следует отметить, что в реальных условиях изменение ЕF с увеличением температуры весьма мало. Например, согласно (3.28), для Аg, имеющего ЕF(0) = 5,5 эВ даже при температуре плавления, равной 1250 К (kТ 0,1 эВ), изменение энергии Ферми (ЕF(0) – ЕF) составляет лишь около 0,03 % от ЕF(0).
При высоких температурах и низких концентрациях, при которых длина волны де Бройля электронов будет значительно меньше среднего расстояния между частицами, влиянием принципа Паули на функцию распределения можно пренебречь: электронный газ становится невырожденным, т.е. ведет себя как классический. Критерием невырожденности может являться малая заселенность практически всех энергетических состояний: fФ-Д << 1, и, следовательно:
(3.29)
![]()
Поскольку соотношение (3.29) должно
выполняться при любых Е, то это означает,
что
![]() ,
т.е. ЕF << -
kТ. Таким образом, химический
потенциал (энергия уровня Ферми)
невырожденного газа должен быть
отрицательным.
,
т.е. ЕF << -
kТ. Таким образом, химический
потенциал (энергия уровня Ферми)
невырожденного газа должен быть
отрицательным.
Часто вводят понятие температуры вырождения, равной температуре электронов на уровне Ферми ТF = ЕF/k, так что при Т > ТF электронный газ становится невырожденным. Оценка показывает, что ТF для металлов составляет несколько десятков тысяч Kельвин при температуре их плавления около 1000 К, т.е. газ свободных электронов в проводниках всегда вырожден.
Распределение числа электронов по энергетическим состояниям при произвольной температуре, которое необходимо знать для объяснения таких свойств металлов, как электропроводность, теплоемкость и т.д., задается выражением:
(3.30)
![]()
и представлено на рис. 3.8.

Рис. 3.8. Зависимость средней заселенности состояний (fФ-Д),
плотности числа состояний (g) и числа электронов в единичном интервале энергий (dn/dE) для электронов в металле от энергии
Резюмируем основные результаты рассмотренного выше применения статистики Ферми для описания электронного газа в металлах.
Свободные электроны, образующие в металлических (и полупроводниковых) кристаллах электронный газ, по своим свойствам отличны от молекул идеального газа. Поэтому и законы статистического распределения этих частиц оказываются также различными: идеальный газ подчиняется статистике Максвелла - Больцмана, а электронный газ - квантовой статистике Ферми-Дирака. Для уяснения различия между этими статистиками сравним исходные положения, на которых они построены.
1. Статистика Максвелла - Больцмана имеет дело с частицами, движение которых строго подчиняется законам классической механики. Состояние любой такой частицы однозначно определяется заданием ее координат х, у, z и составляющих импульса рx, ру, рz. Как координаты, так и импульсы могут меняться непрерывно. Поэтому возможны состояния, бесконечно мало отличающиеся друг от друга координатами, импульсами и энергиями. Эти состояния классическая статистика считает различными.
Электроны, образующие электронный газ, обладают волновыми свойствами, и их движение описывается волновым уравнением Шредингера. Следствием этого является тот факт, что энергия и другие характеристики движения электрона в твердом теле становятся квантованными: они могут принимать лишь строго определенные значения. Каждое такое значение соответствует определенному квантовому состоянию электрона в твердом теле.
Наличие у электрона волновых свойств исключает возможность различать два состояния х, у, z, рx, ру, рz. и х+dх, у+dу, z+dz, рx+dрx, ру+dрy,, рz+dрz, если произведение dхdуdzdрxdруdрz оказывается меньше h3 (соотношения неопределенностей):
(3.31)
где h - постоянная Планка. Так как произведение dхdуdzdрxdруdрz представляет собой элемент 6-мерного фазового пространства d, то из соотношения (3.31) следует, что различным элементам фазового пространства d будут соответствовать различные квантовые состояния электрона лишь в том случае, если размер этих элементов не меньше h3. Поэтому в квантовой статистике за элементарную ячейку 6-мерного фазового пространства принимается
d = h3. (3.32)
При рассмотрении свободных электронов предполагается, что их потенциальная энергия одинакова во всех точках металла, вследствие чего распределение в объеме V является равномерным. В этом случае вместо 6-мерного фазового пространства X, Y, Z, Px, Py, Pz пользуются 3-мерным пространством импульсов Px, Py, Pz и разбивают его на элементарные ячейки размером
(3.33)
d = h3/V. (5.32)
Каждой такой ячейке соответствует отдельное квантовое состояние, отличимое от других состояний.
Таким образом, первое отличие квантовой статистики от статистики Максвелла-Больцмана состоит в методе деления фазового пространства на элементарные ячейки. Классическая статистика не делает никаких ограничений на величину этих ячеек, полагая, что они могут быть сколь угодно малыми. Квантовая же статистика считает, что физический смысл имеют лишь ячейки размером не менее h3 для 6-мерного фазового пространства и h3/V для 3-мерного пространства импульсов.
2. Электроны подчиняются принципу Паули. Согласно этому принципу в твердом теле в каждом квантовом состоянии с энергией Е может находиться не более 2-х электронов, отличающихся друг от друга направлением спинов. Это означает, что каждая ячейка h3/V пространства импульсов, соответствующая данному квантовому состоянию, может вместить не более 2-х электронов.
3. Статистика Максвелла-Больцмана индивидуализирует молекулы газа, считая, что их можно (по крайней мере, принципиально) отличать друг от друга. Поэтому перестановка местами двух молекул идеального газа, находящихся в разных состояниях, приводит, согласно классической статистике, к новому микросостоянию системы. Квантовая же статистика Ферми-Дирака считает все частицы тождественными друг другу (неотличимыми друг от друга). Поэтому перестановка их местами не приводит к появлению нового микросостояния.
