3.3. Фазовое пространство. Плотность состояний

Поскольку состояние частицы определяется заданием трех коор­динат x, y, z и трех проекций импульса на оси координат p_x, p_y, p_z (с той или иной точностью), то удобно это состояние изображать в так называемом фазовом пространстве, т.е. в шестимерном пространстве с осями координат X, Y, Z, P_x, P_y, P_z. В классическом случае точные значения всех координат и проекций импульса могут быть определены одновременно, поэтому со­стояние частицы в этом случае изображается точкой в фазовом пространстве, а набор возмож­ных состояний будет сплош­ным. Перемещаясь во времени по непрерывному ряду состоя­ний в фазовом пространстве, классическая частица описыва­ет фазовую траекторию.

На рис. 3.1 приведены фазо­вые траектории классической частицы, совершающей некото­рые виды движения вдоль оси X:

• равномерное движение x = v_xt; v = const(t): p_x = const(x);

• равноускоренное движение с ускорением a(v_t=0 = 0) x = at²/2;

• гармоническое колебание под действием квазиупругой силы , где Е - полная энергия колебательного движения.

Фазовыми траекториями будут эллипсы , которые одновременно являются и кривыми равных энергий.

Если вблизи некоторой точки фазового пространства координа­ты и проекции импульса частицы могут изменяться в пределах x, x + x, …, p_x, p_x + p_x , … , то величина  = xyzp_x p_y p_z назы­вается ячейкой (элементом) фазового пространства,  = _v _p, где _v - объем ячейки в геометрическом пространстве; _p – в пространстве импульсов.

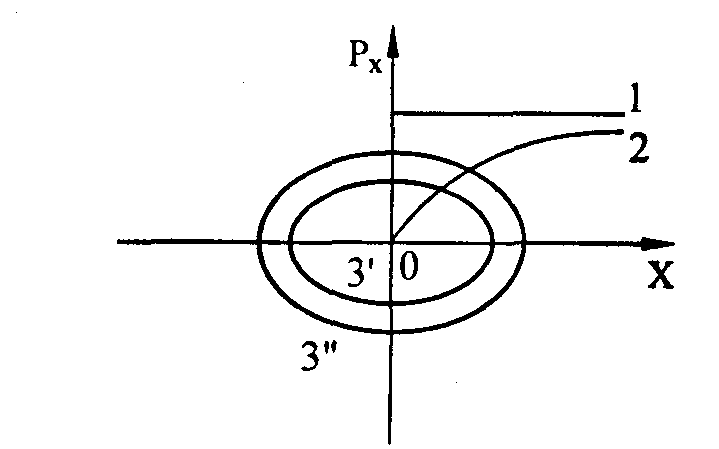
Рис. 3.1. Двумерное фазовое пространство. Фазовые траектории материаль­ной точки

при ее равномерном (1), равноускоренном (2) и гармониче­ском движении (кривые 3', 3" соот­ветствуют разным значениям пол­ной энергии)

Разница между коллективами классических и квантовых объектов проявляется, прежде всего, в конечности числа состояний, в которых мо­жет находиться микрочастица, движущаяся в ограниченной области фазо­вого пространства. Конечность же числа состояний следует непосредст­венно из соотношения неопределенностей, которое накладывает ограни­чение на максимальную точность одновременного определения коорди­наты и импульса. Действительно, два состояния микрочастицы с импуль­сами p₁ и p₂ в случае одномерного движения частицы вдоль оси Х на участ­ке длиной x могут быть различимы только в том случае, если p₁ – p₂ = p будет, по крайней мере, равно значению неопределенности по импульсу, задаваемому соотношением неопределенностей, т.е. p = h/x. Таким образом, для одномерного случая одному состоянию в фазовом про­странстве соответствует так называемая элементарная ячейка разме­ром h (фазовое пространство в этом случае двухмерно, и h определяет элементарную площадку в этом пространстве). Тогда число возмож­ных состояний микрочастицы Z = /x.p_x, где  - объем фазово­го пространства, соответствующий изменению ее импульса и координат в интервале , а (рис. 3.2,а). Тогда в трех­мерном пространстве импульсов:

Перемножив эти неопределенности импульса по координатам, по­лучаем неопределенность в определении величины вектора импульса: , т.е. величину объема элементарной ячейки импульсного пространства, соответствующего квантовому состоянию (см. рис. 3.26). Действительно, чтобы отличить два состояния микро­частицы с импульсами и нужно, чтобы векторы и попа­дали в разные ячейки фазового пространства. В противоположном случае импульсы неотличимы, так как разница их значений лежит в пределах точности измерения ( и на рис. 3.26).

Здесь следует отметить, что с учетом спина микрочастицы на эле­ментарную ячейку фазового пространства приходится не одно, а (2s + 1) состояний, где s - спиновое число микрочастицы.

Таким образом, если частицы находятся в ограниченном объеме фазо­вого пространства, то из конечности объема элементарной ячейки непо­средственно следует конечность числа состояний, в которых может нахо­диться микрочастица (т.е. она может обладать конечным набором воз­можных значений импульса и энергии). При этом число состояний, в которых может находиться микрочастица в определенном интервале изме­нения импульса (или энергии) зависит от значений импульса (или энер­гии). Другими словами, можно ввести понятие плотности числа состояний в импульсном (или энергетическом) пространстве, т.е. функцию g, пока­зывающую, сколько состояний находится в единичном интервале измене­ния импульса (энергии) вблизи данного значения импульса (энергии).

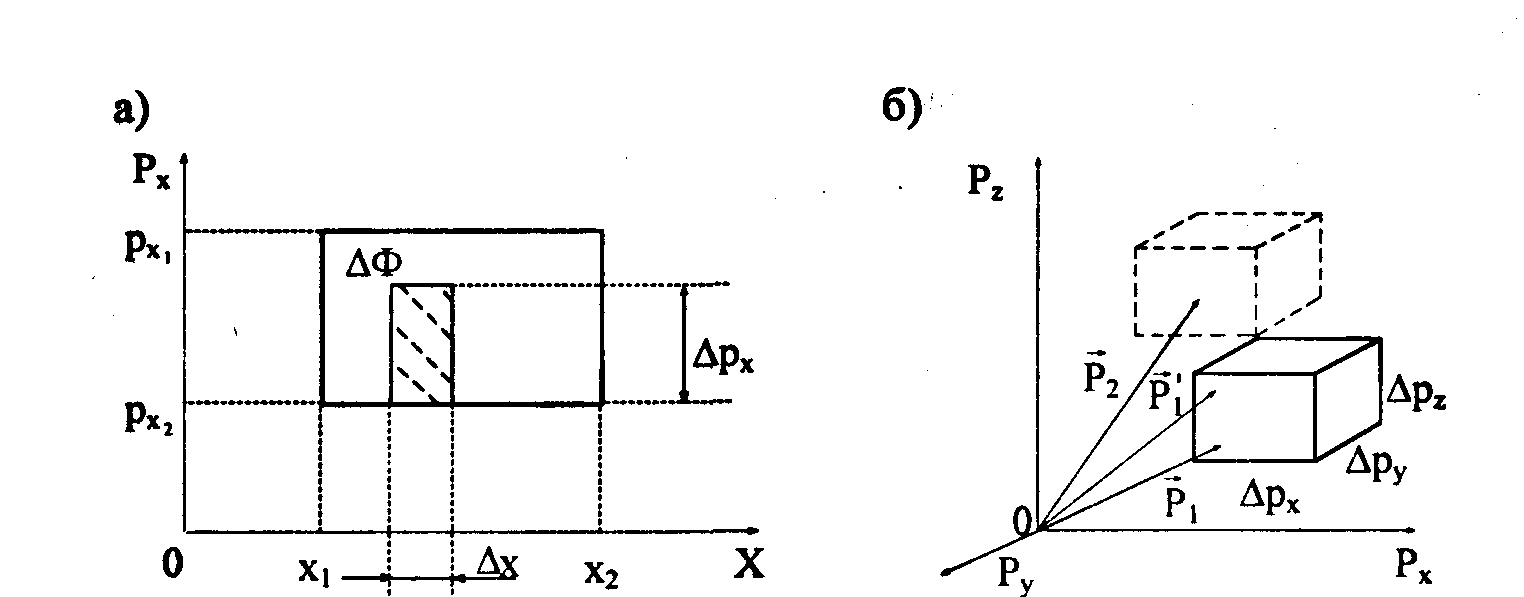
Рис. 3.2. Элементарная ячейка двухмерного фазового пространства импульс-координата

для одномерного движения (а) и ячейки трехмерного фа­зового пространства импульсов (б)

Чтобы получить выраже­ние для плотности числа со­стояний микрочастицы, дви­жущейся свободно в объеме V₀, рассмотрим в импульсном пространстве шаровой слой, заключенный между сферами с радиусами р и p + dp, объем такого слоя равен 4p²dp (см. рис. 3.3). Для того чтобы оп­ределить число состояний в шаровом слое, нужно объем слоя разделить на объем элементарной ячейки фазового пространств и, кроме того, для учета спиновых состояний умножить на (2s + 1). Таким образом, число возможных состояний, находящихся в интервал изменения импульса от р до p + dp, дается выражением

(3.6)

где - объем ячейки в пространстве импульсов.

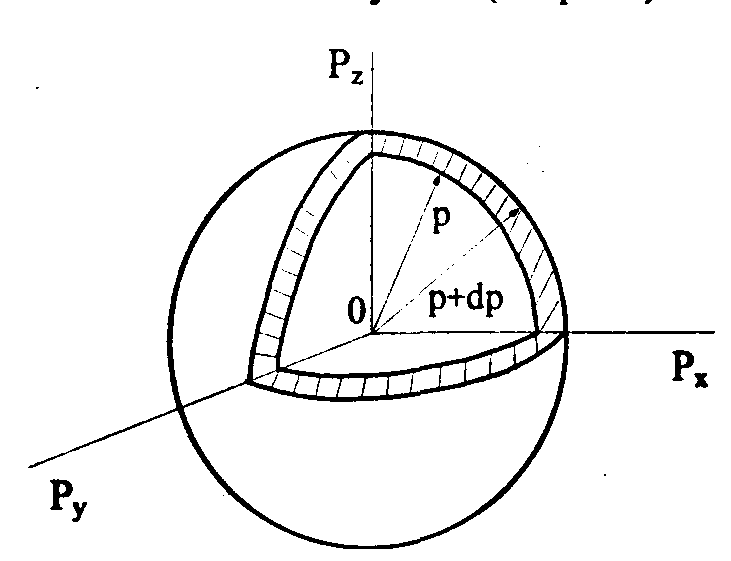
Рис. 3.3. К расчету плотности числа состояний

Для того чтобы получить выражение для плотности числа состоя­ний g(р) для единицы объема, надо разделить Z(р) на dр и V_о:

(3.7)

Для получения плотности числа состояний в энергетическом про­странстве g(Е) предположим, что микрочастицы являются квазисвободными, т.е. связь между энергией и импульсом имеет вид:

(3.8)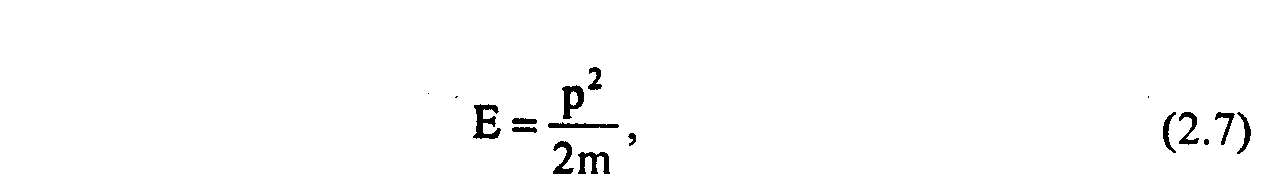

где m - масса частицы (в случае электронов в твердом теле под m подразумевается их эффективная масса).

Подставив выражения p² = 2mE; в формулу для Z(р) и разделив на dЕ, имеем:

(3.9)

Эта формула дает число состоя­ний в единичном интервале энергий около энергии Е и единичном объ­еме; график соответствующей зави­симости приведен на рис. 3.4. Об­щее число состояний в интервале dЕ равно g(Е)dЕ.

Рис. 3.4. Зависимость плотности числа состояний от энер­гии