Надстройки.

При решении инженерных задач широко используются различные надстройки Microsoft Excel.

Надстройки – это специальные средства, расширяющие возможности приложения EXCEL.

Перед решением задач этого класса необходимо активизировать надстройки Поиск решения или Подбор параметра.

Для подключения той или иной надстройки Excel необходимо выполнить следующую команду: меню Сервис\Надстройки и в появившемся окне активизировать необходимую надстройку.

V. Пример реализации итерационных методов решения

нелинейных уравнений с использованием электронных таблиц Мicrosoft Excel.

Приближенные методы решения нелинейных уравнений, такие как метод деления отрезка пополам (дихотомии), касательных, хорд хорошо реализуются в среде Microsoft Excel. Порядок решения этой задачи рассмотрим на примере решения нелинейного уравнения.

Пример. Решить нелинейное уравнение

, (5.1)

используя различные приближенные методы (касательных, хорд, дихотомии).

5.1. Первый этап – этап отделения корней.

На этом этапе необходимо определить количество действительных корней и локализовать их. Для этого протабулируем функцию и построим ее график, рис.6.

В соответствии с заданием (рис.1) выделим отрезок [a, b], на котором наша функция имеет единственную точку пересечения с осью Х, т.е. уравнение (5.1) имеет единственный корень.

Последовательность действий.

1. Подготовьте таблицу, как показано на рис.6.

Рис.6

В ячейки В1 и В2 введите значения начала и конца отрезка [a, b], предварительно определив область допустимых значений функции (ОДЗ). В нашем случае a=0,5 и b=3. В дальнейшем, если вы измените содержимое этих ячеек, Excel автоматически скорректирует таблицу табулирования и график функции в соответствии с новыми значениями [a, b].

2. В ячейку В3 введите шаг табулирования .

3. В ячейку A6 введите значение a, А6=В1.

4. Последующие значения узлов вычислите по формуле . Для этого введите формулу А7= А6+$B$3 и скопируйте эту ее вниз до х=3.

5. В ячейке В6 вычислите значение функции: т.е. и скопируйте эту формулу вниз до конца таблицы.

6. Используя мастер Диаграмм, постройте график функции, предварительно выделив блок ячеек А5:В16 (т.е. захватив заголовок таблицы).

Поскольку производная нашей функции существует и не изменяет знак для x[0,5, 3], то анализ таблицы и графика функции (рис.6) показывает, что на отрезке [0,5, 3] уравнение (5.1) имеет единственный корень.

5.2. Второй этап- этап уточнения корня с заданной точностью .

Метод Ньютона (касательных).

Исходя из начального приближения x₀, удовлетворяющего условию

f(x₀) f ^’’ (x₀)>0, (5.2)

корень x^* уравнения (5.1) с заданной точностью ε вычисляется по формуле

. (5.3)

Поскольку вторая производная положительна на отрезке [0,5; 3] (это видно и из графика функции), то в качестве нулевого приближения выберите x₀ =3, для которого выполняется условие (5.2).

Последовательность действий.

1. Подготовьте таблицу, как показано на рис.7.

2. В ячейку Е3 введите значение ε.

3. Используя автозаполнение введите номер итерации n в столбце А.

4. В ячейку В7 введите значение x₀, т.е. запишите формулу: В7=D2.

5. В ячейки C7, D7, E7 введите формулы для вычисления значений функции y=f(x), ее производной и абсолютной величины функции соответственно:

C7=B7*Ln(B7)-1, D7=Ln(B7)+1, E7=ABS(C7)

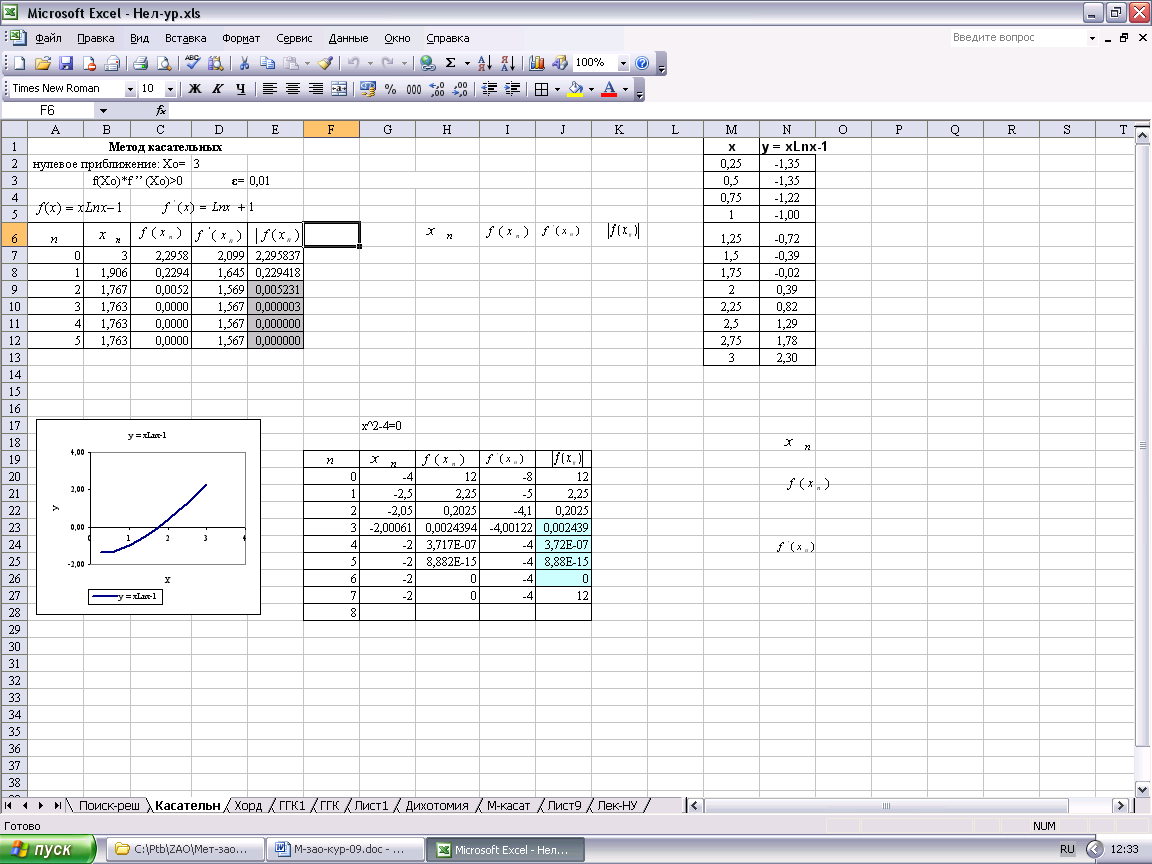
Рис.7.

6. В ячейку B8 введите формулу (5.3) для вычисления 1-го приближения: B8=B7-C7/D7.

7. Скопируйте ячейки C7, D7, E7 на строку ниже, т.е. соответственно в C8, D8, E8 и вы получите значения функции, ее производной и значение абсолютной величины функции в точке первого приближения х₁ .

8. Выделите блок ячеек В8:Е8 и скопируйте их вниз до конца таблицы.

9. Итерационный процесс следует продолжить до тех пор, пока не выполнится условие

, (5.4)

Тогда за приближенное решение уравнения (5.1) с точностью ε принимается n-я итерация, т.е.

Условное форматирование.

Чтобы сделать наглядным окончание итерационного процесса воспользуйтесь Условным форматированием. Для этого выделите блок ячеек Е7:Е12, и выполните команду меню Формат\Условное форматирование,

в открывшимся окне сделайте установки, как показано на рис.8. Цвет заливки определите, нажав кнопку Форомат.

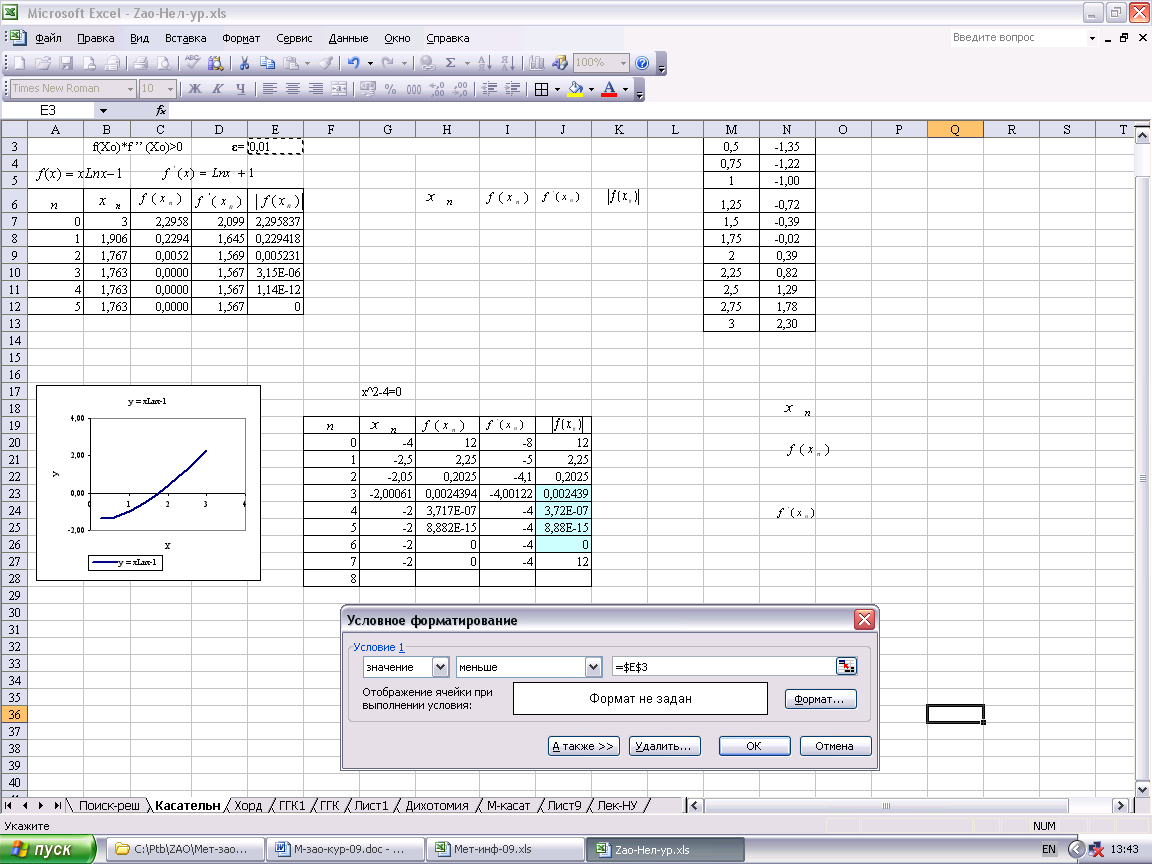
Рис.8.

Результат такого форматирования виден на рис.7. Ячейки столбца Е, значения которых удовлетворяют условию (5.4) тонированы.

Таким образом, за приближенное решение уравнения (5.1) с заданной точностью ε =0,01 по методу касательных принимается 2-я итерация, т.е. x^*1,767.

Измените значение ε, т.е. содержимое ячейки Е3, и вы увидите как изменится значение корня нашего уравнения. Проанализируйте результаты и вы получите ответ на пункт задания 5.2.

Метод хорд.

Исходя из начального приближения x₀, удовлетворяющего условию

f(x₀) f ^’’ (x₀)<0, (5.5)

корень x^* уравнения (5.1) с заданной точности ε вычисляется по формуле

. (5.6)

или

, (5.7)

В нашем случае условие (5.5) выполняется для х₀=а=1 (см.рис.6). Поэтому для построения итерационного процесса используем формулу (5.7).

Порядок решение аналогичен предыдущему методу касательных, поэтому рекомендуется внимательно ознакомиться с материалом пункта 5.1. Расчетная схема метода хорд приведена на рис.9.

За приближенное решение уравнения (5.1) по методу хорд с заданной точностью ε=0,01 принимается 4-я итерация, т.е. x^* 1,7618.

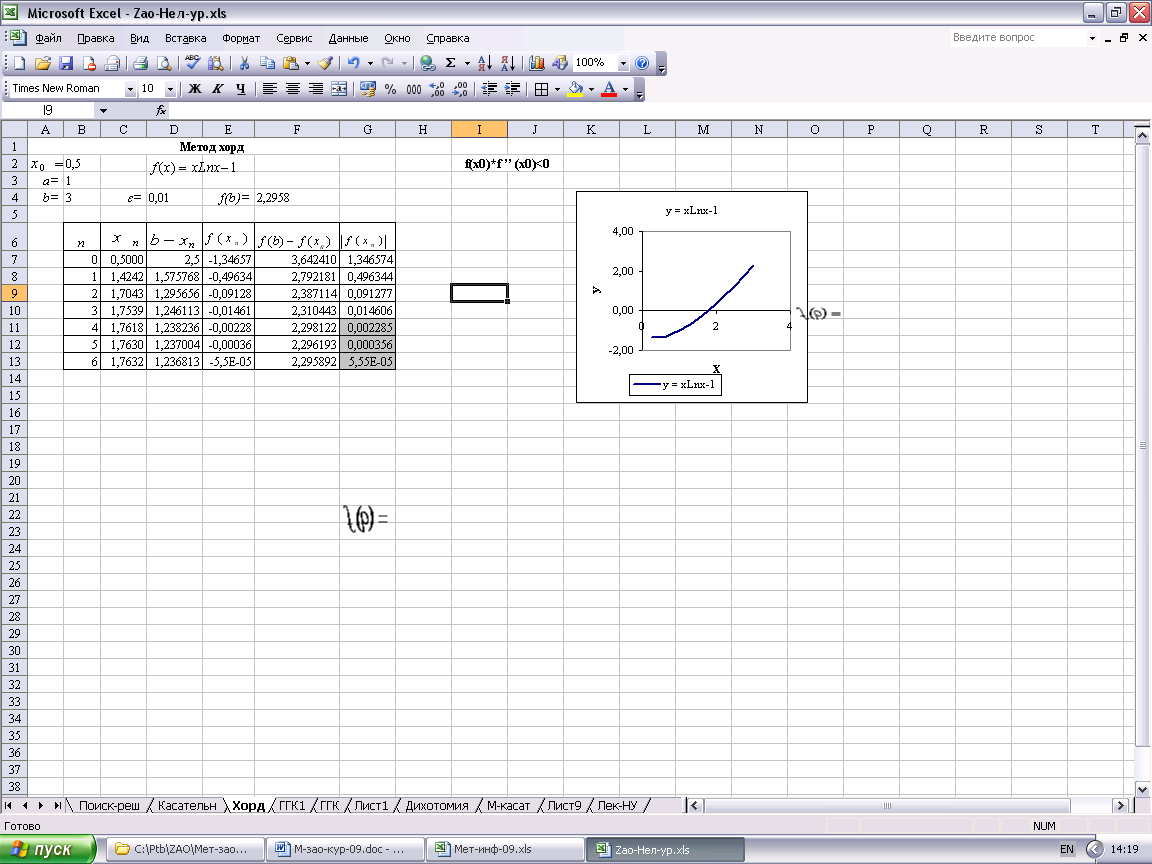
Рис.9.

Измените значение ε, т.е. содержимое ячейки D4, и вы увидите, как изменится значение корня нашего уравнения. Проанализируйте результаты и вы получите ответ на пункт задания 5.2.

Метод половинного деления (дихотомии).

Делим отрезок [a, b] пополам. Из двух отрезков [a, (a+b)/2] и [(a+b)/2, b] выбираем тот, на концах которого функция f(x) имеет разные знаки. Новый, уменьшенный вдвое, отрезок называем тем же именем [a, b] и снова делим пополам. Продолжая этот процесс, получим систему вложенных друг в друга отрезков.

Деление отрезков продолжаем до тех пор, пока длина последнего не станет меньше заданного ε, т.е. до тех пор, пока не выполнится условие:

. (5.8)

Тогда за приближенное решение уравнения (5.1) с точностью ε принимается

Последовательность действий.

1. Подготовьте таблицу, как показано на рис.10.

2. В ячейки В3, В4 введите значения a, b, а в ячейку D4 – значение ε.

3. Заполните первую строку таблицы:

• С7=В3, D7=B4;

• E7=C7*Ln(C7)-1, для вычисления f(a);

• аналогично в ячейки F7, G7, H7, I7 запишите формулы для вычисления f(b), x_n, f(x_n), .

4. В ячейки С8, D8 запишите формулы для формирования концов вложенных отрезков (т.е. значений a и b), используя функцию ЕСЛИ:

• C8=ЕСЛИ(H7*F7<0; G7; C7);

• D8=ЕСЛИ(H7*F7>0; G7; D7).

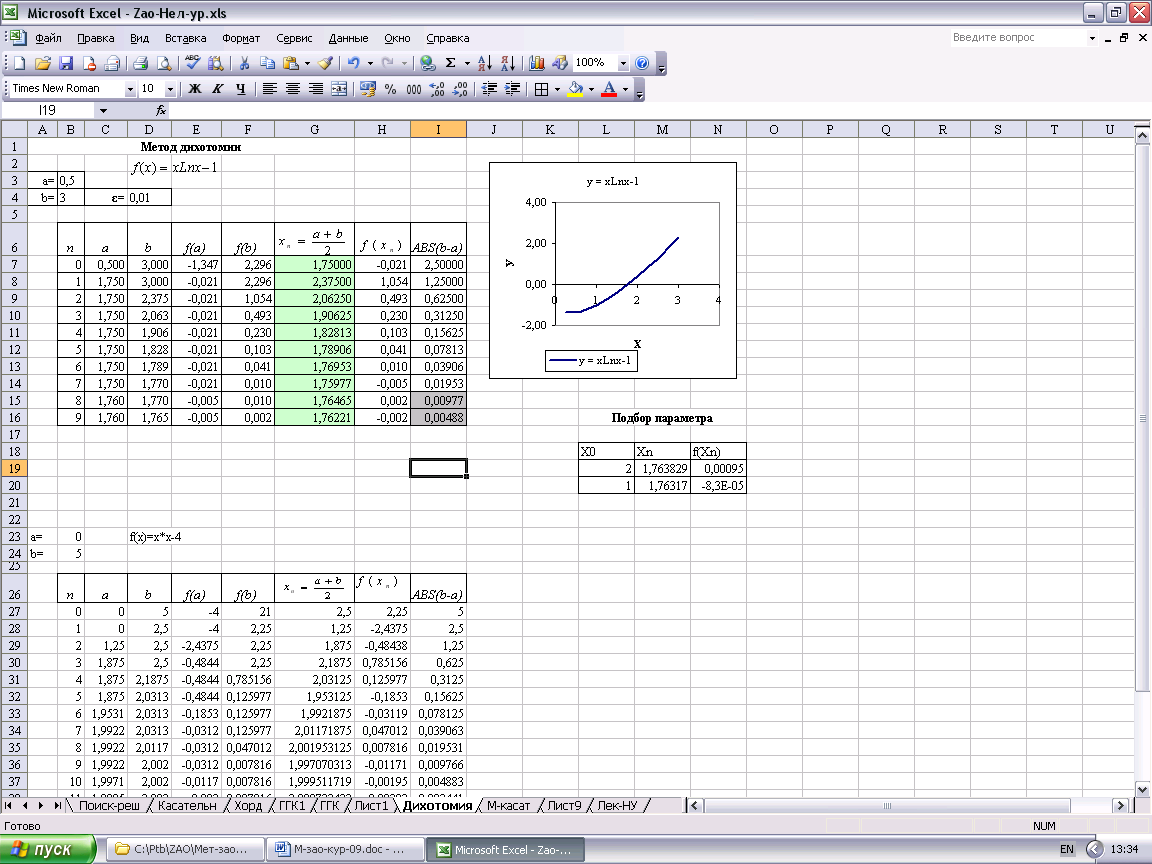
Рис.10.

5. Выделите ячейки E7:I7 и скопируйте их вниз на одну строку.

6. Выделите ячейки С8:I8 и скопируйте их вниз до конца таблицы.

Чтобы сделать наглядным окончание итерационного процесса, т.е. определить номер итерации для которой выполнится условие (5.8), воспользуйтесь Условным форматированием.

Использование Условного форматирования в ячейках I7:I16 наглядно демонстрирует ход итерационного процесса. Из рис.10 видно, что за приближенное решение уравнения (5.1) по методу дихотомии с заданной точностью ε =0,01 принимается 8-я итерация, x^* 1,7646

Измените значение ε, т.е. содержимое ячейки D4, и вы увидите, как изменится значение корня нашего уравнения. Проанализируйте результаты и вы получите ответ на пункт задания 3.1.2.